Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2007-08-19 23:16:21
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Geometry problem
Heres a geometry problem Ive just made up by myself. ![]()
Let O be a fixed point. Let Q be a variable point such that the length of OQ is less than or equal to 2a, where a is a fixed positive real number. Now let P and R be points satisfying the following conditions:
(i) OQPRO is a rectangle.
(ii) If PQ is shifted parallel to itself to P′Q′ such that P′Q′ and PR mutually bisect each other, then PP′RQ′P is a rhombus with sides of length a.
Prove that the locus of P is a circle of radius 2a.
Im sure it works. Still, if you find any problem with my problem, do let me know. ![]()
Last edited by JaneFairfax (2007-08-19 23:20:35)
Offline
#2 2007-08-21 13:05:32
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Geometry problem
Here are six red points.
Is that what you mean?
I only used up 279 bytes
on that small pic!!
The lower-center red dot
is Q prime, unmarked as such.
igloo myrtilles fourmis
Offline
#3 2007-08-21 23:42:40
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Geometry problem
Thats right. I should have provided a diagram anyway, so here it is.
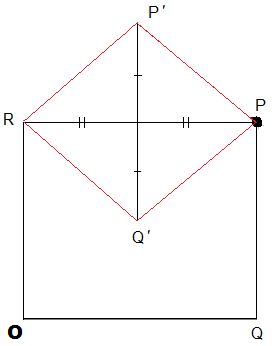
|P′Q′| = |PQ|
|PP′| = |P′R| = |RQ′| = |Q′P| = a
|OQ| ≤ 2a
Note that P can be below OQ as well, and that Q can also be to the left of O. Indeed, Q can be anywhere within a distance of 2a of O but for the purpose of analysis, we can assume WLOG that OQ is horizontal.
Last edited by JaneFairfax (2007-08-21 23:52:07)
Offline
#4 2007-08-23 23:55:49
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Geometry problem
Offline
#5 2007-08-27 08:59:48
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Geometry problem
What's a locus? Is it a geometry term?
igloo myrtilles fourmis
Offline
#6 2007-09-18 00:41:10
- landof+
- Member
- Registered: 2007-03-24
- Posts: 131
Re: Geometry problem
That may be of some use.
I shall be on leave until I say so...
Offline
#7 2010-04-05 13:18:24
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Geometry problem
Bumping this because after two and a half years nobody appears to have a solution yet.
Offline
#8 2010-11-21 04:51:33
- 123ronnie321
- Member
- Registered: 2010-09-28
- Posts: 128
Re: Geometry problem
I am using your figure to solve this.
let the midpoint of PR be M
Let OQ = t < 2a
Let PQ = k.

PQ = P`Q` = k = 2P'M
PR = OQ = t = 2PM
PM^2 + P`M^2 = P`P^2 = a^2 ... Pythagoras theorem
therefore, k^2 + t^2 = (2a)^2. which is a circle if we make the following assumptions-
Let OQ act like x axis and and OR as Y axis.
Co ordinates of pt P are k,t.
Last edited by 123ronnie321 (2010-11-23 00:49:12)
Offline
#9 2010-11-21 10:47:59
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Geometry problem
Hi Jane,
I haven't been ignoring your problem since 2007. I've only been a member for 6 months or so.
So thanks for bringing back into attention.
See my two diagrams below. I set up what I thought was the right diagram and took the first screen shot. Then I moved Q left a bit and all that happened was moved the same amount (second half of shot).
Would you mind repeating the construction rules.
Mystified Bob ![]()
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#10 2010-11-22 01:06:07
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Geometry problem
Hi Jane Fairfax,
Ok, so I hadn't read the problem properly. Now I have.
Bob
Last edited by Bob (2010-11-22 01:07:53)
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#11 2010-11-22 23:28:09
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Geometry problem
Hi, Ronnie and Bob. ![]()
Offline
#12 2010-11-23 02:43:02
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,827
Re: Geometry problem
Hi Jane
I thought I'd already proved it in post 10.
Bob ![]()
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
Pages: 1