Geometry problem

JaneFairfax · 2007-08-19 23:16:21

Heres a geometry problem Ive just made up by myself.

Let O be a fixed point. Let Q be a variable point such that the length of OQ is less than or equal to 2a, where a is a fixed positive real number. Now let P and R be points satisfying the following conditions:

(i) OQPRO is a rectangle.
(ii) If PQ is shifted parallel to itself to P′Q′ such that P′Q′ and PR mutually bisect each other, then PP′RQ′P is a rhombus with sides of length a.

Prove that the locus of P is a circle of radius 2a.

Im sure it works. Still, if you find any problem with my problem, do let me know.

Last edited by JaneFairfax (2007-08-19 23:20:35)

John E. Franklin · 2007-08-21 13:05:32

Here are six red points.
Is that what you mean?
I only used up 279 bytes
on that small pic!!
The lower-center red dot
is Q prime, unmarked as such.

JaneFairfax · 2007-08-21 23:42:40

Thats right. I should have provided a diagram anyway, so here it is.

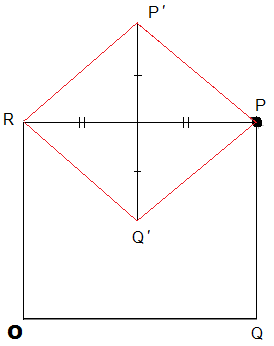
|P′Q′| = |PQ|
|PP′| = |P′R| = |RQ′| = |Q′P| = a
|OQ| ≤ 2a

Note that P can be below OQ as well, and that Q can also be to the left of O. Indeed, Q can be anywhere within a distance of 2a of O but for the purpose of analysis, we can assume WLOG that OQ is horizontal.

Last edited by JaneFairfax (2007-08-21 23:52:07)

JaneFairfax · 2007-08-23 23:55:49

John E. Franklin · 2007-08-27 08:59:48

What's a locus? Is it a geometry term?

landof+ · 2007-09-18 00:41:10

Definition of a locus

That may be of some use.

JaneFairfax · 2010-04-05 13:18:24

Bumping this because after two and a half years nobody appears to have a solution yet.

123ronnie321 · 2010-11-21 04:51:33

I am using your figure to solve this.

let the midpoint of PR be M
Let OQ = t < 2a
Let PQ = k.

PQ = P`Q` = k = 2P'M
PR = OQ = t = 2PM
PM^2 + P`M^2 = P`P^2 = a^2 ... Pythagoras theorem

therefore, k^2 + t^2 = (2a)^2. which is a circle if we make the following assumptions-
Let OQ act like x axis and and OR as Y axis.
Co ordinates of pt P are k,t.

Last edited by 123ronnie321 (2010-11-23 00:49:12)

Bob · 2010-11-21 10:47:59

Hi Jane,

I haven't been ignoring your problem since 2007. I've only been a member for 6 months or so.

So thanks for bringing back into attention.

See my two diagrams below. I set up what I thought was the right diagram and took the first screen shot. Then I moved Q left a bit and all that happened was moved the same amount (second half of shot).

Would you mind repeating the construction rules.

Mystified Bob

Bob · 2010-11-22 01:06:07

Hi Jane Fairfax,

Ok, so I hadn't read the problem properly. Now I have.

Bob

Last edited by Bob (2010-11-22 01:07:53)

JaneFairfax · 2010-11-22 23:28:09

Hi, Ronnie and Bob.

Bob · 2010-11-23 02:43:02

Hi Jane

I thought I'd already proved it in post 10.

Bob

Math Is Fun Forum

#1 2007-08-19 23:16:21

Geometry problem

#2 2007-08-21 13:05:32

Re: Geometry problem

#3 2007-08-21 23:42:40

Re: Geometry problem

#4 2007-08-23 23:55:49

Re: Geometry problem

#5 2007-08-27 08:59:48

Re: Geometry problem

#6 2007-09-18 00:41:10

Re: Geometry problem

#7 2010-04-05 13:18:24

Re: Geometry problem

#8 2010-11-21 04:51:33

Re: Geometry problem

#9 2010-11-21 10:47:59

Re: Geometry problem

#10 2010-11-22 01:06:07

Re: Geometry problem

#11 2010-11-22 23:28:09

Re: Geometry problem

#12 2010-11-23 02:43:02

Re: Geometry problem

Board footer