Math Is Fun Forum

You are right.
I did it using am gm inequality. Thanks for your time.

The longest side will be the hypotenuse.
Use the Pythagoras theorem to find the other side.....

This link will help you understand the basics of a triangle.
http://www.mathsisfun.com/triangle.html

I am using your figure to solve this.

let the midpoint of PR be M
Let OQ = t < 2a
Let PQ = k.

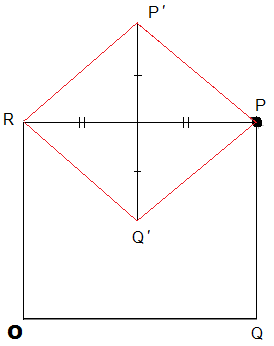
PQ = P`Q` = k = 2P'M
PR = OQ = t = 2PM
PM^2 + P`M^2 = P`P^2 = a^2        ...  Pythagoras theorem

therefore, k^2 + t^2 = (2a)^2. which is a circle if we make the following assumptions-
Let OQ act like x axis  and and OR as Y axis.
Co ordinates of pt P are k,t.

Ok,

bob and sameer,

to be honest i am not fully satisfied with either of your answers although they are correct. I think i should be more clear with what i am asking.

Can you say which one is obtuse angle bisector and which one acute just by putting some conditions on a,b,c,p,q,r. Like a computer programme.

If numerical values are given i am able to solve. This is what once our teacher had asked us.

thanks bob

yes, graphical method is the best.

All we hv to do is to prove that 9k^2 - 1 is divisible by 8.
=(3k+1)(3k-1) this reduces down to your other question -- product of 2 consecutive even nos is div by 8.......

(e^2x)/2 - (e^-2x)/2