Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: Help Me ! » how to know the number is prime or not buy using % ( mod ) » 2016-12-02 20:42:40
You're right that we can do a gcd of a primorial, which is a way to do quite a bit of trial division in one "operation". For large inputs, it's actually quite effective in GMP. In that case I wasn't doing full trial division, just speeding up the "is the input divisible by a prime under 40,000" for instance.
Once of the primary advantages of this is that the primorial can be made once and re-used. This means it's a little trickier for small inputs since the included primes can exceed the input, but we could just use a different method for those.
#2 Re: Help Me ! » how to know the number is prime or not buy using % ( mod ) » 2016-12-02 04:42:33
If a number n is not prime, it must be divisible by some prime <= sqrt(n). So we can check divisibility by all primes up to and including floor(sqrt(n)). The mod operator returns the remainder of n % p after division, so if it returns 0, the number is evenly divisible by p.
E.g. is 57 prime? sqrt(57) is ~7.55 so we need to check all primes through 7. So check 2,3,5,7.
57 % 2 = 1. Continue.
57 % 3 = 0. Found a factor. The number is composite.
Random thoughts:
- remember to include sqrt(n) so we catch perfect squares.
- you can use a test p*p <= n instead of p <= sqrt(n). They each have gotchas in computer implementation: p*p can overflow in most languages, sqrt(n) is not exact in most languages, sqrt(n) is computationally expensive in most languages. The fastest method is to make a variable to store floor(sqrt(n)) before the loop, and make sure you use a good integer square root method. Most of this is moot if you're testing small numbers rather than near the 64-bit boundary.
- ideally we test just the primes, but you can compromise by testing 2 then odds, or 2,3,5 then a +2,+4 wheel (aka a mod-6 wheel), or a mod-30 wheel, etc.
- You can't use a single mod as a deterministic test. You could store lots of primes and do a lookup, which gives an O(1) algorithm making certain assumptions about hashes or O(log n) making other assumptions or using a binary search through a linear table. This doesn't work once the input is larger than your table, and it's terribly memory inefficient. I have seen it done for tiny values (e.g. to 256 or to ~30,000) just because the primes were there. I'm not convinced it is better even if the table exists.
This method is actually one of the fastest for tiny numbers, under a million or so. After that, other methods such as deterministic Miller-Rabin or BPSW are faster. Note that properly implemented for 64-bit inputs, they are *not* probabilistic, but completely correct. For numbers of 20+ digits, the trial division method above is really not practical. We can start using probabilistic and fast methods (e.g. BPSW, which has no known counterexamples), or proof methods.
I'm not sure why AKS got mentioned. If you understand AKS, then trial division should be a trivial concept. AKS is probably not something you want to actually use, as it's quite slow compared to other proof methods. Albeit it is fun to program if you like number theory.
#3 Re: This is Cool » My New Twin Prime Numbers » 2015-07-02 19:04:10
By the way, here is what I used. Just brute force.
perl -Mntheory=:all -MMath::GMPz -E 'for my $pt (1..11) { for my $n (1 .. 50000) { my($sign,$s)=(1,0); forprimes { $s += $sign* Math::GMPz->new($_)**$pt; $sign=-$sign } nth_prime($n); if ($n < $s && is_provable_prime($s-$n) && is_provable_prime($s+$n)) { say "$pt: $s +/- $n"; last; } } }'Takes about 1.5 minutes. Generating the proofs vs. plain BPSW makes no noticeable timing difference.
1: 8 +/- 5
2: 20 +/- 3
3: 106 +/- 3
4: 560 +/- 3
5: 59779076418421204640 +/- 1281
6: 4255809704937643329920 +/- 609
7: 63835705531104194020747282 +/- 711
8: 5199099913899300539585745185120 +/- 957
9: 86486076326025141392980473635379192344452 +/- 4035
10: 1287183127776263297776662121192361760476608760 +/- 3723
11: 101678827728094895209692286827415375382 +/- 435I imagine this could be translated into Pari/GP with little effort, and its isprime is APR-CL with modern versions. Mathematica would probably not translate directly but should be easy enough. ProvablePrimeQ according to documentation uses various methods including ECPP, but I have no idea how fast it is.
#4 Re: This is Cool » My New Twin Prime Numbers » 2015-06-30 01:48:14
I didn't before (just using something similar to Mathematica's PrimeQ), but these numbers are small so I changed to is_provable_prime. They're provable primes (if they weren't we'd have found something that was a BPSW + extra M-R tests counterexample, which would be astonishing).
#5 Re: This is Cool » My New Twin Prime Numbers » 2015-06-28 10:15:51
Oh, I see. You're restricting n to both the number of terms and the +/- unit.
I believe for Pt=5, n=1281; Pt=6, n=609; Pt=7, n=711; Pt=8, n=957; Pt=9, n=4035. Double check them.
#6 Re: This is Cool » My New Twin Prime Numbers » 2015-06-27 16:20:43
Isn't that a solution for Pt=5? Similarly n=3 Pt=6 => +/-9, n=3 Pt=7 => +/- 63
#7 Re: This is Cool » Max Number of Consecutive Primes » 2014-12-31 17:23:38
Thanks danaj for the input. Can you list the 10 consecutive primes.
It's in post 15: p=247752179
247752179: 5286145759 5286145811 5286145829 5286145831 5286145841 5286145873 5286145951 5286145981 5286145999 5286146029You can do this with Mathematica like:
Table[Prime[247752179+i-1],{i,10}]or Perl/ntheory as:
perl -Mntheory=:all -E 'say nth_prime(247752179+$_) for 0..9;'or Pari/GP (slow) as:
for(i=0,9,print(prime(247752179+i)))or the faster but still much slower than the others Pari/GP:
s=prime(247752179); for(i=0,9,print(s);s=nextprime(s+1))#8 Re: This is Cool » Max Number of Consecutive Primes » 2014-12-30 19:08:33
PrimeQ uses, from the best documentation I know of, BPSW + a base 3 strong probable prime test. BPSW is deterministic for 64-bit numbers like we're using, much less adding another M-R test. There should be no reason to use ProvablePrimeQ here. Or another way of looking at it: use PrimeQ, then for the few found examples, use ProvablePrimeQ -- if something comes up false then you have a great example of Mathematica doing something wrong.
Pari/GP has isprime() (like I put in the example) which is deterministic (BPSW then APR-CL if large), or ispseudoprime for just BPSW. They're identical for 64-bit inputs. Perl/ntheory has is_provable_prime() to do a proof, but similarly it is identical to is_prime or is_prob_prime for 64-bit inputs.
"So far, 8 is the largest." There is an example of 10, but I did not find anything higher than that.
#9 Re: This is Cool » Max Number of Consecutive Primes » 2014-12-30 13:42:05
This takes the 'p' values and computes the 8 's' values corresponding to prime[p+0], prime[p+1], ..., prime[p+7]. Of course the 's' values are prime and sequential, but we can also check that for each one, 34+3*s is also prime. I will note that the 34+3s results are not sequential primes -- it's hard to tell if this is expected in the original post, but your posted results don't have them sequential.
These are just the values for 8. The runs of 9 and 10 would also be runs of 8.
I'm surprised Mathematica isn't faster. It uses a BPSW+1MR for large inputs, and may drop the extra MR for these small numbers where BPSW is deterministic. That would match Pari and Perl/ntheory. The forprime() call does help since we can easily loop through the primes.
for my $s (qw/13155307 23373712 28619826 206480632 430788664 451840108 723650223 778689176 922591383 943068103 1005001898 1083424548 1406260752 1528839396 1653992654 1884407047 2112863733 2420339382 2444147088 2467436354 2559176982 3141752981 3239363657 3314161732 3346438597 3510021953/) { say "$p: ", join(" ",map { nth_prime($p+$_) } 0..7); }'13155307: 239878543 239878571 239878579 239878603 239878621 239878649 239878663 239878673
23373712: 440460583 440460589 440460593 440460619 440460623 440460659 440460673 440460703
28619826: 545465579 545465593 545465633 545465659 545465731 545465743 545465749 545465759
206480632: 4365959711 4365959713 4365959753 4365959779 4365959789 4365959809 4365959879 4365959909
430788664: 9442018519 9442018559 9442018583 9442018589 9442018601 9442018609 9442018613 9442018643
451840108: 9926055071 9926055079 9926055131 9926055133 9926055143 9926055163 9926055169 9926055173
723650223: 16255022843 16255022851 16255022863 16255022869 16255022939 16255022941 16255022969 16255023019
778689176: 17551241549 17551241551 17551241563 17551241579 17551241581 17551241593 17551241611 17551241639
922591383: 20958804241 20958804271 20958804283 20958804323 20958804341 20958804343 20958804371 20958804413
943068103: 21445686761 21445686781 21445686791 21445686793 21445686811 21445686839 21445686851 21445686901
1005001898: 22921075381 22921075409 22921075421 22921075423 22921075433 22921075451 22921075493 22921075501
1083424548: 24795040741 24795040759 24795040801 24795040903 24795040931 24795040943 24795040951 24795040969
1406260752: 32567701541 32567701561 32567701571 32567701609 32567701631 32567701643 32567701693 32567701709
1528839396: 35540355871 35540355881 35540355889 35540355901 35540355911 35540355923 35540355953 35540355959
1653992654: 38585987383 38585987399 38585987413 38585987441 38585987509 38585987519 38585987549 38585987591
1884407047: 44218726703 44218726723 44218726763 44218726793 44218726813 44218726829 44218726859 44218726913
2112863733: 49832772751 49832772763 49832772791 49832772793 49832772811 49832772851 49832772943 49832772961
2420339382: 57428667449 57428667473 57428667509 57428667529 57428667613 57428667671 57428667701 57428667799
2444147088: 58018595399 58018595419 58018595431 58018595443 58018595461 58018595483 58018595501 58018595519
2467436354: 58595995259 58595995273 58595995279 58595995319 58595995331 58595995349 58595995363 58595995439
2559176982: 60872272801 60872272819 60872272829 60872272859 60872272889 60872272913 60872272931 60872272933
3141752981: 75403452713 75403452721 75403452749 75403452781 75403452799 75403452811 75403452833 75403452881
3239363657: 77849739503 77849739521 77849739529 77849739589 77849739619 77849739659 77849739673 77849739719
3314161732: 79726451263 79726451293 79726451303 79726451353 79726451393 79726451443 79726451459 79726451503
3346438597: 80536791493 80536791509 80536791521 80536791553 80536791583 80536791611 80536791623 80536791659
3510021953: 84648776909 84648776911 84648776921 84648776939 84648776941 84648776963 84648776999 84648777019#10 Re: This is Cool » Max Number of Consecutive Primes » 2014-12-30 08:57:58
I can send you my perl script if you'd like. It takes 15s to find three 8-consecutives for s < 1e9. Searching to s < 1e10 takes about 2.5 minutes:
7 1718020 2492520 2671928 3036055 3562655 3594150 10654019 15191513 15626334 21063558 21752023 22152282 25059807 27161939 29545494 32921098 37188348 44503753 46206335 51087603 51960322 54481455 57923734 63665188 65256256 65443263 68573108 69790405 69888940 72402885 89135244 91447387 96231989 96907585 98870702 104486689 106724222 108468644 110963047 123035310 126428987 133783990 140775016 153601104 156826152 158202292 163519132 166930965 179742892 184518605 185994353 188583675 192392346 203631792 205873490 212190182 218841344 232714800 256292473 261209858 276867166 283985400 289567855 304492904 305351642 319820383 322860650 323803818 335518221 344398882 361505496 366930942 385324698 395261357 399795913 415012199 420673304 422144423 426839424 435086906 441592465 453986477
8 13155307 23373712 28619826 206480632 430788664 451840108
9 62888993
10 247752179Searching to s < 1e11 (100,000,000,000) took 21 minutes:
7 1718020 2492520 2671928 3036055 3562655 3594150 10654019 15191513 15626334 21063558 21752023 22152282 25059807 27161939 29545494 32921098 37188348 44503753 46206335 51087603 51960322 54481455 57923734 63665188 65256256 65443263 68573108 69790405 69888940 72402885 89135244 91447387 96231989 96907585 98870702 104486689 106724222 108468644 110963047 123035310 126428987 133783990 140775016 153601104 156826152 158202292 163519132 166930965 179742892 184518605 185994353 188583675 192392346 203631792 205873490 212190182 218841344 232714800 256292473 261209858 276867166 283985400 289567855 304492904 305351642 319820383 322860650 323803818 335518221 344398882 361505496 366930942 385324698 395261357 399795913 415012199 420673304 422144423 426839424 435086906 441592465 453986477 466621403 466955611 470479122 475281381 478099131 486581146 488574100 492974241 495709419 503242169 514290308 524353559 526210953 547238431 555377530 560568673 563819394 564050336 565117578 567697430 574333477 581719259 604397264 605285517 609953548 611506702 619023097 627335360 644365306 664376162 665037413 686007851 718559335 725439993 735943665 743431923 746057515 748880752 750680263 794532893 797034046 807908141 817185739 830061428 838793990 844170390 847996148 863088773 868761819 872583472 875894406 880427154 885068607 885730110 886707614 897000052 922799091 930122687 949561295 953536846 965574106 970670184 971616015 984136807 999904292 1032348520 1032626596 1038415609 1042590507 1063551577 1071083510 1084818946 1092401906 1092937465 1095569057 1097103079 1121692213 1127021960 1141442850 1142159307 1167453552 1179332930 1198709921 1207536623 1225783001 1226020529 1226973918 1230881242 1255337127 1266567073 1269833145 1288913145 1301900559 1315347414 1330558720 1335151552 1336167535 1336470638 1357529972 1366303467 1367532201 1394632344 1415994612 1425615667 1468126216 1479052712 1484197484 1484664232 1499162590 1510892825 1525540560 1538768858 1541431708 1547113639 1561569771 1573285197 1575338467 1608245600 1620892699 1636594726 1639912926 1642785097 1649448543 1658387196 1659492894 1669878049 1673030859 1680288649 1689009936 1705139805 1707877965 1720548461 1725560049 1727975655 1740450178 1757696409 1767977017 1774252457 1783722479 1833272684 1835641302 1864180009 1875220655 1894374764 1914950297 1925191608 1930188541 1944046812 1947734807 1950943878 1961537003 1968415550 1978950200 1983147463 1992503523 2003383667 2011759321 2036328796 2074864705 2083105576 2097268421 2120562842 2131335524 2173046960 2174549806 2197537096 2206149990 2239254808 2243414356 2349463495 2368648878 2388262838 2397241591 2398126033 2403896576 2417795626 2421180508 2427214723 2433644912 2460192669 2464829434 2466386056 2470597216 2473662702 2477156833 2481924935 2486632950 2535173281 2562687057 2577546536 2594427982 2602427582 2615924025 2627636732 2648467667 2681906133 2708967552 2721761110 2741304277 2746549938 2750335395 2753208097 2763210973 2766258139 2777676867 2787956664 2817979773 2820157908 2837602399 2869185904 2878113684 2882066301 2884645265 2912256157 2935732944 2939577836 2946296457 2955639898 2961631157 2989076982 2996581210 3004860881 3019444513 3024664264 3026879459 3092518506 3094303338 3099197655 3127207507 3128262874 3140049442 3157014173 3175544783 3193904988 3194803790 3202819376 3217890148 3225417795 3229520764 3232636927 3244256924 3258840570 3277320913 3278576127 3285898935 3296994608 3312205351 3332431095 3342688030 3367721960 3380264281 3384164887 3396537088 3402359710 3403327218 3406882404 3419374349 3453540047 3473030524 3478573403 3487003920 3489342936 3541544528 3553821171 3563989241 3570263926 3579929644 3600057302 3606082748 3608868228 3612932294 3628577024 3631111020 3639429262 3648181186 3664377198 3676997253 3694484527 3733723540 3750029130 3770734294 3792743589 3807294468 3809322646 3818970943 3826632839 3852382997 3864241176 3937518769 3964472367 3968680328 3978909813 3980535308 3989589875 4032468634 4043649533 4045499779 4059220413 4091714016 4092344452 4097893987 4103216975 4104895899
8 13155307 23373712 28619826 206480632 430788664 451840108 723650223 778689176 922591383 943068103 1005001898 1083424548 1406260752 1528839396 1653992654 1884407047 2112863733 2420339382 2444147088 2467436354 2559176982 3141752981 3239363657 3314161732 3346438597 3510021953
9 62888993 2337819127 2805299994 3543590679 3649181083
10 247752179Here is a Pari/GP version. It runs slower than Perl's ntheory for this, but it's not too bad (it needs Pari 2.8):
s=0;sr=0;cr=0;forprime(p=1,1e9,s++;if(isprime(34+3*p),cr++,if(cr-sr>=7,print(cr-sr," ",sr));cr=s+1;sr=s+1))#11 Re: This is Cool » Max Number of Consecutive Primes » 2014-12-27 13:17:52
length and p, where s = nth_prime(p) and 34+3s is prime; length the first run of consecutive p values
6 1373
7 1718020
8 13155307
9 62888993
10 247752179
For 82+5s:
6 131582
7 245075654
8 7358058514
Simple brute force walking primes looking at primality of 34+3s or 82+5s for s < 1e12. No easy answers past these for this search method.
#12 Re: Euler Avenue » What had you learned today that you found interesting? » 2014-12-03 01:02:42
http://docserv.uni-duesseldorf.de/servlets/DocumentServlet?id=26247
and
http://arxiv.org/abs/1409.1780
Improvements to the Dusart (2010) bounds on prime count and nth prime. I also started playing around with nth prime limits via binary search on prime count bounds, which tentatively looks like a nice improvement (indicating that the prime count bound formulas are tighter than the nth prime bound formulas).
Also, someone finished computation of Pi(10^26) via combinatorial methods.
#13 Re: Jokes » Experimental Mathematics Troll » 2014-10-23 19:16:27
I did it this way, which is longer but lets one see all the results. Perl:
use ntheory qw/:all/;
my @I = qw(A a B b C c); # lower case = child, upper case = guardian
forperm {
my $s = "@I[@_]"; # the permuted string
say $s unless $s =~ /a.*A|b.*B|c.*C/; # print unless child precedes its guardian
} 6;which prints out the 90 cases as: "A a B b C c" , "A a B C b c", "A a B C c b", etc. There are lots of ways to structure the restriction (e.g. a hash of positions, then do position comparisons).
#14 Re: This is Cool » My New Twin Prime Numbers » 2014-10-20 17:10:23
Having 1024 nodes with 4 2880-core GPUs each doesn't solve anything if there isn't an application to run on it. Do you have something in mind?
Trial division would be trivial to parallelize, but is basically worthless. I see a paper by Asaduzzaman et al. from 2014 saying they have sped it up on GPUs, but (1) that's not hard, and (2) their comparison CPU code is 100x slower than the single-core CPU code I use, making their 90x speedup claim dubious. One thing that bothered me at GTC was the uncertainty around speedup numbers -- it's easy to get 100x speedup if you write cruddy CPU code in a weekend and then compare to GPU code you had four people working 6 months on.
AKS should be pretty easy to run in parallel (each of the s tests are independent), and the code that takes 99% of the time is pretty simple. You need to do lots and lots and lots of s += (a * b) % n type operations. Some problems:
[list=*]
[*]The growth rate difference means ECPP or APRCL on a single host will beat the hundreds of thousands of GPU cores running AKS. If the serial algorithm takes many trillions of years, how many cores will we need to make it run in an hour? Do you have that many GPUs?[/*]
[*]There is no certificate, so realistically your saying you ran this is no better than just saying you used well-known software to run BPSW + a Frobenius test + some number of random-base M-R tests. Less for me because I've seen too many broken AKS implementations. It doesn't matter how fast it is if it isn't correct.[/*]
[/list]
There may be other tricks for AKS that can help, but you have to make major changes to it to get it to the same growth rate as APR-CL or ECPP. There are definitely some research opportunities here.
The BLS75 methods involve factoring, so won't scale to usefully large numbers.
I don't know how well APRCL would parallelize. I think there was a thesis about the subject, but it didn't give much detail.
ECPP certainly could benefit if you could write it. If you do, please make it open source and publicize it. That would be a major accomplishment of use to many people. There are quite a few places where things could run in parallel (the fanout is extremely large if you run speculatively).
#15 Re: This is Cool » My New Twin Prime Numbers » 2014-10-20 03:28:08
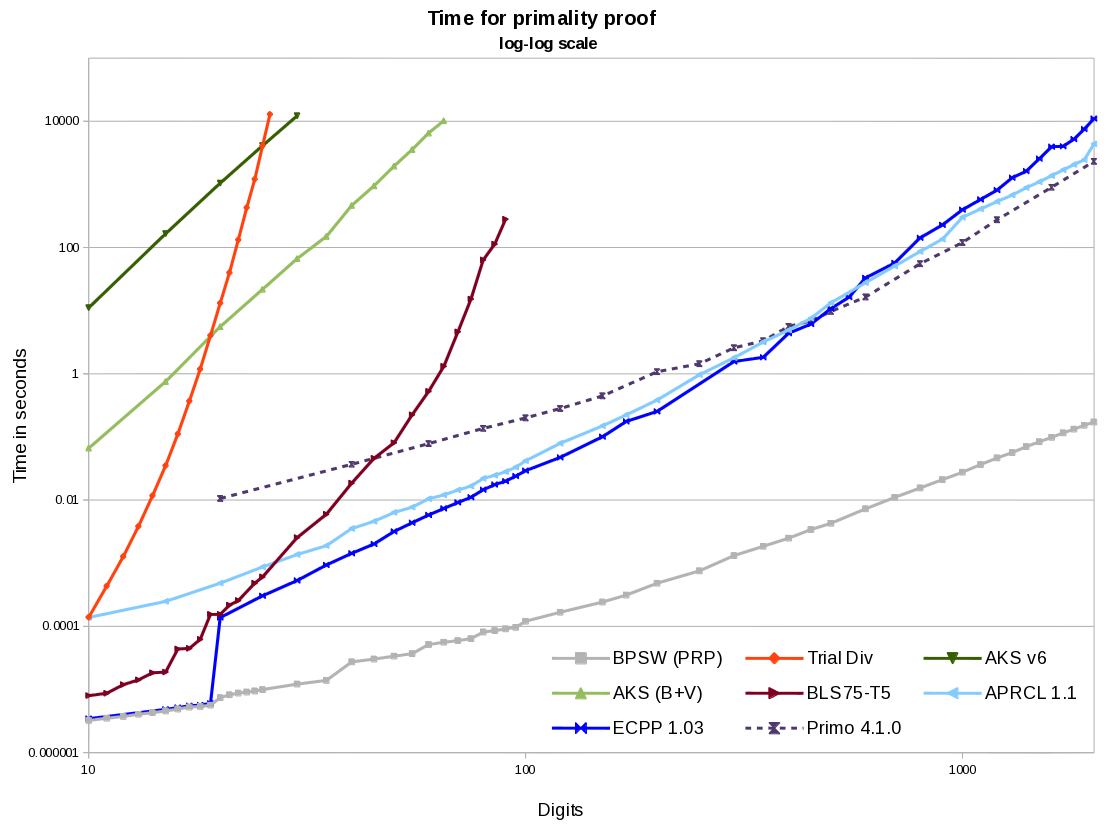
Here is an example graph showing some times for primality proving. Single threaded on a 4.3GHz machine (more details available if you'd like). I have not seen a faster AKS implementation than the B+V version here, but they could be out there. Pari/GP's APR-CL (the isprime command) runs a bit slower than WraithX's APRCL 1.1. I have no idea how fast Mathematica is (timings from this thread make me think its BPSW is quite a bit slower than the graph here, but that is independent from its proof times). Primo is the most common program used for proving large general primes.
100 digit primes can be proved extremely fast (a few milliseconds). 1000 digits will take ~2-8 minutes. For ECPP and APR-CL the time increases at about the 4th power of the number of digits (for AKS it's the 6th power). By 20k digits, expect 3 months using all cores of a 4- or 6-core machine.
I'm not sure about the various DR-restricted numbers, but the first set of unrestricted (post 109) are fairly small. E.g. p=29 => n=932651 is 213 digits, p=31 => n=2547137 is 242 digits. They grow of course, as p=59 => n=4183583 is 469 digits.
#16 Re: Help Me ! » Permutation Problems » 2014-09-06 21:05:21
Since I just added a permutation iterator to my module yesterday, this is a convenient time to try it. Using the hash to not count duplicates.
my %h;
my @m = split "", "mathematics";
forperm {
my $s = join "", @m[@_];
undef $h{$s} if $s =~ /a.*e.*a.*i/;
# alternate: undef $h{$s} if $s =~ tr/aeiou//cdr eq "aeai"
} scalar(@m);
say scalar keys %h;Result match's Bobbym's analytic answer. Thanks for the fun!
#17 Re: This is Cool » Find all the prime numbers in a given range.... » 2014-08-28 20:07:16
What is the advantage of this over the well known Sieve of Eratosthenes?
I think you meant to say "up to a limit" (e.g. find all primes up to 29) instead of "in a given range" (e.g. find all primes in the range 5,208,079 and 6,206,197).
#18 Re: This is Cool » Tests of Divisibility- Simple tricks » 2014-08-07 16:37:12
Many more, alternate methods, and examples: Wikipedia: Divisibility rule
#19 Re: Coder's Corner » Just another perl hacker » 2014-07-18 03:58:03
(p.s. the talk at YAPC was by me, so we have a little Perl representation)
I didn't know I was supposed to ask a question... Will we have a proof of the Riemann Hypothesis by 2059?
#20 Re: Coder's Corner » Just another perl hacker » 2014-07-17 00:57:23
Indeed there are.
There was even a "Perl and Scientific Programming" panel at YAPC this year, and someone gave a lightning talk about a Perl number theory package.
#21 Re: Coder's Corner » AKS performance » 2014-06-07 08:51:56
Sorry for not including the link. It was here as well: http://www.mathisfunforum.com/viewtopic … 75#p273775.
Re implementation, Darn -- I was hoping to find something new! Thanks for looking.
#22 Coder's Corner » AKS performance » 2014-06-07 07:06:15
- danaj
- Replies: 3
A year ago, bobbym wrote:
They are right about AKS, it takes about an hour to prove the primality of a 1000 digit number on an old desktop.
Can you point me to the software you're using? This is much faster than any AKS implementation I am aware of. It's millions of times faster than stated performance numbers in papers about AKS implementations, e.g.
- Crandall and Papadopoulos (2003) "A 30-decimal-digit prime this took, [...], about a day to be resolved."
- Rotella (2005), "An Efficient Implementation of [AKS]" takes a minute for 4 digit numbers, and ends with "[...]the AKS algorithm, while it is elegant and relatively simple, should be viewed as an algorithmic curiosity rather than an algorithm to be used for actual primality proving."
- Salembier and Southerington (2006) show a time of 30 minutes for a 15 digit number.
- Brent (2010) estimates 840 years for a 308 digit prime using a version with some improvements.
My code/machine is running about 200 times faster than Brent's numbers, and I come up with en estimate of about 4200 years for a 1000 digit number. APR-CL and ECPP are about 2-5 minutes (single threaded) for 1k digits on the same computer.
#23 Re: Help Me ! » Intersections of sets of primes » 2014-03-18 17:24:01
There are plenty of other not-uncommonly-discussed sets as well, e.g. Safe, Sophie Germain, Lucas, Fibonacci, Lucky, Palindromic, Pillai, Good, Cuban (y+1, y+2), Primorial (+1, -1), Euclid, Circular, Panaitopol. (Re digressing about Euclid and Primorial, one wants to distinguish between P#+/-1 and Pn#+/-1 -- that is primes up to P or the Pn-th prime). I'm sure one could come up with another hundred sets. Surveying OEIS would bring up lots of them, for example.
For intersections, I found a useful practical method to be listing the allowable subsets of n mod 210 for each type. Some don't have a pattern, but many do (e.g. cuban1, cuban2, twin, triplet, quadruplet, cousin, sexy, safe, sophie, panaitopol to name some). Not only does this help for single cases, but one can then do the intersection of the two (or 3 or more) types. Sometimes this yields a null set once past tiny numbers (e.g. quadruplet cuban primes, or safe quadruplets other than 5 and 11).
This doesn't really help answer the original questions however. For my reading of the first question, certainly we can find examples where sets intersect, e.g. twin sexy primes, or titanic cousin primes (e.g. 10^1000 + 744843).
I believe the answer to your second question is no in general. In some of the cases, the number of intersections from A to B between two sets will not necessarily follow the same trend as between A to B+delta. In other cases (what I believe most people are discussing) both sets will be infinite, though maybe it would be possible to prove that the number of elements of set P in an interval is always greater than the number of elements of set Q in the same interval, or compare asymptotic densities, or something along those lines (e.g. the density of titanic primes in an interval starting after 10^1000 is going to be at least as dense as any of the restricted sets in the same interval).
#24 Re: This is Cool » Large Prime » 2014-03-14 17:56:17
I'm not sure if I should post, (1) it is somewhat necro-posting, (2) there seems to be another conversation going on about DH, and (3) I type way too much. But regarding generating large primes, this is a good paper about generating n-bit random primes: "Close to Uniform Prime Number Generation With Fewer Random Bits" by Fouque and Tibouchi available at eprint.iacr.org/2011/481. For crypto, you may want to also look at FIPS 186-4.
PRIMEINC: generate a random number in the range, run next_prime on it. Simple and fast, but bad distribution.
Trivial: Aka Monte Carlo method as in post 3. Perfectly uniform, but uses excessive randomness and is very slow for large sizes. A comment about the post 3 code: for sizes over 2 bits, you'd want to take n-2 random bits and then set bits n-1 and 0 -- there is no need to waste time and entropy testing even numbers. A well written test will return almost instantly, but you wasted time getting all those bits -- if you're on an isolated headless server using /dev/random you may wait hours to get the next set.
Modified: Methods like Fouque and Tibouchi A1 or A2; Joye-Paillier, etc. I use a somewhat similar method for odd ranges (e.g. for ranges not a power of 2). These sacrifice some uniformity for big increases in speed and less entropy consumption. (the entropy consumption may or may not matter to you, but sometimes it is important).
Provable primes, typically Shawe-Taylor or Maurer's FastPrime. Common for crypto use. You can find Shawe-Taylor in FIPS 186-4; Maurer's algorithm in his publicly available paper, Menezes's book, or various open source implementations. These work by generating a small random prime using the trivial method, then generating a larger one by iterating with additional random input until proven with either Pocklington or its improved version from BLS theorem 3. Then recurse to make successively larger primes. They only generate a subset of the primes in the range (10% for Maurer's FastPrime, substantially less for Shawe-Taylor) but that typically doesn't matter.
openssl or other software. Good and bad. OpenSSL likely doesn't make some mistakes you may make. But you have to make sure your platform has a recent version, your program actually calls the right executable, you send it the right arguments, you interpret the output and exceptions properly, you're ok with its decisions on randomness sources, you're OK with it not meeting FIPS 186-4 standards for primality testing, and know it is slower for sizes > 1024 than what can be done with GMP meeting the standards.
There are lots of other considerations. E.g. where are you getting your randomness? Are you using a good enough primality test for your purpose? Do you need provable primes? Strong primes? Writing your own code is fun, but may have bugs -- do lots of testing.
Whether these are "quick" or not depends on the size, which method you choose, your implementations, and what you think quick means. For 1024-bit primes, my older machine using Perl code generates them in 0.06s each (F&T algorithm 1, ISAAC seeded from /dev/random, BPSW + 1 M-R probable primes). Add 0.006s for 3 additional random M-R plus a Frobenius test. Add not much more for enough extra M-R tests to make FIPS 186-4 happy. For smaller sizes sometimes running a primality proof on the n-bit prime is faster than a constructive method, but your mileage may vary. At 1024 bits, my Maurer routine takes 0.65s, while Shawe-Taylor using FIPS 186-4 + SHA256 takes 0.24s. The generation code is in Perl so it could be faster, but the heavy work ends up being in C+GMP.
#25 Re: Help Me ! » Is it any pseudo pattern gives prime number in proper range? » 2014-03-07 18:57:26
In the example for "is 281 prime" you did:
1. find squre root of number near about it is 17
2 17*=Pn*=510510
3 Ip17 =number not divisible by 2,3,5,7,9,...17
then: prime= Ip17-Pn* where IP17 started at 510513, and Pn* was 510510.
For the example "111,111,111,111,111" (decimal), I get a square root of 10540925. Step 2 as well as the prime generation says to use Pn*=10530925#. That came out to 4,576,061 digits for me. The number in "No of Ipn sub series" is going to be similarly titanic. What is different about this example from the 281 example?
You have to either store these or calculate them, and either way I don't see how you can say "don't worry about time [...] to find them." Why not just precalculate the primes directly if we get to discount the time and/or space?