Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2013-04-19 20:28:37
- anna_gg
- Member
- Registered: 2012-01-10
- Posts: 232
Regular concave polygons
What is the regular concave polygon with the smallest number of sides?
All its sides must be equal and all its internal or external angles must be equal as well (i.e. all its internal angles must be either equal or negative, that is, either θ or -θ).
Offline
#2 2013-04-20 00:39:34
Re: Regular concave polygons
A concave quadrilateral.
You can show that a triangle is never concave using the angle sum property
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#3 2013-04-20 02:08:28
- anna_gg
- Member
- Registered: 2012-01-10
- Posts: 232
Re: Regular concave polygons
Can you design it?
Offline
#4 2013-04-20 02:36:31
- Mathegocart
- Member

- Registered: 2012-04-29
- Posts: 2,226
Re: Regular concave polygons
here 
The integral of hope is reality.
May bobbym have a wonderful time in the pearly gates of heaven.
He will be sorely missed.
Offline
#5 2013-04-20 02:44:44
Re: Regular concave polygons
I am sorry, I didnt notice 'Regular'.
I don't think any regular polygon can be concave
Do you want me to prove it?
Last edited by Agnishom (2013-04-20 04:24:13)
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#6 2013-04-20 03:51:57
- anna_gg
- Member
- Registered: 2012-01-10
- Posts: 232
Re: Regular concave polygons
I said concave, not convex. By "regular concave", I mean a concave polygon of which all the sides are equal and all its internal or external angles equal (that is, all the angles must be either θ or 360-θ).
Offline
#7 2013-04-20 04:09:23
- Nehushtan
- Member

- Registered: 2013-03-09
- Posts: 957
Re: Regular concave polygons
What is the regular concave polygon with the smallest number of sides?
All its sides must be equal and all its internal or external angles must be equal as well (i.e. all its internal angles must be either equal or negative, that is, either θ or -θ).
I think its a concave dodecagon

Last edited by Nehushtan (2013-04-21 00:18:45)
240 books currently added on Goodreads
Offline
#8 2013-04-20 23:27:02
- anna_gg
- Member
- Registered: 2012-01-10
- Posts: 232
Re: Regular concave polygons
This was also my solution but it seems there is a polygon with fewer sides that meets the criteria.
Offline
#9 2013-04-20 23:40:14
- Mrwhy
- Member
- Registered: 2012-07-02
- Posts: 52
Re: Regular concave polygons
There are stars
5 pointed
6 pointed
7 pointed
I reckon the 5 pointed has 10 sides
Offline
#10 2013-04-20 23:52:23
- anna_gg
- Member
- Registered: 2012-01-10
- Posts: 232
Re: Regular concave polygons
Yet the stars cannot have all their internal angles equal to θ or to 360-θ...
Offline
#11 2013-04-21 00:34:10
Re: Regular concave polygons
What is the answer anyway?
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#12 2013-04-21 02:57:10
- Nehushtan
- Member

- Registered: 2013-03-09
- Posts: 957
Re: Regular concave polygons
This was also my solution but it seems there is a polygon with fewer sides that meets the criteria.
Why, of course! A concave decagon.
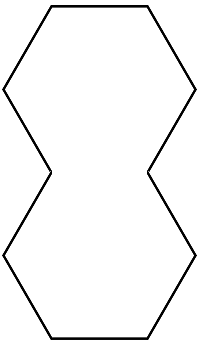
NB: I think Ive proved that a regular concave polygon (i.e. a polygon with equal sides and internal angles either θ or 360°−θ, at least one of which is reflex) must have at least 9 sides. If my proof is correct, it remains to check whether there exists any regular concave nonagon.
240 books currently added on Goodreads
Offline
#13 2013-04-21 04:21:38
- anna_gg
- Member
- Registered: 2012-01-10
- Posts: 232
Re: Regular concave polygons
Correct ![]()
![]()
Offline
Pages: 1