You are not logged in.
Pages: 1
#1 2012-09-22 20:41:46
- benice
- Full Member
Offline
Plot functions defined on rational numbers and irrational numbers
Hi All,
Suppose f1, f2, and g are arbitrary functions of real variables.
Let
f(x) =
f1(x) if x is rational,
f2(x) if x is irrational.
What software can be used to define f(x) such that we can plot y = f(g(x)) directly?
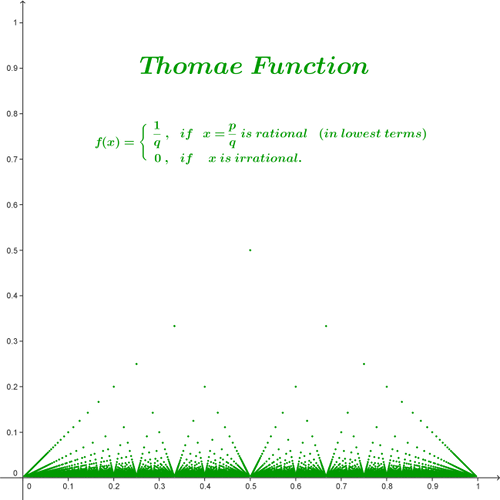
For example, consider the Thomae function:
f(x) =
1/q if x=p/q is rational, gcd(p,q)=1 and q>0,
0 if x is irrational.
How to define f as a function such that we can plot y = f(sin(x)) directly?
My Gallery of Math Art: benice equation
#2 2012-09-22 22:12:45
- bobbym
- Administrator
Offline
Re: Plot functions defined on rational numbers and irrational numbers
Hi benice;
Looks like it is going to be tricky using the Dirichlet-Thomae function.
Just generating that function is a chore. The best solution I think is showed by J.M. over at the stackexchange. He generates lots of rationals using a farey sequence and then just plots them. See below first picture, it looks like yours.
How did you generate your points, did you use a farey sequence too?
Do you have a rationalize command in the language or grapher you are using? If you do then there is a way, see the second picture that is f(sin(x)), I think.
In mathematics, you don't understand things. You just get used to them.
90% of mathematicians do not understand 90% of currently published mathematics.
I am willing to wager that over 75% of the new words that appeared were nothing more than spelling errors that caught on.
#3 2012-09-26 08:36:34
- benice
- Full Member
Offline
Re: Plot functions defined on rational numbers and irrational numbers
bobbym wrote:
How did you generate your points, did you use a farey sequence too?
Hi,
I used the GeoGebra command 'Sequence' to generate those points:
Sequence[Sequence[(p/q,GCD[p,q]/q),p,1,q-1],q,2,300] .
bobbym wrote:
Do you have a rationalize command in the language or grapher you are using? If you do then there is a way
I have downloaded Maxima 5.28 (which has a rationalize command), but I have no idea how to do that.
Yesterday, I constructed an approximate method which can plot the graph of y = f(sin(x)) directly.
( See this page for some examples. )
Thank you for your help bobbym!
My Gallery of Math Art: benice equation
#4 2012-09-26 09:44:40
- bobbym
- Administrator
Offline
Re: Plot functions defined on rational numbers and irrational numbers
I have downloaded Maxima 5.28 (which has a rationalize command), but I have no idea how to do that.
The trick is to generate rationals. That is what Rationalize does.
1) Make a function called fubar in your language.
fubar[n_]:=Rationalize[Sin[x]] ( In mathematica )
2) Generate a sequence from 1/5000 to 1 with a step size of 1 /5000 using on fubar for each number.
3) Take the denominator of each of these numbers in the sequence and invert it. In other words 1 / denominator. That is how I generated the composition, f(g(x)).
In mathematics, you don't understand things. You just get used to them.
90% of mathematicians do not understand 90% of currently published mathematics.
I am willing to wager that over 75% of the new words that appeared were nothing more than spelling errors that caught on.
Pages: 1