Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2005-12-29 11:06:37
- katy
- Member
- Registered: 2005-12-28
- Posts: 14
Inverse Functions!??
hi..I need help with these two questions from my Review Sheet...
1)What are two different ways one could determine if one function is the inverse of another?Give an example of each way.
2)Explain why the inverse of a quadratic function is not a function?What do we do to ensure that the inverse of a quadratic is a function?Give an example.
thanks in advance...
Offline
#2 2005-12-29 11:29:38
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: Inverse Functions!??
I way:
i think if we can proof that f[g[x]] = x
For example: f[x]=2x; g[x]=x/2
f[g[x]]=2(x/2)=x
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#3 2005-12-29 11:34:02
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: Inverse Functions!??
2) x^2 hasn't inverse function because there exist two solutions of
x^2=y
x1=sqr(y)
x2=-sqr(y)
So inverse function must have 2 different values at point y.
To reduce this we need to use only positive x in the first function.
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#4 2005-12-29 11:37:20
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: Inverse Functions!??
But we may say:
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#5 2005-12-29 11:43:25
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: Inverse Functions!??
Plots:
Last edited by krassi_holmz (2005-12-29 11:49:36)
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#6 2005-12-29 12:43:22
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Inverse Functions!??
Two ways you can prove it? The only way I know is this:
if g(x) is the inverse of f(x) then g(f(x)) = x I can't think of another way other then maybe doing it backwards: f(g(x)). Both will give you x if they are inverse functions.
I think I remember reading something about decomposing functions, I'll take a look.
Last edited by mikau (2005-12-29 12:43:51)
A logarithm is just a misspelled algorithm.
Offline
#7 2005-12-29 12:54:24
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Inverse Functions!??
Ah, I forgot. The graphs of an inverse function is the graph of the original function, reflected about the line y = x. So you could also draw a graph of the two functions and determine whether they appear to be relfections about the line y = x.
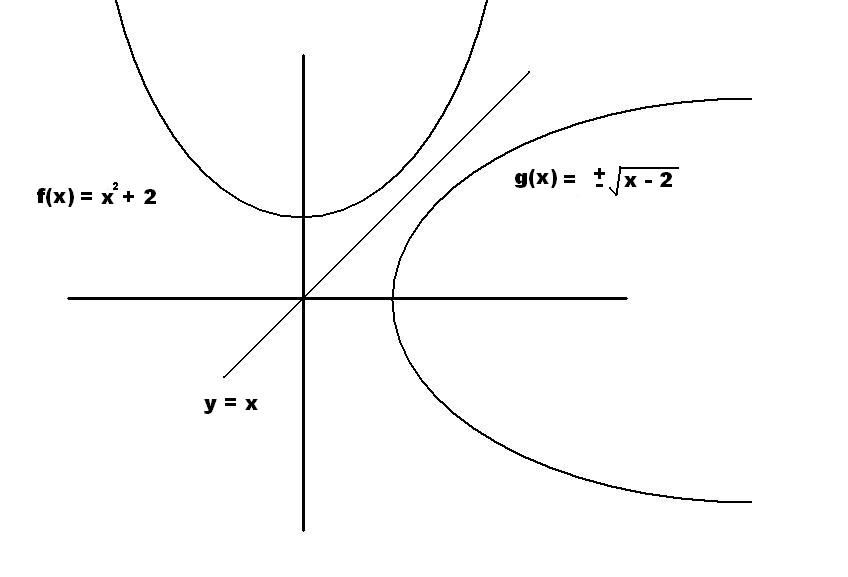
technically g(x) is not a function as a function only returns one value for a given input. It does not pass the vertical line test and does not qualify as a function. I just drew it that way to illustrate how the reflection works.
Last edited by mikau (2005-12-29 13:15:07)
A logarithm is just a misspelled algorithm.
Offline
Pages: 1