Math Is Fun Forum

Is such a sequence possible?

As bobbym pointed out, n must be a perfect square. n=1 is one possibility. For the others, it can be easily checked that all odd perfect squares greater than 1 and less than 1000 are have at most two distinct prime factors in their factorization. Thus the possibilities for n>1 are:

where p and q are distinct primes and a, b positive integers.

First case:

The number of positive divisors of n are

– i.e. there are

positive divisors. So the possibilites are

and

. (Not

; that would make n too large.)

Second case:

There are only two such

possible, namely

and

. The number of positive divisors for each number is 9, which does divide each number.

Therefore the answer to your question is: There are 5 odd numbers less than 1000 which are divisible by their number of positive divisors, namely 1, 9, 225, 441, and 625.

In what sense “more than”?

If an odds give you more returs when you win, we say the odds are longer; otherwise they are shorter. The longer the odds on a horse, the less probability it has of winning.

I think it’s better to avoid the terms “greater/more than” or “less than” to avoid confusion. Thus we say that the odds of 7/5 are longer than those of 1/2 (2/1 on).

1/2 means if you bet £1 and you win, you receive £1.50 (1/2 × £1 = £0.50 plus £1 stake).

1/2 is read as “2 to 1 on”.

For 2/3, £3 wins £2 plus £3 = £5. If you had staked the £3 on the 1/2 above however you would have got £1.5 + £3 = £4.5. Therefore 2/3 is a longer odds than 1/2 (it pays out more if you win).

And 7/5 is definitely longer than 1/2 (it’s “greater” than 1/1 whereas 1/2 is “less” than 1/1).

Why is it not correct? Most bookmakers here use fraction notation.

Think of it this way. If you bet £x you will earn £1.5x if you win. Now stake the same amount (£x) on the odds you’re looking at. If your earnings are more than £1.5x, then those odds are longer than 1/2. Otherwise they are shorter.

No, he’s phrasing it in a way I understand very well.

Why, of course! A concave decagon.

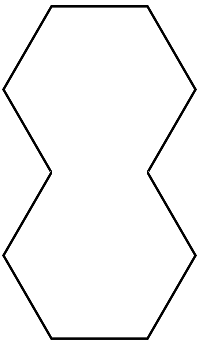
NB: I think I’ve proved that a regular concave polygon (i.e. a polygon with equal sides and internal angles either θ or 360°−θ, at least one of which is reflex) must have at least 9 sides. If my proof is correct, it remains to check whether there exists any regular concave nonagon.