Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#4026 Re: Help Me ! » Differential Equation » 2007-03-11 03:23:33
This is an equation of the form
I believe theres a standard method for solving it. (You know, the one involving particular integrals and complementary functions?)
EDIT: Er, I found the formula to use:
http://eqworld.ipmnet.ru/en/solutions/ode/ode0103.pdf
#4027 Re: Help Me ! » LaTeX - A Crash Course » 2007-03-11 03:10:12
Ive just learnt a handy little trick. You can use the double-dollar $$ to make part of your text smaller. For example, if you type
\cos{x}=0\Leftrightarrow x\in\{(n+\frac{1}{2})\pi:n\in\mathbb{Z}\}
you get
It looks fine except that the fraction appears a little oversized in the formula. To make it smaller and the formula neater, put $$ before and after the code for the fraction:
\cos{x}=0\Leftrightarrow x\in\{(n+$$\frac{1}{2}$$)\pi:n\in\mathbb{Z}\}
#4028 Re: Help Me ! » Unproved theorems » 2007-03-11 02:28:57
Off the top of my head, Goldbachs conjecture:
#4029 Re: Exercises » Janes exercises » 2007-03-10 18:13:00
More exercises from me. ![]()
4. If x is real, what is 0[sup]x[/sup]?
5. If x is a real number, [x] denotes the greatest integer less than or equal x. Prove that for any real numbers x and y,
In other words, the greatest-integer function is a superadditive function. (Hint: If n is any integer such that n ≤ x, then n ≤ [x].)
6. A cycloid is the curve traced by a fixed point on a circle rolling along a straight line. If the radius of the generating circle is r, the parametric equations of the cycloid are
Find the area bounded by one arch of the generated curve (0 ≤ θ ≤ 2π) and the x-axis.
#4030 Re: Help Me ! » Proof » 2007-03-10 14:07:35
It was just a query about X; I deleted it as Sekkys post appeared to have answered the question. ![]()
#4031 Re: Help Me ! » Differential Equation » 2007-03-10 11:58:59
Thats what Ive got as well. ![]()
Since
you can also write the answer as
#4032 Re: Help Me ! » Differential Equation » 2007-03-10 11:20:52
This differential equation is of the variables-separable type. You can separate the variables and integrate.
#4033 Re: Puzzles and Games » Words words words! » 2007-03-10 11:13:24
#4034 Re: Help Me ! » Lemniscate » 2007-03-10 11:05:49
Normally, students are asked to derive the Cartesian equation from the parametric ones, not the other way round. ![]()
To get a set of parametric equations from the Cartesian one, you can choose x to be some function of t, and then express y in terms of t. The function of t you choose for x is usually such as to yield simple expressions for x and y. The parametric equations for any curve are not unique.
For example, as parametric equations for the straight line y = mx + c (m ≠ 0), you can simply choose x = t, so y = mt + c. You can also chosse x = t/m, y = t + c as your parametric equations instead. Or you can even choose x = t/m−c/m, y = t. There is no one fixed choice.
#4035 Re: Help Me ! » Need to know how? » 2007-03-10 04:25:17
The dynamic coin is rolling along the circumference of the static coin, if thats what you mean? In that case, the dynamic coin will make two revolutions for each complete roll around the static coin.
Try it with real coins and test it for yourself. ![]()
#4036 Re: Help Me ! » Whats the perimeter? » 2007-03-10 04:09:01
Refer to Toasts diagram. The angle θ in the diagram is π⁄3 radians. Twice that is 2π⁄3 radians. So the length of the arc subtending this angle (one vertical half of the lime curve in Toasts diagram) is (2π⁄3)r. (Get it? If not, read up on the definition of the radian. ![]() )
)
∴ The perimeter of C (i.e. length of the lime curve in Toasts diagram) is 2×(2π⁄3)r = (2π⁄3)d = . Thats my answer (same as Toasts). ![]()
#4037 Re: Help Me ! » Help! » 2007-03-10 03:22:35
Its quite straightforward, really. Plot the graphs to see what sort of the area you need to calculate. Determine the relevant points of intersection, and then calculate the area. ![]()
#4038 Re: Help Me ! » gradient and y-intercept » 2007-03-09 12:26:01
1. When you have a line whose equation is y = mx + c, m is the gradient and c is the y-intercept. For example, for the line given by y = 2x + 3, the gradient is 2 and the y-intercept is 3 (i.e. it passes through the point (0.3)).
If a line passes through the points (a,b) and (c,d), the gradient of the line is (b−d)∕(a−c).
In your example, your line passes through (4.0) and (0,−1). The gradient is therefore (0−(−1))∕(4−0) = 1⁄4.
Since the line passes through (0,−1), the y-intercept is −1.
So the equation of your line is y = {gradient}x + {y-intercept} = (1⁄4)x − 1.
2. If the equation you are given is not in the form y = mx + c, you must write it in that form so the gradient can be read. For example, if you are given x + y = 4 , you must re-write it as y = −x + 4; then you can see that the gradient is −1.
(a) In your example, (i) is already in the form y = mx + c. You can read the gradient straightaway. (ii) is not, so you must re-write it in the form y = mx + c.
(b) If two straight lines do not intersect, that means they are parallel. Parallel lines have the same gradient. Thus, if you have a line with equation y = mx + c and another line with equation y = mx + d, and c ≠ d, then the two lines are parallel; they will never intersect.
I hope you can digest all this. ![]() If not, read it through slowly, bit by bit.
If not, read it through slowly, bit by bit.
#4039 Re: Help Me ! » need help » 2007-03-09 10:08:11
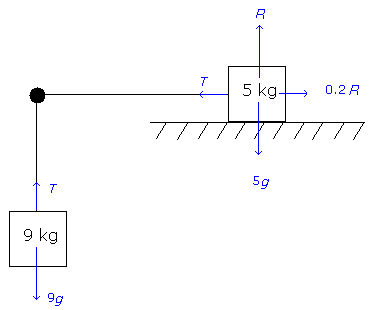
Let the tension in the string be T.
The acceleration for both blocks is the same; let it be a. Then the net vertical force on the 9kg block is 9a and the net horizontal force on the 5kg block is 5a.
From the diagram,
and
Hence
Now you can solve for T (taking g = 9.8 ms[sup]−2[/sup]).
#4040 Re: Puzzles and Games » Triangles - Squares » 2007-03-09 03:42:26
Im not sure but Ill say
#4041 Re: Puzzles and Games » Words words words! » 2007-03-08 10:14:45
#4042 Re: Dark Discussions at Cafe Infinity » I wrote this song this morning. » 2007-03-08 10:05:40
So, is this how its supposed to sound (at crotchet=120)?
http://homepage.ntlworld.com/george.law7/GPN.mid
I made the MIDI file using NoteWorthy Composer, by the way.
#4043 Re: Puzzles and Games » Spot the error » 2007-03-08 06:53:54
Exactly mathsyperson! ![]()
The correct statement should be
.Now your turn to post a false proof. ![]()
#4044 Re: Help Me ! » What is 7+9? » 2007-03-08 06:50:29
Its a riddle. Seven ate nine.
#4045 Re: This is Cool » Trick to finding multiples of 3 » 2007-03-08 05:47:11
i dont quite get how tihs works...
Lets take an example: 314159265
Add the digits: 3 + 1 + 4 + 1 + 5 + 9 + 2 + 6 + 5 = 36
Add the digits of the resulting sum: 3 + 6 = 9
(You keep adding the digits of the resulting sums until you get a single-digit number.)
9 is a multiple of 3.
∴ 314159265 is a multiple of 3.
Another example: 2718281828
Add the digits: 2 + 7 + 1 + 8 + 2 + 8 + 1 + 8 + 2 + 8 = 47
Add again: 4 + 7 = 11
And again: 1 + 1 = 2
2 is not a multiple of 3.
2718281828 is not a multiple of 3.
And mathsyperson, yes: 0 is a multiple of 3. An integer a is a multiple of an integer b iff a = bc for some integer c; since 0 = 3×0, 0 is thus a multiple of 3. ![]()
#4046 Re: Puzzles and Games » Spot the error » 2007-03-08 04:45:52
Nope, thats not it. Look closely at the equations again. ![]()
#4047 Re: Jokes » Good Jokes Pt III » 2007-03-08 03:02:17
OMG, thats too funny! 
#4048 Re: Help Me ! » division » 2007-03-07 17:17:04
I got it.
Now apply Wilsons theorem and the result should follow.
#4049 Re: Jai Ganesh's Puzzles » 5 Star Questions » 2007-03-07 16:40:49
#4050 Re: Help Me ! » What is the answer? » 2007-03-07 16:23:18
If two concentric circles have radii r[sub]1[/sub] and r[sub]2[/sub] (r[sub]1[/sub] < r[sub]2[/sub]), the area of the ring in between (called an annulus) is π(r[sub]2[/sub][sup]2[/sup]−r[sub]1[/sub][sup]2[/sup]).
And ganesh, the 17.5 is wrong it should be 12.5.