Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 Re: Exercises » Compute the solution: » Today 00:16:19
Hi,
2687.
#2 Re: Jai Ganesh's Puzzles » 10 second questions » Yesterday 23:55:19
Hi,
#9836.
#3 Re: Jai Ganesh's Puzzles » Oral puzzles » Yesterday 23:40:52
Hi,
#6330.
#4 Re: Exercises » Compute the solution: » Yesterday 23:05:33
Hi,
2687.
#5 Dark Discussions at Cafe Infinity » Color Quotes - II » Yesterday 22:33:54
- Jai Ganesh
- Replies: 0
Color Quotes - II
1. To me, the good thing about living in L.A. is diversity in lifestyle choices, color, and religion. - Sandra Bullock
2. In inner-city, low-income communities of color, there's such a high correlation in terms of educational quality and success. - Bill Gates
3. She said the object and color in the materials around us actually have a physical effect on us, on how we feel. - Florence Nightingale
4. In too many communities, too many young men of color are left behind and seen only as objects of fear. Through initiatives like My Brother's Keeper, I'm personally committed to changing both perception and reality. - Barack Obama
5. Here's the thing: every office I've run for I was the first to win. First person of color. First woman. First woman of color. Every time. - Kamala Harris
6. I was always shocked when I went to the doctor's office and they did my X-ray and didn't find that I had eight more ribs than I should have or that my blood was the color green. - Nicolas Cage
7. The over-all point is that new technology will not necessarily replace old technology, but it will date it. By definition. Eventually, it will replace it. But it's like people who had black-and-white TVs when color came out. They eventually decided whether or not the new technology was worth the investment. - Steve Jobs
8. I believe there is complete equality between men and women. And I believe those passages in the New Testament, not by Jesus, but by Paul, that say women should not adorn themselves, they should always wear hats or color their hair in church - things like that - I think they are signs of the times and should not apply to modern-day life. - Jimmy Carter.
#6 Jokes » Chocolate Jokes - I » Yesterday 22:15:43
- Jai Ganesh
- Replies: 0
Q: What kind of candy is never on time?
A: ChocoLATE.
* * *
Q: What are the 4 major food groups? Pizza, Coffee, Chocolate and Tea.
* * *
Q: What do cannibals eat for dessert?
A: Chocolate covered aunts.
* * *
Q: How does the recipe for German chocolate cake begin?
A: First, invade ze kitchen.
* * *
Q: If Jake has 30 chocolate bars, and eats 25, what does he have?
A: Diabetes..... Jake has diabetes...
* * *
#7 Re: This is Cool » Miscellany » Yesterday 18:24:37
2479) Greenland Shark
Greenland Shark
Gist
Greenland sharks (Somniosus microcephalus) are the longest-lived vertebrates on Earth, with lifespans estimated between 250 and 500 years. A 2016 study using radiocarbon dating of eye lens proteins indicated they live at least 272 years, with some individuals estimated to be roughly 400 years old, and possibly up to 512 years.
The Greenland shark has the longest known lifespan of all vertebrate species. It is estimated that the species has a lifespan of at least 272 years, with the oldest individual estimated to be 392 ± 120 years of age.
Summary
Greenland sharks are now the longest-living vertebrates known on Earth, scientists say.
Researchers used radiocarbon dating to determine the ages of 28 of the animals, and estimated that one female was about 400 years old.
The team found that the sharks grow at just 1cm a year, and reach sexual maturity at about the age of 150.
The research is published, external in the journal Science.
Lead author Julius Nielsen, a marine biologist from the University of Copenhagen, external, said: "We had our expectations that we were dealing with an unusual animal, but I think everyone doing this research was very surprised to learn the sharks were as old as they were."
The former vertebrate record-holder was a bowhead whale estimated to be 211 years old.
But if invertebrates are brought into the longevity competition, a 507-year-old clam called Ming, external holds the title of most aged animal.
Slow swimmers
Greenland sharks are huge beasts, that can grow up to 5m in length.
They can be found, swimming slowly, throughout the cold, deep waters of the North Atlantic.
With this leisurely pace of life and sluggish growth rate, the sharks were thought to live for a long time. But until now, determining any ages was difficult.
For some fish, scientists are able to examine ear bones called otoliths, which when sectioned, show a pattern of concentric rings that scientists can count as they would the rings in a tree.
Sharks are harder, but some species, such as the Great White, have calcified tissue that grows in layers on their back bones, that can also be used to age the animals.
"But the Greenland shark is a very, very soft shark - it has no hard body parts where growth layers are deposited. So it was believed that the age could not be investigated," Mr Nielsen told the BBC.
However the team found a clever way of working out the age.
"The Greenland shark's eye lens is composed of a specialised material - and it contains proteins that are metabolically inert," explained Mr Neilson.
"Which means after the proteins have been synthesised in the body, they are not renewed any more. So we can isolate the tissue that formed when the shark was a pup, and do radiocarbon dating."
The team looked at 28 sharks, most of which had died after being caught in fishing nets as by-catch.
Using this technique, they established that the largest shark - a 5m-long female - was extremely ancient.
Because radiocarbon dating does not produce exact dates, they believe that she could have been as "young" as 272 or as old as 512. But she was most likely somewhere in the middle, so about 400 years old.
It means she was born between the years of 1501 and 1744, but her most likely date of birth was in the 17th century.
"Even with the lowest part of this uncertainty, 272 years, even if that is the maximum age, it should still be considered the longest-living vertebrate," said Mr Nielsen.
Conversely, if her age is at the upper end of the scale, she will have out-lived Ming the clam - although her age has a greater probability of lying in the middle.
Details
The Greenland shark (Somniosus microcephalus), also known as the rubiks shark or gray shark, is a large shark of the family Somniosidae ("sleeper sharks"), closely related to the Pacific and southern sleeper sharks. Inhabiting the North Atlantic and Arctic Oceans, they are notable for their exceptional longevity, although they are poorly studied due to the depth and remoteness of their natural habitat.
Greenland sharks have the longest lifespan of any known vertebrate, estimated to be between 250 and 500 years. They are among the largest extant shark species, reaching a maximum confirmed length of 6.4 m (21 ft) and weighing more than 1,000 kg (2,200 lb). They reach sexual maturity around 150 years of age and their pups are born alive after an estimated gestation period of 8 to 18 years. The shark is a generalist feeder, consuming a variety of available foods, including carrion.
Greenland shark meat is toxic to mammals due to its high levels of trimethylamine N-oxide, although a treated form of it is eaten in Iceland as a delicacy known as kæstur hákarl. Because they live deep in remote parts of the northern oceans, Greenland sharks are not considered a threat to humans. A possible attack occurred in August 1936 on two British fishermen, but the species was never identified.
Description
The Greenland shark is one of the largest known existing species of shark, with adults growing to around 4 to 5 m (13 to 16 ft). The largest confirmed specimen measured up to 6.4 metres (21 ft) long and weighed around 1,023 kilograms (2,255 lb). The all-tackle International Game Fish Association (IGFA) record for this species is 775 kg (1,709 lb). It rivals the Pacific sleeper shark (possibly up to 7 m or 23 ft long) for the largest species in the family Somniosidae. Genetic data indicate that Greenland sharks diverged from ancestral sleeper sharks in the Canadian Arctic approximately 1–2.34 million years ago during the Pleistocene epoch, likely influenced by glacial fluctuations that periodically isolated marine populations. These ecological challenges may have driven physiological and metabolic adaptations for cold, deep waters.
The Greenland shark is a thickset species, with a short, rounded snout, small eyes, and small dorsal and pectoral fins. The gill openings are very small for the species's great size. Females are typically larger than males, with males reaching maturity at a smaller size than females.
Coloration can range from pale creamy-gray to blackish-brown and the body is typically uniform in color, though whitish spots or faint dark streaks are occasionally seen on the back.
The shark is often infested by the copepod Ommatokoita elongata, a crustacean that attaches itself to the shark's eyes. The copepod may display bioluminescence, thus attracting prey for the shark in a mutualistic relationship, but this hypothesis has not been verified. These parasites can cause multiple forms of damage to the sharks' eyes, such as ulceration, mineralization, and edema of the cornea, leading to almost complete blindness. This does not seem to reduce the life expectancy or predatory ability of Greenland sharks, due to their strong reliance on smell and hearing.
The genome of the Greenland shark was published in 2024. It is 6.45 billion base pairs in length.
Dentition
The dentition of a Greenland shark:
When feeding on large carcasses, the shark employs a rolling motion of its jaw. The 48 to 52 teeth of the upper jaw are very thin and pointed, lacking serrations. These upper jaw teeth act as an anchor, while the lower jaw proceeds to cut massive chunks out of the prey.
The 48 to 52 lower teeth interlock, are broad and square in shape, and contain short, smooth cusps that point outward. Teeth in the two halves of the lower jaw are strongly pitched in opposite directions.
Physiology
Like other Elasmobranchii, Greenland sharks have high concentrations of the two nitrogenous compounds urea and trimethylamine N-oxide (TMAO) in their tissues, which increase their buoyancy and function as osmoprotectants. TMAO also counteracts the protein-destabilizing tendencies of urea and deep-water pressure. Its presence in the tissues of both elasmobranch and teleost fish has been found to increase with depth.
The blood of Greenland sharks contains three major types of hemoglobin, made up of two copies of α globin combined with two copies of three very similar β subunits. These three types show very similar oxygenation and carbonylation properties, which are unaffected by urea, an important compound in marine Elasmobranchii physiology. They display identical electronic absorption and resonance in Raman spectroscopy, indicating that their heme-pocket structures are identical or highly similar. The hemoglobins also have a lower affinity for oxygen compared to those of temperate sharks. These characteristics are believed to be adaptations to living at great depths.
When hoisted upon deck, it beats so violently with its tail, that it is dangerous to be near it, and the seamen generally dispatch it, without much loss of time. The pieces that are cut off exhibit a contraction of their muscular fibres for some time after life is extinct. It is, therefore, extremely difficult to kill, and unsafe to trust the hand within its mouth, even when the head is cut off. And, if we are to believe Crantz, this motion is to be observed three days after, if the part is trod on or struck.
— Henry William Dewhurst, The Natural History of the Order Cetacea (1834).
Additional Information
Greenland shark, (Somniosus microcephalus), member of the sleeper shark family Somniosidae (order Squaliformes, which also includes the dogfish family, Squalidae) also known for being the world’s longest-lived vertebrate. The species is primarily found in the cold-water environments of the Arctic Ocean and North Atlantic, from Baffin Bay eastward to the Barents Sea, but its range also extends southward to the North Sea and the waters adjacent to the Eastern Seaboard of the United States. Bulky, with a rounded snout, small fins relative to body size, and gray to brown coloration, Greenland sharks are similar to spiny dogfish (Squalus acanthias), except that they lack a spine in front of the second dorsal fin and usually the one on the first dorsal fin.
Natural history
The Greenland shark is one of the largest cartilaginous fishes. It can reach a length of 7 metres (23 feet) and a weight of 1,025 kg (2,260 pounds) when fully grown, but most are between 2 and 4 metres (6.5 and 13 feet). Little is known, however, about how the species reproduces. Females are thought to reach sexual maturity when they surpass the 4-metre (13-foot) mark in length, which takes approximately 150 years to achieve. They are ovoviviparous (that is, eggs are retained within the body until they hatch) and produce an average of 10 offspring at a time. The type, amount, and duration of parental care the young receive are unknown, but scientists speculate that, like other shark species, Greenland sharks are independent from birth. No other vertebrate known has a life span as long as this species, and a 2016 study that used radiocarbon dating to examine isotopes in the shark’s eye-lens nuclei suggested that the oldest Greenland sharks may be more than 500 years old. Using this technique, scientists estimated that the largest Greenland shark in the study was likely between 272 and 512 years old.
Greenland sharks are rarely encountered by humans. They are thought to prefer colder, deeper environments but may be found anywhere between the sea surface and depths of 2,200 meters (about 7,200 feet). Greenland sharks are slow-moving, typically swimming at rates of less than 3 km (about 1.9 miles) per hour.
They are carnivorous, and their diet is often made up of several different types of fishes, including smaller sharks, eels, flounders, and sculpins. Crustaceans, seabirds, and carrion—as well as terrestrial mammals (such as horses and reindeer) that likely fell through the ice—have been found in stomach analyses of the species. Greenland sharks are not considered dangerous to humans, in part because they live in regions where people do not typically swim; the only known report of a possible attack by a Greenland shark on a person dates to 1859.
Conservation status
The International Union for Conservation of Nature has classified the Greenland shark as a vulnerable species since 2020. The fish was valued historically for its liver oil; about 114 litres (30 gallons) of liver oil can be obtained from a large specimen (see also fish oil). (Although the flesh of the Greenland shark may be eaten, it is toxic unless properly cleaned and dried or repeatedly boiled prior to consumption.) They were fished commercially from the 19th century until 1960. Norway persecuted Greenland sharks during the 1970s, because they were considered to be a nuisance that threatened other fisheries. In the early 1900s as many as 30,000 Greenland sharks were caught a year. In the present day the annual take is far smaller; small-scale subsistence fisheries in the Arctic harvest fewer than 100 individuals annually, and roughly 1,200 are caught accidentally in fishing trawls.

#8 Science HQ » Pia Mater » Yesterday 16:20:50
- Jai Ganesh
- Replies: 0
Pia Mater
Gist
Pia mater, often referred to as simply the pia, is the delicate innermost layer of the meninges, the membranes surrounding the brain and spinal cord. Pia mater is medieval Latin meaning "tender mother". The other two meningeal membranes are the dura mater and the arachnoid mater.
The pia mater is the innermost layer of the meninges and together with the arachnoid mater is referred to as the leptomeninges. It is closely related to the surface of the brain and unlike the arachnoid mater extends into the sulci
The pia mater is the innermost layer of the meninges and together with the arachnoid mater is referred to as the leptomeninges. It is closely related to the surface of the brain and unlike the arachnoid mater extends into the sulci.
Summary
Pia is the innermost layer of the meninges, the connective tissue layers that surround the central nervous system. It is a thin, transparent, delicate layer that hugs the surface of the brain and spinal cord, closely following its contours. The pia and arachnoid layers of the meninges are collectively called the leptomeninges. Located between these two layers is the cerebrospinal fluid containing subarachnoid space.
The pia is highly vascularized by a network of fine blood vessels. In the cranium, the pia extends for a short distance along the surface of blood vessels as they travel to and from the meninges to enter and exit the cerebral cortex. This pia extension is called a pial coat. Similar extensions are seen in the spinal cord where the pia follows spinal nerves and spinal blood vessels for a short distance as they travel away from the central cord. Fingers of vascularized pia covered by epithelial cells form invaginations into ventricles called choroid plexuses. Choroid plexuses function to secrete cerebrospinal fluid.
In the spinal cord, the pia forms tiny ligaments called the denticulate ligaments. These ligaments suspend the spinal cord within the dural sac. The inferior most aspect of the spinal meninges is anchored to the coccyx by a thin strand called the filum terminale. This filum has internal and external parts, the internal being formed by a strand of pia.
Details
Pia mater, often referred to as simply the pia, is the delicate innermost layer of the meninges, the membranes surrounding the brain and spinal cord. Pia mater is medieval Latin meaning "tender mother". The other two meningeal membranes are the dura mater and the arachnoid mater. Both the pia and arachnoid mater are derivatives of the neural crest while the dura is derived from embryonic mesoderm. The pia mater is a thin fibrous tissue that is permeable to water and small solutes. The pia mater allows blood vessels to pass through and nourish the brain. The perivascular space between blood vessels and pia mater is proposed to be part of a pseudolymphatic system for the brain (glymphatic system). When the pia mater becomes irritated and inflamed the result is meningitis.
Structure
Pia mater is the thin, translucent, mesh-like meningeal envelope, spanning nearly the entire surface of the brain. It is absent only at the natural openings between the ventricles, the median aperture, and the lateral aperture. The pia firmly adheres to the surface of the brain and loosely connects to the arachnoid layer. Because of this continuum, the layers are often referred to as the pia arachnoid or leptomeninges. A subarachnoid space exists between the arachnoid layer and the pia, into which the choroid plexus releases and maintains the cerebrospinal fluid (CSF). The subarachnoid space contains trabeculae, or fibrous filaments, that connect and bring stability to the two layers, allowing for the appropriate protection from and movement of the proteins, electrolytes, ions, and glucose contained within the CSF.
The thin membrane is composed of fibrous connective tissue, which is covered by a sheet of flat cells impermeable to fluid on its outer surface. A network of blood vessels travels to the brain and spinal cord by interlacing through the pia membrane. These capillaries are responsible for nourishing the brain. This vascular membrane is held together by areolar tissue covered by mesothelial cells from the delicate strands of connective tissue called the arachnoid trabeculae. In the perivascular spaces, the pia mater begins as mesothelial lining on the outer surface, but the cells then fade to be replaced by neuroglia elements.
Although the pia mater is primarily structurally similar throughout, it spans both the spinal cord's neural tissue and runs down the fissures of the cerebral cortex in the brain. It is often broken down into two categories, the cranial pia mater (pia mater encephali) and the spinal pia mater (pia mater spinalis).
Cranial pia mater
The section of the pia mater enveloping the brain is known as the cranial pia mater. It is anchored to the brain by the processes of astrocytes, which are glial cells responsible for many functions, including maintenance of the extracellular space. The cranial pia mater joins with the ependyma, which lines the cerebral ventricles to form choroid plexuses that produce cerebrospinal fluid. Together with the other meningeal layers, the function of the pia mater is to protect the central nervous system by containing the cerebrospinal fluid, which cushions the brain and spine.
The cranial pia mater covers the surface of the brain. This layer goes in between the cerebral gyri and cerebellar laminae, folding inward to create the tela chorioidea of the third ventricle and the choroid plexuses of the lateral and third ventricles. At the level of the cerebellum, the pia mater membrane is more fragile due to the length of blood vessels as well as decreased connection to the cerebral cortex.
Spinal pia mater
The spinal pia mater closely follows and encloses the curves of the spinal cord, and is attached to it through a connection to the anterior fissure. The pia mater attaches to the dura mater through 21 pairs of denticulate ligaments that pass through the arachnoid mater and dura mater of the spinal cord. These denticular ligaments help to anchor the spinal cord and prevent side to side movement, providing stability. The membrane in this area is much thicker than the cranial pia mater, due to the two-layer composition of the pia membrane. The outer layer, which is made up of mostly connective tissue, is responsible for this thickness. Between the two layers are spaces which exchange information with the subarachnoid cavity as well as blood vessels. At the point where the pia mater reaches the conus medullaris or medullary cone at the end of the spinal cord, the membrane extends as a thin filament called the filum terminale or terminal filum, contained within the lumbar cistern. This filament eventually blends with the dura mater and extends as far as the coccyx, or tailbone. It then fuses with the periosteum, a membrane found at the surface of all bones, and forms the coccygeal ligament. There it is called the central ligament and assists with movements of the trunk of the body.
Additional Information
The pia mater is the delicate innermost layer of the meninges, directly enveloping the brain and spinal cord and adhering closely to the contours of the central nervous system (CNS) surface, including the gyri and sulci of the brain and the external surfaces of the spinal cord. It is composed of connective tissue, including collagenous, reticular, and elastic fibers, and contains numerous blood vessels that penetrate the CNS parenchyma. The pia mater is covered superficially by a single layer of flattened mesothelial cells and is anchored to the underlying cortex by a glial membrane.
This meningeal layer plays a significant role in maintaining the neural microenvironment through its involvement in neurovascular interactions. It forms sheaths around blood vessels entering and exiting the CNS, creating perivascular spaces known as Virchow–Robin spaces. These spaces are important for cerebrospinal fluid (CSF) absorption and clearance and are thought to communicate with the subpial space. The pia mater is continuous with the glia limitans, a thin subpial layer comprised of astrocyte endfeet, which insulates the CNS from substances present in the vascular and subarachnoid compartments. The subarachnoid space, located between the arachnoid mater and the pia mater, contains CSF, which circulates and provides mechanical protection, nutrient delivery, and waste removal for the CNS.

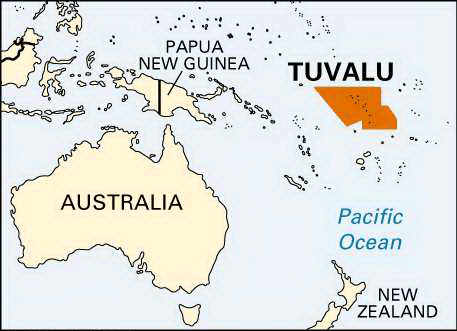
#9 This is Cool » Tuvalu » Yesterday 15:49:39
- Jai Ganesh
- Replies: 0
Tuvalu
Gist
Tuvalu is a low-lying Polynesian island nation in the west-central Pacific, known for its nine coral atolls and islands, rich marine life, and significant threat from rising sea levels due to climate change. An independent Commonwealth realm, it's economically reliant on fishing licenses, remittances, stamps, the ".tv" domain, and aid, with its capital and main government hub on Funafuti. The culture emphasizes strong community ties, while its low elevation makes it a focal point for global climate action discussions.
Nobody visits Tuvalu much because it's incredibly remote, hard to reach due to limited flights, lacks large-scale tourist resorts, and faces serious threats from rising sea levels and climate change, despite its pristine beauty, making it the world's least-visited country. Its tiny size, scarce infrastructure, and isolation combine to make it logistically challenging and expensive for most tourists to access.
Summary
Tuvalu is an island country in the Polynesian sub-region of Oceania in the Pacific Ocean, about midway between Hawaii and Australia. It lies east-northeast of the Santa Cruz Islands (which belong to the Solomon Islands), northeast of Vanuatu, southeast of Nauru, south of Kiribati, west of Tokelau, northwest of Samoa and Wallis and Futuna, and north of Fiji.
Tuvalu is composed of three reef islands and six atolls spread out between the latitude of 5° and 10° south and between the longitude of 176° and 180°. They lie west of the International Date Line. The 2022 census determined that Tuvalu had a population of 10,643, making it the 194th most populous country, exceeding only Niue and the Vatican City in population. Tuvalu's total land area is 25.14 square kilometres (9.71 sq mi).
The first inhabitants of Tuvalu were Polynesians arriving as part of the migration of Polynesians into the Pacific that began about three thousand years ago. Long before European contact with the Pacific islands, Polynesians frequently voyaged using canoes between the islands. Polynesian navigation skills enabled them to make elaborately planned journeys in either double-hulled sailing canoes or outrigger canoes. Scholars believe that the Polynesians spread out from Samoa and Tonga into the Tuvaluan atolls, which then served as a stepping stone for further migration into the Polynesian outliers in Melanesia and Micronesia.
In 1568, Spanish explorer and cartographer Álvaro de Mendaña became the first European known to sail through the archipelago, sighting the island of Nui during an expedition he was making in search of Terra Australis. The island of Funafuti, currently serving as the capital, was named Ellice's Island in 1819. Later, the whole group was named Ellice Islands by English hydrographer Alexander George Findlay. In the late 19th century, Great Britain claimed control over the Ellice Islands, designating them as within their sphere of influence. Between 9 and 16 October 1892, Captain Herbert Gibson of HMS Curacoa declared each of the Ellice Islands a British protectorate. Britain assigned a resident commissioner to administer the Ellice Islands as part of the British Western Pacific Territories (BWPT). From 1916 to 1975, they were managed as part of the Gilbert and Ellice Islands colony.
A referendum was held in 1974 to determine whether the Gilbert Islands and Ellice Islands should each have their own administration. As a result, the Gilbert and Ellice Islands colony legally ceased to exist on 1 October 1975; on 1 January 1976, the old administration was officially separated, and two separate British colonies, Kiribati and Tuvalu, were formed. On 1 October 1978, Tuvalu became fully independent as a sovereign state within the Commonwealth, and is a constitutional monarchy with Charles III as King of Tuvalu. On 5 September 2000, Tuvalu became the 189th member of the United Nations.
The islands do not have a significant amount of soil, so the country relies heavily on imports and fishing for food. Licensing fishing permits to international companies, grants and aid projects, and remittances to their families from Tuvaluan seafarers who work on cargo ships are important parts of the economy. Because it is a low-lying island nation, Tuvalu is extremely vulnerable to sea level rise due to climate change. It is active in international climate negotiations as part of the Alliance of Small Island States.
Details
Tuvalu, country in the west-central Pacific Ocean. It is composed of nine small coral islands scattered in a chain lying approximately northwest to southeast over a distance of some 420 miles (676 km).
The de facto capital is the village of Vaiaku, where most government offices are located. It is on Fongafale islet, a constituent part of Funafuti Atoll. Together with what is now Kiribati (formerly the Gilbert Islands), Tuvalu formed the British Gilbert and Ellice Islands Colony before separately gaining its independence in 1978.
Land
The group includes both atolls and reef islands. The atolls—Nanumea, Nui, Nukufetau, Funafuti, and Nukulaelae—have islets encircling a shallow lagoon; the reef islands—Nanumanga, Niutao, Vaitupu, and Niulakita—are compact with a fringing reef. The islands are low-lying, most being 13 to 16 feet (4 to 5 meters) above sea level. There are no rivers; rain catchment and wells provide the only fresh water. Rainfall averages 100 inches (2,500 mm) in the north and 125 inches (3,175 mm) in the south. The prevailing winds are southeast trades; westerly storms occur from November to February. Daytime temperatures range from 80 to 85 °F (27 to 29 °C).
Because the soils are porous, agriculture is limited. Coconut palms thrive, and breadfruit trees, pandanus, taro, and bananas are grown. Pigs and chickens are raised, and seabirds, fish, and shellfish are caught for food. The islands increasingly depend on imported food.
People
The Tuvaluans are Polynesian, and their language, Tuvaluan, is closely related to Samoan. Nui, however, was heavily settled in prehistoric times by Micronesians from the Gilbert Islands (now Kiribati). English is taught in the schools and widely used. The vast majority of the population belongs to the Church of Tuvalu (the former Ellice Islands Protestant Church).
Although most people live on the outer islands in extended family households clustered into villages, about one-third of the population lives on Funafuti, the center of government and commerce. Population growth has been slowed by family planning; life expectancy at birth is about 60 years. About 10 percent of the population lives overseas, either pursuing education, working in the Nauru phosphate industry, or working on merchant ships.
Economy
Most Tuvaluans are subsistence farmers and are aided by remittances from relatives working overseas. A small quantity of copra is produced for export, the sale of stamps accounts for modest earnings, and fees are collected from foreign fishing fleets, but the country depends heavily on foreign aid. It imports most of its food, fuel, and manufactured goods. Fiji, Australia, New Zealand, and Japan are among the country’s major trade partners. Retailing is handled by community-based cooperative societies. Tuvalu uses Australian currency but also issues its own coinage. There is a single bank, a joint government-commercial venture.
Tuvalu has air links with Kiribati and Fiji; for international shipping, it depends on irregular regional services. Seaplanes have been used for interisland travel, but generally the outer islands depend on a single government vessel. Motorcycles are common on Funafuti, but there are few automobiles.
Government and society
Tuvalu is a constitutional monarchy within the Commonwealth, with the British monarch (through a governor-general) as head of state. The government is a parliamentary democracy with a unicameral legislature elected by universal adult suffrage. There are no political parties: the prime minister is chosen by and from the legislature. Tuvalu is a member of the South Pacific Forum.
The government provides universal primary education and, under a joint arrangement with the Church of Tuvalu, secondary education to school certificate level for selected pupils. A few are sent overseas for further education and training. Medical facilities are centralized on Funafuti, but all other islands have clinics with trained medical staff.
Cultural life
The Tuvaluan lifestyle has been Westernized to an extent, but Western-style amenities are few. Only Funafuti has a regular electricity supply; the government publishes a brief news sheet, but there is no newspaper; a few motion pictures are shown; satellite television service is available only by subscription; and there is only a single radio station. Most Tuvaluans live in villages of a few hundred people, tend their gardens, and fish from handcrafted canoes. Traditional music and dancing still enjoy a strong following, along with Western forms. Volleyball, football (soccer), and cricket are popular. Tuvaluan life, despite modernization, still rests on a firm traditional base that emphasizes the importance of community consensus and identity.
History of Tuvalu
The first settlers were from Samoa and probably arrived in the 14th century ad. Smaller numbers subsequently arrived from Tonga, the northern Cook Islands, Rotuma, and the Gilbert Islands. Niulakita, the smallest and southernmost island, was uninhabited before European contact; the other islands were settled by the 18th century, giving rise to the name Tuvalu, or “Cluster of Eight.”
Europeans first discovered the islands in the 16th century through the voyages of Álvaro de Mendaña de Neira, but it was only from the 1820s, with visits by whalers and traders, that they were reliably placed on European charts. In 1863 labor recruiters from Peru kidnapped some 400 people, mostly from Nukulaelae and Funafuti, reducing the population of the group to less than 2,500. A few were later recruited for plantations in Queensland, Australia, as well as in Fiji, Samoa, and Hawaii. Concern over labor recruiting and a desire for protection helps to explain the enthusiastic response to Samoan pastors of the London Missionary Society who arrived in the 1860s. By 1900, Protestant Christianity was firmly established.
With imperial expansion the group, then known as the Ellice Islands, became a British protectorate in 1892 and part of the Gilbert and Ellice Islands Colony in 1916. There was a gradual expansion of government services, but most administration was through island governments supervised by a single district officer based in Funafuti. Ellice Islanders sought education and employment at the colonial capital in the Gilbert group or in the phosphate industry at Banaba or Nauru. During World War II, U.S. forces were based on Nanumea, Nukufetau, and Funafuti, but hostilities did not reach the group.
From the 1960s, racial tension and rivalries over employment emerged between Gilbertese and Ellice Islanders. Ellice Islanders’ demands for secession resulted in a referendum in 1974, transition to separate colonial status between October 1975 and January 1976, and independence as Tuvalu in 1978. After independence the main priorities were to establish the infrastructure for a separate, if small, nation, and to seek foreign assistance to match political independence with economic viability.
Additional Information
Tuvalu is a small island nation located in the Pacific Ocean, composed of nine islands and atolls. It is known for its stunning natural beauty, including pristine beaches and rich marine biodiversity. The country has a population of around 11,000 people, who primarily engage in subsistence farming and fishing. Tuvalu faces significant challenges related to climate change, particularly rising sea levels, which threaten its very existence and have garnered international attention. The culture of Tuvalu is deeply rooted in Polynesian traditions, with a strong emphasis on community and family ties. The official languages are Tuvaluan and English, reflecting its colonial history and modern connections. Economically, Tuvalu relies on fishing, remittances from citizens abroad, and tourism, though it remains one of the least developed countries globally. Its unique cultural heritage, combined with pressing environmental concerns, makes Tuvalu a focal point for discussions on sustainability and climate action.
Tuvalu is a small independent island nation in the South Pacific (Oceania) consisting of nine low-lying coral atolls and reef islands. With a population of roughly 10,600 as of 2026, it is one of the world's smallest nations, heavily reliant on fishing, tourism, foreign aid, and the .tv internet domain. The capital is Funafuti, and the nation faces severe climate change threats.
#10 Dark Discussions at Cafe Infinity » Color Quotes - I » 2026-01-24 20:58:08
- Jai Ganesh
- Replies: 0
Color Quotes - I
1. Clouds come floating into my life, no longer to carry rain or usher storm, but to add color to my sunset sky. - Rabindranath Tagore
2. Design is the fundamental soul of a man-made creation that ends up expressing itself in successive outer layers of the product or service. The iMac is not just the color or translucence or the shape of the shell. The essence of the iMac is to be the finest possible consumer computer in which each element plays together. - Steve Jobs
3. Until justice is blind to color, until education is unaware of race, until opportunity is unconcerned with the color of men's skins, emancipation will be a proclamation but not a fact. - Lyndon B. Johnson
4. My favorite color is black. - Johnny Depp
5. I have dreamed in my life, dreams that have stayed with me ever after, and changed my ideas; they have gone through and through me, like wine through water, and altered the color of my mind. - Emily Bronte
6. If you're white and you're wrong, then you're wrong; if you're black and you're wrong, you're wrong. People are people. Black, blue, pink, green - God make no rules about color; only society make rules where my people suffer, and that why we must have redemption and redemption now. - Bob Marley
7. If they ever do my life story, whoever plays me needs lots of hair color and high heels. - Charlize Theron
8. Hating people because of their color is wrong. And it doesn't matter which color does the hating. It's just plain wrong. - Muhammad Ali.
#11 Jokes » Cherry Jokes - IV » 2026-01-24 20:40:11
- Jai Ganesh
- Replies: 0
Q: What does a cherry say at the end of the year?
A: Cherry Christmas.
* * *
Q: What did the cherry say to the cherry pie?
A: "You've got some crust."
* * *
Q: What happens when a cherry tree grows up?
A: It blossoms.
* * *
Q: What do you say when someone offers you some pie?
A: Thank you cherry much.
* * *
Q: What did Jani Lane tell Tommy Lee?
A: She's my cherry pie....
* * *
Q: What do you get when you cross a talk show host and a fruit?
A: Cherry Shepherd.
* * *
#12 Re: This is Cool » Miscellany » 2026-01-24 20:23:21
2478) Channel Tunnel
Channel Tunnel
Gist
The Channel Tunnel (often called the 'Chunnel' for short) is an undersea tunnel linking southern England and northern France. It is operated by the company Getlink, who also run a railway shuttle (Le Shuttle) between Folkestone and Calais, carrying passengers in cars, vans and other vehicles.
Which country owns the Channel tunnel?
To be specific, LeShuttle is operated by Getlink, the company which owns and operates the Channel Tunnel, the infrastructure connecting the UK with France. Eurostar is a customer of Getlink and runs its passenger trains through the tunnel.
How long are you underwater in the chunnel?
How long are you underwater on the Eurostar? It takes around 35 minutes for the Eurostar to cross the 23-mile underwater stretch of the Channel Tunnel.
Summary
The Channel Tunnel (French: Tunnel sous la Manche, sometimes referred to as the Chunnel) is a 50.46-kilometre (31.35-mile) railway tunnel beneath the English Channel that connects Folkestone in the United Kingdom with Coquelles in northern France. Opened in 1994, it remains the only fixed link between Great Britain and the European mainland.
The tunnel has the longest underwater section of any tunnel in the world, at 37.9 km (23.5 miles), reaching a depth of 75 m (246 ft) below sea level and runs, on average, 45 m (148 ft) below the seabed. It is the third-longest railway tunnel in the world. Although the tunnel was designed for speeds up to 200 km/h (120 mph), trains are limited to a maximum speed of 160 km/h (99 mph) for safety reasons. It connects to high-speed railway lines on either end: the LGV Nord in France and High Speed 1 in the United Kingdom.
The tunnel is operated by Getlink (formerly Eurotunnel) and is used by Eurostar high-speed passenger trains, LeShuttle services for road vehicles, and freight trains. In 2017, Eurostar trains carried 10.3 million passengers, freight trains transported 1.2 million tonnes (2.6 billion pounds) of freight, and LeShuttle trains moved 10.4 million passengers in 2.6 million cars and 51,000 coaches, and 1.6 million heavy goods vehicles carrying 21.3 million tonnes (47 billion pounds) of freight. That compares with 11.7 million passengers, 2.2 million cars, and 2.6 million heavy goods vehicles transported by sea through the Port of Dover.
Proposals for a cross-Channel tunnel date back as early as 1802, but concerns over national security delayed development. The modern project was initiated by Eurotunnel in 1988 and completed in 1994, at a final cost of £4.65 billion (equivalent to £11.7 billion in 2023). An engineering marvel, the Channel Tunnel was, at the time of its opening, by far the longest tunnel in Europe, and has only been surpassed by the Gotthard Base Tunnel in Switzerland. However, despite its engineering significance, several economic assessments have found that it has had only a limited positive economic impact on the British economy. Additionally, the tunnel has also experienced occasional service disruptions due to technical faults, fires, severe weather, and unauthorised access by migrants around Calais seeking entry to the United Kingdom.
Details
The Channel Tunnel (often called the 'Chunnel' for short) is an undersea tunnel linking southern England and northern France. It is operated by the company Getlink, who also run a railway shuttle (Le Shuttle) between Folkestone and Calais, carrying passengers in cars, vans and other vehicles.
Eurostar is a totally separate company and is Getlink’s biggest customer, running high-speed passenger services through the Channel Tunnel between London and a number of other European cities on the continent, including Paris, Brussels, Lille, Amsterdam and Rotterdam.
The Chunnel actually comprises three tunnels: two rail tunnels, used for freight and passenger trains, and a service tunnel.
How long is the Channel Tunnel?
The Channel Tunnel is 31.5 miles long or 50.45 km. That's the equivalent of 169 Eiffel Towers stacked on top of each other.
23.5 miles (37.9 km) of the Channel Tunnel is under the English Channel, making it the world's longest undersea tunnel.
What year did the Channel Tunnel open?
The idea of a tunnel under the Channel was first proposed in 1802 but construction wasn't started until 1988. It was completed in 1993, and Eurostar services started in November 1994.
What does the Eurotunnel look like underwater?
This may be a disappointing answer, but you can't actually see the sea from the Eurostar. When you go through the tunnel and look out of the window, all you can see is your reflection in the glass because it's quite dark outside. You can catch glimpses of the walls of the tunnel, of course, which are made of reinforced concrete.
Where is the Channel Tunnel?
The Channel Tunnel runs between Calais in northern France and Folkestone in south Kent. Vehicle traffic for Le Shuttle gets on in Calais and gets off in Folkestone. Calais is about three hour's drive from Paris and Folkestone is about an hour and a half's drive from London.
Our passenger-only Eurostar trains leave from St Pancras International station in London and go directly to the centre of Paris, Brussels and other Eurostar destinations in Europe.
How deep is the Channel Tunnel?
At its deepest, the tunnel is 75 metres (246 feet) below the sea level. That's the same as 107 baguettes balancing on top of each other.
The English Channel is much deeper than the tunnel, with its deepest point measuring 175 meters (574 feet) below sea level.
How was the Channel Tunnel built?
The Channel Tunnel is made of three separate tunnels running parallel to each other. One train tunnel running south (UK to France), one train tunnel running north (France to UK) and one service tunnel. All three tunnels were drilled below the seabed and link Folkestone in Kent to Coquelles in Pas-de-Calais.
However, the idea of connecting the UK and France by tunnel is much older than people think – dating back to the early 1800s when its supporters included Napoleon Bonaparte.
Work on experimental tunnels started back in 1880 at Abbot’s Cliff near Folkestone, Kent. Many of the workers used hand tools, but a state-of-the-art boring machine was also used. Work was eventually abandoned until construction on the tunnel as we now know it began again in 1988.
Frequently Asked Questions:
Thinking of hopping on Eurostar for your next European adventure? Got a couple of need-to-know questions before you book your trip? Here we’ve answered a selection of the most frequently asked questions from our customers.
Who can travel through the Channel Tunnel?
Foot passengers can travel with Eurostar, between our UK stations London St Pancras International and our stations on the continent . People who want to travel with their own vehicle or on a coach can use the Eurotunnel Le Shuttle between Folkestone and Calais. Before travelling with either Eurostar or Eurotunnel you will need to go through security, border and ticket checks before going through the Tunnel.
How much did it cost to build the Channel Tunnel?
It took just under six years and 13,000 workers to build the Channel Tunnel. The total cost came at an eye-watering £4.65 billion which would be the equivalent of £12 billion in today's money.
Why travel with Eurostar rather than drive?
* Avoid the stress of driving, with direct high-speed journeys to top destinations, from city centre to city centre.
* Great value fares with no additional costs like fuel, road tolls and parking.
* Simple connections with other rail services in Europe, allowing you to go beyond our direct destinations on a single booking.
* Travel in style on our comfortable trains, including our new, state-of-the art trains with wi-fi.
How fast does the Eurostar go?
The Eurostar travels through the Channel Tunnel at a speed of 100 miles per hour (160kph) although when the train is outside the tunnel it reaches speed of 186 miles per hour (300 kph).
Additional Information
Channel Tunnel, rail tunnel between England and France that runs beneath the English Channel. The Channel Tunnel, 50 km (31 miles) long, consists of three tunnels: two for rail traffic and a central tunnel for services and security. The tunnel runs between Folkestone, England, and Sangatte (near Calais), France, and is used for both freight and passenger traffic. Passengers can travel either by ordinary rail coach or within their own motor vehicles, which are loaded onto special railcars. Trains can travel through the tunnel at speeds as high as 160 km (100 miles) per hour; the trip takes about 35 minutes. It has the longest undersea portion of any tunnel in the world (37.8 km [23.5 miles]).
The often-considered idea of constructing a tunnel under the English Channel was revived in 1986 by the United Kingdom and France. A rail tunnel was chosen over proposals for a very long suspension bridge, a bridge-and-tunnel link, and a combined rail-and-road link, and the project was privately financed by a consortium of British and French corporations and banks; the Anglo-French company operating the tunnel is called Eurotunnel. Digging began on both sides of the Strait of Dover in 1987–88 and was completed in 1991. The tunnel was officially opened on May 6, 1994.
In 2007 the Channel Tunnel Rail Link (CTRL), also called High Speed 1, was opened to connect the Channel Tunnel with London, facilitating even greater movement of international passenger traffic between mainland Europe and the United Kingdom. The high-speed railway runs 108 km (67 miles) and crosses under the Thames. Its trains can reach speeds of up to 300 km (186 miles) per hour.
In June–July 2015 the problem of migrants—many of them from eastern Africa—sneaking aboard vehicles on trains in an attempt to immigrate to the United Kingdom reached crisis proportions. During that period at least nine individuals were killed while trying to make their way to England via the tunnel. The United Kingdom and France stepped up security measures to try to deter migrants from attempting the crossing.

#13 Science HQ » Gilbert's Syndrome » 2026-01-24 17:55:45
- Jai Ganesh
- Replies: 0
Gilbert's Syndrome
Gist
Gilbert syndrome is caused by a modified gene someone inherits from their parents. This gene usually controls an enzyme that helps break down bilirubin in the liver. When someone has this ineffective gene, their blood contains too much bilirubin. This is because the body isn't producing enough of the enzyme.
Gilbert Syndrome diagnosis involves blood tests showing elevated unconjugated bilirubin with normal liver function tests (LFTs) and a complete blood count (CBC) to rule out other liver or blood conditions, often discovered incidentally in teens/young adults experiencing mild jaundice. Genetic testing for the UGT1A1 gene mutation can confirm it, but isn't always necessary, as the pattern of normal liver function with elevated bilirubin is usually sufficient for a confirmed diagnosis.
Summary
Gilbert's syndrome (GS) is a syndrome in which the liver of affected individuals processes bilirubin more slowly than the majority, resulting in higher levels in the blood. Many people never have symptoms. Occasionally jaundice (a yellowing of the skin or whites of the eyes) may occur.
Gilbert syndrome is due to a genetic variant in the UGT1A1 gene, which results in decreased activity of the bilirubin uridine diphosphate glucuronosyltransferase enzyme. It is typically inherited in an autosomal recessive pattern and occasionally in an autosomal dominant pattern depending on the type of variant. Episodes of jaundice may be triggered by stress such as exercise, menstruation, or not eating. Diagnosis is based on elevated levels of unconjugated bilirubin in the blood without signs of liver problems or red blood cell breakdown.
Typically, no treatment is needed. Phenobarbital aids in the conjugation of bilirubin and can be prescribed if jaundice becomes significant. Gilbert syndrome is associated with decreased cardiovascular health risks but increased risks of some cancers and gallstones. Gilbert syndrome affects about 5% of people in the United States. Males are more often diagnosed than females. It is often not noticed until late childhood to early adulthood. The condition was first described in 1901 by Augustin Nicolas Gilbert.
Details
People with Gilbert's syndrome inherit a mutated gene that affects the liver’s ability to process bilirubin, a waste product that forms during the breakdown of old red blood cells. Jaundice (yellowish skin and eyes) occurs when too much bilirubin builds up in blood. Because this liver disease doesn’t cause serious problems, treatment isn’t necessary.
Overview:
What is Gilbert's syndrome?
Gilbert's syndrome is an inherited (genetic) liver disorder that affects the body’s ability to process bilirubin. Bilirubin is yellow liquid waste that occurs naturally as the body breaks down old red blood cells.
People with Gilbert's syndrome don’t produce enough liver enzymes to keep bilirubin at a normal level. As a result, excess bilirubin builds up in the body. Excess bilirubin is known as hyperbilirubinemia.
What is bilirubin?
Bilirubin is found in bile, a digestive liquid produced by the liver that helps the body absorb fat. Your liver is part of the digestive system. It filters toxins from blood, digests fats and stores glucose (a blood sugar) as glycogen to use for energy.
How common is Gilbert's syndrome?
An estimated 3% to 7% of Americans have Gilbert's syndrome. This type of liver disease is more common in males than in females. It affects all ages, races and ethnicities.
Who might have Gilbert's syndrome?
Gilbert's syndrome is genetic, meaning it’s passed down from parent to child through a change, or mutation, in a gene. People with Gilbert's syndrome inherit a mutated UGT1A1 gene.
Symptoms and Causes:
What causes Gilbert's syndrome?
A healthy UGT1A1 gene makes liver enzymes that break down bilirubin and remove it from the body. People with a mutated UGT1A1 gene only make about 30% of the enzymes they need. As a result, bilirubin doesn’t move into bile the way it should. The excess bilirubin builds up in blood.
What are the symptoms of Gilbert's syndrome?
Approximately 1 in 3 people with Gilbert's syndrome don’t have symptoms. They learn that they have the disease after getting blood tests to check for a different problem.
Among those with symptoms, the most common sign is jaundice, brought on by elevated levels of bilirubin in blood. Jaundice can turn your skin and whites of the eyes yellow, but it isn’t harmful.
Occasionally, people who have jaundice or Gilbert's syndrome also experience:
* Dark-colored urine or clay-colored stool.
* Difficulty concentrating.
* Dizziness.
* Gastrointestinal problems, such as abdominal pain, diarrhea and nausea.
* Fatigue.
* Flu-like symptoms, including fever and chills.
* Loss of appetite.
What worsens symptoms of Gilbert's syndrome?
These things can raise bilirubin levels in people with Gilbert's syndrome, leading to jaundice:
* Dehydration.
* Fasting or skipping meals.
* Illness or infections.
* Menstruation.
* Overexertion (too much physical activity).
* Stress.
Diagnosis and Tests:
How is Gilbert's syndrome diagnosed?
As a genetic condition, Gilbert's syndrome is present at birth. It often remains undiagnosed until blood tests detect high bilirubin levels. Diagnosis most commonly occurs when people are in their teens or early adulthood and getting blood tests for something else.
In addition to blood tests, you may get:
* Liver function tests to assess how well your liver is working and measure bilirubin levels.
* Genetic tests to check for the gene mutation that causes Gilbert's syndrome.
Management and Treatment:
What are the complications of Gilbert's syndrome?
Gilbert's syndrome is a mild condition. It doesn’t cause long-term complications or serious health problems.
How is Gilbert's syndrome managed or treated?
Jaundice can cause a yellowish appearance that may be unsettling. However, jaundice and Gilbert's syndrome don’t require treatment.
Additional Information:
Overview
Gilbert syndrome is a harmless liver condition in which the liver doesn't properly process bilirubin. Bilirubin is a substance produced by the breakdown of red blood cells.
Gilbert syndrome is a genetic condition passed down from your parents. You might not know you have Gilbert syndrome until it's discovered by accident, such as when a blood test shows raised bilirubin levels.
Gilbert syndrome needs no treatment.
The liver
The liver is your largest internal organ. About the size of a football, it's located mainly in the upper right portion of your abdomen — beneath the diaphragm and above your stomach. A small portion extends into the upper left quadrant.
Symptoms
The most common sign of Gilbert syndrome is an occasional yellowish tinge of the skin and the whites of the eyes, called jaundice. Jaundice is a result of slightly higher levels of bilirubin in the blood.
In people with Gilbert syndrome, bilirubin levels may increase due to:
* Illness, such as a cold or the flu.
* Fasting or eating a very low-calorie diet.
* Dehydration.
* Menstruation.
* Strenuous exercise.
* Stress.
When to see a doctor
Make an appointment with a healthcare professional if you have jaundice, which has many possible causes.
Causes
Gilbert syndrome is caused by a modified gene someone inherits from their parents. This gene usually controls an enzyme that helps break down bilirubin in the liver. When someone has this ineffective gene, their blood contains too much bilirubin. This is because the body isn't producing enough of the enzyme.
How the body processes bilirubin
Bilirubin is a yellowish pigment made when the body breaks down old red blood cells. Bilirubin travels through the bloodstream to the liver, where the enzyme breaks down the pigment and removes it from the bloodstream.
The bilirubin passes from the liver into the intestines with bile. It's then excreted in stool. A small amount of bilirubin remains in the blood.
How the modified gene is passed through families
The modified gene that causes Gilbert syndrome is common. Many people carry one copy of this gene. In most cases, two modified copies are needed to cause Gilbert syndrome.
Risk factors
Although it's present from birth, Gilbert syndrome usually isn't noticed until puberty or later. This is because bilirubin production increases during puberty. Risk factors for Gilbert syndrome include:
* Both parents carry the modified gene that causes the disorder.
* Being male.
Complications
The low level of the bilirubin-processing enzyme that causes Gilbert syndrome also may increase the side effects of certain medicines, since this enzyme plays a role in helping clear these medicines from the body.
These medicines include:
* Irinotecan (Camptosar), a cancer chemotherapy drug.
* Some protease inhibitors used to treat HIV.
If you have Gilbert syndrome, talk to a healthcare professional before taking new medicines. Also, having any other condition that affects the destruction of red blood cells may increase the risk of developing gallstones.

#14 This is Cool » Smartphone » 2026-01-24 16:05:10
- Jai Ganesh
- Replies: 0
Smartphone
Gist
A cellphone is a mobile device for calls and texts, while a smartphone is a type of cellphone with advanced computing, internet, and app capabilities, essentially blending a phone with a handheld computer. All smartphones are cellphones, but basic cellphones (also called feature phones) lack the sophisticated operating systems, app stores, and features like GPS, email, and advanced cameras found on smartphones.
Smartphones offer a range of different benefits such as increased portability, improved user experience and accessibility compared to traditional computers. With smartphones users have instantaneous access to important documents, emails and applications which allows them to work more efficiently on the go.
Summary
A smartphone is a mobile device that combines the functionality of a traditional mobile phone with advanced computing capabilities. It typically has a touchscreen interface, allowing users to access a wide range of applications and services, such as web browsing, email, and social media, as well as multimedia playback and streaming. Smartphones have built-in cameras, GPS navigation, and support for various communication methods, including voice calls, text messaging, and internet-based messaging apps. Smartphones are distinguished from older-design feature phones by their more advanced hardware capabilities and extensive mobile operating systems, access to the internet, business applications, mobile payments, and multimedia functionality, including music, video, gaming, radio, and television.
Smartphones typically feature metal–oxide–semiconductor (MOS) integrated circuit (IC) chips, various sensors, and support for multiple wireless communication protocols. Examples of smartphone sensors include accelerometers, barometers, gyroscopes, and magnetometers; they can be used by both pre-installed and third-party software to enhance functionality. Wireless communication standards supported by smartphones include LTE, 5G NR, Wi-Fi, Bluetooth, and satellite navigation. By the mid-2020s, manufacturers began integrating satellite messaging and emergency services, expanding their utility in remote areas without reliable cellular coverage. Smartphones have largely replaced personal digital assistant (PDA) devices, handheld/palm-sized PCs, portable media players (PMP), point-and-shoot cameras, camcorders, and, to a lesser extent, handheld video game consoles, e-reader devices, pocket calculators, and GPS tracking units.
Following the rising popularity of the iPhone in the late 2000s, the majority of smartphones have featured thin, slate-like form factors with large, capacitive touch screens with support for multi-touch gestures rather than physical keyboards. Most modern smartphones have the ability for users to download or purchase additional applications from a centralized app store. They often have support for cloud storage and cloud synchronization, and virtual assistants. Since the early 2010s, improved hardware and faster wireless communication have bolstered the growth of the smartphone industry. As of 2014, over a billion smartphones are sold globally every year. In 2019 alone, 1.54 billion smartphone units were shipped worldwide. As of 2020, 75.05 percent of the world population were smartphone users.
Details
Isn’t it great when science fiction becomes science fact? If you’re a little older, you probably wanted a communication device just like the one Captain Kirk used in the TV series “Star Trek” when you were growing up. Kirk and the crew of the USS Enterprise could talk over vast distances with these personal communication devices. Without the “communicator, the order to “beam us up, Mr. Scott” would have fallen on deaf ears, and we all know what would have happened to Kirk if he didn’t have any bars on his device.
Now that we’re well into the 21st century, our “communicators” make the ones on “Star Trek” seem like antiques. Not only can we talk to one another on our smartphones, but we can text, play music or a game, get directions, take pictures, check e-mail, find a great restaurant, surf the Internet, watch a movie. You get the idea. Smartphones are cell phones on steroids. Why is that?
Unlike traditional cell phones, smartphones, with their big old memories, allow individual users like you and me to install, configure and run applications, or apps, of our choosing. A smartphone offers the ability to configure the device to your particular way of doing things. The software in the old-style flip phones offers only limited choices for reconfiguration, forcing you to adapt to the way they are set up. On a standard phone, whether or not you like the built-in calendar application, you’re stuck with it except for a few minor tweaks. But if that phone were a smartphone, you could install any compatible calendar application you liked.
Here's a list of some of the additional capabilities smartphones have, from intuitive to perhaps less so:
* Manage your personal info including notes, calendar and to-do lists
* Communicate with laptop or desktop computers
* Sync data with applications like Microsoft Outlook and Apple's iCal calendar programs
* Host applications such as word processing programs or video games
* Scan a receipt
* Cash a check
* Replace your wallet. A smartphone can store credit card information and discount or membership card info
* Pay bills by downloading apps such as PayPal and CardStar
* Allow you to create a WiFi network that multiple devices can use simultaneously. That means you can access the Internet from your iPad or laptop without a router or another peripheral device.
Work:
The Layers of a Smartphone
Everyone has a smartphone, or so it seems. In fact, there were an estimated 1.4 billion smartphones in the world as of December 2013. People are constantly talking on them, taking pictures, surfing the Internet and doing dozens of other things, including shopping for cars. Captain Kirk would be jealous.
At their core, smartphones, and all cell phones for that matter, are mini radios, sending and receiving radio signals. Cell phone networks are divided into specific areas called cells. Each cell has an antenna that receives cell phone signals. The antenna transmits signals just like a radio station, and your phone picks up those signals just as a radio does.
Smartphones use cell phone network technology to send and receive data (think phone calls, Web browsing, file transfers). Developers classify this technology into generations. Do you remember the first generation? It included analog cell phone technology. However, as cell phone technology progressed, the protocols became more advanced. In 2014, cell phones are in the world of the fourth generation, or 4G. Although most carriers are expanding their 4G technology, some companies, such as Samsung, are developing 5G technology, which if recent tests are any indication, will allow you to download an entire movie in less than a second. You can read more about network technologies and protocols in the article How Cell Phones Work.
Smartphone Hardware and Software
Smartphone Hardware and Software
As long as we're talking details, let's have a quick look at smartphone hardware.
Some smartphones run on processors. Along with processors, smartphones also have computer chips that provide functionality. Phones with cameras have high-resolution image sensors, just like digital cameras. Other chips support complex functions such as browsing the Internet, sharing multimedia files or playing music without placing too great a demand on the phone’s battery. Some manufacturers develop chips that integrate multiple functions to help reduce the overall cost (fewer chips produced per phone help offset production costs).
You can visualize software for smartphones as a software stack. The stack consists of the following layers:
kernel -- management systems for processes and drivers for hardware
middleware -- software libraries that enable smartphone applications (such as security, Web browsing and messaging)
application execution environment (AEE) -- application programming interfaces, which allow developers to create their own programs
user interface framework -- the graphics and layouts seen on the screen
application suite -- the basic applications users access regularly such as menu screens, calendars and message inboxes
Smartphone Operating Systems
The most important software in any smartphone is its operating system (OS). An operating system manages the hardware and software resources of smartphones. Some platforms cover the entire range of the software stack. Others may only include the lower levels (typically the kernel and middleware layers) and rely on additional software platforms to provide a user interface framework. We've added some snapshots of specific smartphone operating systems.
Designed primarily for touch-screen mobile devices, Android, or Droid, technology is the operating system that most mobile telephones used as of Comscore's February 2014 numbers. Developed by Google, most people consider the Droid technology revolutionary because its open source technology allows people to write program codes and applications for the operating system, which means Android is evolving constantly. Smartphone users can decide whether to download the applications. Moreover, Android operating systems can run multiple applications, allowing users to be multitasking mavens. And get this: Any hardware manufacturer is free to produce its own Android phone by using the operating system. In fact, many smartphone companies do just that. Android app’s store has hundreds of thousands of apps.
Apple is always innovating, and iOS allows iPhone screens to be used simply and logically. Touted by Apple as the “world’s most advance mobile operating system,” iOS supports more access from sports scores to restaurant recommendations. As of publication, its latest version iOS7 allows for automatic updates and a control center that gives users access to their most used features. It also makes surfing the net easier with an overhaul to the Safari browser.
Reviewers say that Windows Phone 8 (WP8) is as simple to use as iOS and as easy to customize as Android. Its crowning achievement is LiveTiles, which are programmed squares that users can rearrange on their screen to easily access the information they want. WP8 works well with other Microsoft products, including Office and Exchange. For those who do a lot of calling, connecting to Facebook and texting, WP8 may meet their needs.
At first glance, experts say, Ubuntu 13.10 Touch might seem like an ordinary operating system, but it’s not. Experts say Ubuntu Touch one of the easiest systems to use, allowing seamless navigation with multiple scopes. There are no hardware buttons on the bottom, for example. Instead, Ubuntu works from the edges. Developed by Canonical, the Ubuntu Touch allows users to unlock the phone from the right edge. You can swipe down from the top edge to access the phone’s indicators, including date, time, messages (from variety of sources, ie: Skype and Facebook) and wireless networks. The phone also makes it easy for people to organize and share photos. Every shot is automatically uploaded to a personal cloud account, which makes it available on all devices, including iOS, Android and Windows.
Flexible Interfaces
The core services on smartphones all tie in to the idea of a multipurpose device that can effectively multitask. A user can watch a video, field a phone call, then return to the video after the call, all without closing each application. Or he or she can flip through the digital calendar and to-do list applications without interrupting the voice call. All of the data stored on the phone can be synchronized with outside applications or manipulated by third-party phone applications in numerous ways. Here are a few systems that smartphones support.
Bluetooth
This short-range radio service allows phones to wirelessly link up with each other and with other nearby devices that support it. Examples include printers, scanners, input devices, computers and headsets.
Some varieties of Bluetooth only allow communication with one device at a time, but others allow simultaneous connection with multiple devices. To learn more, check out How Bluetooth Works.
Data Synchronization
A phone that keeps track of your personal information, like appointments, to-do lists, addresses, and phone numbers, needs to be able to communicate with all of the other devices you use to keep track of those things. There are hundreds of possible platforms and applications you might use for this in the course of a day. If you want to keep all of this data synchronized with what's on your phone, then you generally have to look for a cell phone that speaks the languages of all of the devices and applications you use. Or you can go out and buy new applications that speak the language of your cell phone.
The Open Mobile Alliance (OMA) is a collaborative organization with the following mission:
* Be the center of mobile service enabler specification work, helping the creation of interoperable services across countries, operators and mobile terminals that will meet the needs of the user.
The OMA formed a Data Synchronization Working Group, which continued the work begun by the SyncML Initiative. SyncML was an open-standards project designed to eliminate the trouble of worrying about whether your personal information manager tools sync up with your phone and vice versa. The project is designed so that any kind of data can be synchronized with any application on any piece of hardware, through any network, provided that they are all programmed to OMA standards. This includes synchronization over the Web, Bluetooth, mail protocols and TCP/IP networks.
SyncML allows data to be synchronized from a phone to Windows, Mac and Linux applications using Bluetooth, infrared, HTTP or a USB cable. Visit the OMA Web site for more information.
Java
A smartphone that's compatible with the Java programming language allows the user to load and run Java applications and MIDlets. MIDlets are applications that use a subset of Java and are specifically programmed to run on wireless devices. Java MIDlets include add-ons, games, applications and utilities.
Since there are millions of Java developers worldwide, and the Java development tools are freely accessible, smartphone users can install thousands of third-party applications on their phones. Because of the way the OS architecture of most phones is built, these applications can access and use all of the data on the user's phone.
The Future of Smartphones
With data transmission rates reaching blistering speeds and the incorporation of WiFi technology, the sky is the limit on what smartphones can do. Possibly the most exciting thing about smartphone technology is that the field is still wide open. It's an idea that probably hasn't found its perfect, real-world implementation yet. Every crop of phones brings new designs and new interface ideas. No one developer or manufacturer has come up with the perfect shape, size or input method yet. The next "killer app" smartphone could look like a flip phone, a tablet PC, a candy bar or something no one has conceived of yet.
Perhaps the most challenging consideration for the future is security. Smartphones may be vulnerable to security breaches such as an Evil Twin attack. In one of these attacks, a hacker sets a server’s service identifier to that of a legitimate hotspot or network while simultaneously blocking traffic to the real server. When a user connects with the hacker’s server, information can be intercepted and security is compromised.
On the other side, some critics argue that anti-virus software manufacturers greatly exaggerate the risks, harms and scope of phone viruses in order to help sell their software. Read more in the article How Cell Phone Viruses Work.
The incredible diversity in smartphone hardware, software and network protocols inhibit practical, broad security measures. Most security considerations either focus on particular operating systems or have more to do with user behavior than network security.
Additional Information
A smartphone is a mobile telephone with a display screen (typically a liquid crystal display, or LCD), built-in personal information management programs (such as an electronic calendar and address book)), and an operating system (OS) that allows other computer software to be installed for Web browsing, email, music, video, and other applications. A smartphone may be thought of as a handheld computer integrated within a mobile telephone.
The first smartphone was designed by IBM and sold by BellSouth (formerly part of the AT&T Corporation) in 1993. It included a touchscreen interface for accessing its calendar, address book, calculator, and other functions. As the market matured and solid-state computer memory and integrated circuits became less expensive over the following decade, smartphones became more computer-like, and more advanced services, such as Internet access, became possible. Advanced services became ubiquitous with the introduction of the so-called third-generation (3G) mobile phone networks in 2001. Before 3G, most mobile phones could send and receive data at a rate sufficient for telephone calls and text messages. Using 3G, communication takes place at bit-rates high enough for sending and receiving photographs, video clips, music files, e-mails, and more. Most smartphone manufacturers license an operating system, such as Microsoft Corporation’s Windows Mobile OS, Symbian OS, Google’s Android OS, or Palm OS. Research in Motion’s BlackBerry and Apple Inc.’s iPhone have their own proprietary systems.
Smartphones contain either a keyboard integrated with the telephone number pad or a standard “QWERTY” keyboard for text messaging, e-mailing, and using Web browsers. “Virtual” keyboards can be integrated into a touch-screen design. Smartphones often have a built-in camera for recording and transmitting photographs and short videos. In addition, many smartphones can access Wi-Fi “hot spots” so that users can access VoIP (voice over Internet protocol) rather than pay cellular telephone transmission fees. The growing capabilities of handheld devices and transmission protocols have enabled a growing number of inventive and fanciful applications—for instance, “augmented reality,” in which a smartphone’s global positioning system (GPS) location chip can be used to overlay the phone’s camera view of a street scene with local tidbits of information, such as the identity of stores, points of interest, or real estate listings.
4G
4G (Fourth Generation) is a mobile network technology offering significantly faster data speeds than 3G, enabling HD streaming, faster browsing, and lower latency. It primarily uses 4G LTE (Long Term Evolution) to provide speeds, often up to 100 Mbps, and is designed for all-IP, packet-switched communication, including voice-over-LTE (VoLTE).
4G refers to the fourth generation of cellular network technology, introduced in the late 2000s and early 2010s. Compared to preceding third-generation (3G) technologies, 4G has been designed to support all-IP communications and broadband services, and eliminates circuit switching in voice telephony.[1] It also has considerably higher data bandwidth compared to 3G, enabling a variety of data-intensive applications such as high-definition media streaming and the expansion of Internet of Things (IoT) applications.
The earliest deployed technologies marketed as "4G" were Long Term Evolution (LTE), developed by the 3GPP group, and Mobile Worldwide Interoperability for Microwave Access (Mobile WiMAX), based on IEEE specifications. These provided significant enhancements over previous 3G and 2G.
Technical overview
In November 2008, the International Telecommunication Union-Radio communications sector (ITU-R) specified a set of requirements for 4G standards, named the International Mobile Telecommunications Advanced (IMT-Advanced) specification, setting peak speed requirements for 4G service at 100 megabits per second (Mbit/s)(=12.5 megabytes per second) for high mobility communication (such as from trains and cars) and 1 gigabit per second (Gbit/s) for low mobility communication (such as pedestrians and stationary users).[5]
Since the first-release versions of Mobile WiMAX and LTE support much less than 1 Gbit/s peak bit rate, they are not fully IMT-Advanced compliant, but are often branded 4G by service providers. According to operators, a generation of the network refers to the deployment of a new non-backward-compatible technology. On December 6, 2010, ITU-R recognized that these two technologies, as well as other beyond-3G technologies that do not fulfill the IMT-Advanced requirements, could nevertheless be considered "4G", provided they represent forerunners to IMT-Advanced compliant versions and "a substantial level of improvement in performance and capabilities with respect to the initial third generation systems now deployed". Both the original LTE and WiMAX standards had previously sometimes been referred to as 3.9G/3.95G. The ITU's new definition for 4G also included Evolved High Speed Packet Access (HSPA+).
Mobile WiMAX Release 2 (also known as WirelessMAN-Advanced or IEEE 802.16m) and LTE Advanced (LTE-A) are IMT-Advanced compliant backwards compatible versions of the above two systems, standardized during the spring 2011, and promising speeds in the order of 1 Gbit/s. In January 2012, the ITU backtracked on its previous definition for 4G, claiming that Mobile WiMAX 2 and LTE Advanced are "true 4G" while their predecessors are "transitional" 3G-4G.
As opposed to earlier generations, a 4G system does not support traditional circuit-switched telephony service, but instead relies on all-Internet Protocol (IP) based communication such as IP telephony. As seen below, the spread spectrum radio technology used in 3G systems is abandoned in all 4G candidate systems and replaced by OFDMA multi-carrier transmission and other frequency-domain equalization (FDE) schemes, making it possible to transfer very high bit rates despite extensive multi-path radio propagation (echoes). The peak bit rate is further improved by smart antenna arrays for multiple-input multiple-output (MIMO) communications.
5G
5G, fifth-generation telecommunications technology. Introduced in 2019 and now globally deployed, 5G delivers faster connectivity with higher bandwidth and “lower latency” (shorter delay times), improving the performance of phone calls, streaming, videoconferencing, gaming, and business applications as well as the responsiveness of connected systems and mobile apps. 5G can double the download speeds for smartphones and improve performance considerably more for devices tied to the Internet of Things (IoT).
5G technology improves the data processing of more-advanced digital operations such as those tied to machine learning (ML), artificial intelligence (AI), virtual reality (VR), and augmented reality (AR), improving performance and the user experience alike. It also better supports autonomous vehicles, drones, and other robotic systems.
How 5G works
5G signals rely on a different part of the radiofrequency spectrum than previous versions of cellular technology. As a result, mobile phones and other devices must be built with a specific 5G microchip.
Three primary types of 5G technology exist: low-band networks that support a wide coverage area but increase speeds only by about 20 percent over 4G; high-band networks that deliver ultrafast connectivity but which are limited by distance and access to 5G base stations (which transmit the signals for the technology); and mid-band networks that balance both speed and breadth of coverage. 5G also supports “OpenRoaming” capabilities that allow a user to switch seamlessly and automatically from a cellular to a Wi-Fi connection while traveling, eliminating any interruption of service and the need for entering passwords to access the latter.
Telecom providers use a different type of antenna, known as MIMO (multiple-input multiple-output), to transmit 5G signals. This does not require the traditional large cell tower (base station) but can be deployed through a multiplicity of “small cells” (which are the micro boxes commonly seen on poles and lamp posts). Many observers see this as an aesthetic improvement to the city landscape. Proximity to these cells remains an issue globally, however, especially for rural and remote regions, underscoring the current limitations of 5G.
Security concerns accompany changing technologies. Since 5G networks rely on cloud-based data storage, they are susceptible to the same possible dangers as other types of cellar and noncellular networks, including data damage, cyberattacks, and theft. Additionally, companies must be mindful of data-point vulnerabilities during a transition to 5G from networks with different security capabilities.

#15 Science HQ » Mandible » 2026-01-24 01:09:38
- Jai Ganesh
- Replies: 0
Mandible
Gist
In jawed vertebrates, the mandible (from the Latin mandibula, 'for chewing'), lower jaw, or jawbone is a bone that makes up the lower – and typically more mobile – component of the mouth (the upper jaw being known as the maxilla).
Upper jaw (maxilla): Fixed bone that holds your upper teeth and shapes your face. Lower jaw (mandible): The only movable bone in your skull and the strongest facial bone.
The mandible is the largest, strongest, and only movable bone in the human skull, forming the lower jaw, holding the lower teeth, and enabling mastication and speech. It is a U-shaped bone consisting of a horizontal body and two vertical rami that articulate with the temporal bone. It fuses into one bone in early life.
Summary
In jawed vertebrates, the mandible (from the Latin mandibula, 'for chewing'), lower jaw, or jawbone is a bone that makes up the lower – and typically more mobile – component of the mouth (the upper jaw being known as the maxilla).
The jawbone is the skull's only movable, posable bone, sharing joints with the cranium's temporal bones. The mandible hosts the lower teeth (their depth delineated by the alveolar process). Many muscles attach to the bone, which also hosts nerves (some connecting to the teeth) and blood vessels. Amongst other functions, the jawbone is essential for chewing food.
Owing to the Neolithic advent of agriculture (c. 10,000 BCE), human jaws evolved to be smaller. Although it is the strongest bone of the facial skeleton, the mandible tends to deform in old age; it is also subject to fracturing. Surgery allows for the removal of jawbone fragments (or its entirety) as well as regenerative methods. Additionally, the bone is of great forensic significance.
Details:
Introduction
The mandible is the largest and strongest bone of the human skull. It is commonly known as the lower jaw and is located inferior to the maxilla. It is composed of a horseshoe-shaped body which lodges the teeth, and a pair of rami which projects upwards to form a temporomandibular joint.
Structure
The mandible is formed by a body and a pair of rami along with condyloid and coronoid processes.
Body
Body is the anterior portion of the mandible. Body has two surfaces: outer and inner and two borders: upper and lower border. The body ends and the rami begin on either side at the angle of the mandible, also known as the gonial angle.
1. Outer surface is also known as external surface and has following characteristics:
* Mandibular symphysis/ Symphysis menti at midline which joins left and right half of the bone, detected as a subtle ridge in the adult.
* The inferior portion of the ridge divides and encloses a midline depression called the mental protuberance, also known as chin. The edges of the mental protuberance are elevated, forming the mental tubercle.
* Laterally to the ridge and below the incisive teeth is a depression known as the incisive fossa.
* Below the second premolar is the mental foramen, in which the mental nerve and vessels exit.
* The oblique line courses posteriorly from the mental tubercle to the anterior border of the ramus.
2. Inner surface is also known as internal surface and has following features:
* The mylohyoid line is a prominent ridge that runs obliquely downwards and forwards from below the third molar tooth to the median area below the genial tubercles.
* Below the mylohyoid line, the surface is slightly hollowed out to form the sub-mandibular fossa, which lodges the submandibular gland.
* Above the mylohyoid line, there is the sublingual fossa in which the sublingual gland lies.
* The posterior surface of the symphysis menti is marked by four small elevations called the superior and inferior genial tubercles.
3. Upper border (Alveolar border)
It consist of sockets for the teeth.
4. Lower border (Inferior border)
It is also known as base. There is a fossa present at the side of midline known as digastric fossa.
Ramus
The ramus is lateral continuation of the body and is quadrilateral in shape. The coronoid process is the anterosuperior projection of the ramus which is triangular in shape. Whereas posterosuperior projection of ramus is known as condyloid process whose head is covered with fibrocartilage and form a temporomandibular joint. The constricted part below condyloid process is neck. Condyloid and coronoid process are separated by a mandibular notch. It has two surfaces: medial and lateral and four borders: superior, inferior, anterior and posterior.
Ossification
Mandible is the second bone to ossify after clavicle. Each half of the mandible ossifies from only one centre at the sixth week of intrauterine life in the mesenchymal sheath of Meckel's cartilage near the future mental foramen. The first pharyngeal arch, known as the mandibular arch, gives rise to the Meckel cartilage. A fibrous membrane covers the left and right Meckel cartilage at their ventral ends. These two halves eventually fuse via fibrocartilage at the mandibular symphysis. Thus, at birth, the mandible is still composed of two separate bones. Ossification and fusion of the mandibular symphysis occur during the first year of life, resulting in a single bone. The remnant of the mandibular symphysis is a subtle ridge at the midline of the mandible.
The mandible changes throughout the life. In infant and children, the angle of mandible is obtuse with 140 degrees or more making head in line with the body of the mandible. Whereas in adult the angle decreases to about 110-120 degree making ramus almost vertical.
Additional Information
Mandible, in anatomy, is the movable lower jaw, consisting of a single bone or of completely fused bones in humans and other mammals. In birds, the mandible constitutes either the upper or the lower segment of the bill, and in invertebrates it is any of the various mouthparts that holds or bites food materials, including either of the paired mouth appendages of an arthropod that form the biting jaws.
In humans, the mandible is the only mobile bone of the skull (other than the tiny bones of the middle ear). It is attached to muscles involved in chewing and other mouth movements and functions by moving in opposition to the maxilla (upper jaw); together, the two parts are used for biting, chewing, and handling food. The structure of the human mandible resembles a more or less horizontal arch, which holds the teeth and contains blood vessels and nerves. At the rear of the mandible, two more or less vertical portions (rami) form movable hinge joints, one on each side of the head, articulating with the glenoid cavity of the temporal bone of the skull to form the temporomandibular joints. The rami also provide attachment for muscles important in chewing. The centre front of the arch is thickened and buttressed to form the chin, a development unique to humans and some of their recent ancestors; the great apes and other animals lack chins. In the human fetus and infant, the maxilla and the mandible are each separated at the midline; the halves fuse a few months after birth.
Invertebrate jaw and mouthpart structures vary markedly. For example, in the primitive bloodsucking flies (e.g., the horse fly [Tabanus]), the mandibles and maxillae form serrated blades that cut through the skin and blood vessels of the host animal. In the mosquito (Culicidae), the mandibles and associated structures have become exceedingly slender stylets that form a fine bundle used for piercing skin and entering blood vessels. In the housefly (Musca domestica), the mandibles and maxillae have been lost; the tonguelike labium alone remains and serves for feeding on exposed surfaces. Among crustaceans, processes at the base of the antennae may help the mandibles push food into the mouth. The paired mandibles of a nauplius (the most widespread and typical crustacean larva to emerge from the egg) each have two branches, one with a chewing lobe and the other with a compressing lobe at the base; the mandibles may also be used for swimming. In the adult crustacean, each mandible loses one of the branches, sometimes retaining the other as a palp, and the base may develop into a powerful jaw. An alternative development is found in some of the blood-sucking parasites, in which the mandibles form needlelike stylets for piercing a host.
In humans, the most common conditions that affect the function of the mandible are temporomandibular joint disorders (TMDs), of which there are about 30 different types. TMDs may have an impact on the function of the jaw muscles and the temporomandibular joints and may irritate associated nerves. The cause of a TMD is often unclear; factors that may play a role include osteoarthritis and physical trauma. Symptoms vary but may include dizziness, earache, facial pain, headache, jaw tenderness, and reduced jaw mobility. Many TMDs resolve on their own; otherwise, treatment ranges from simple dietary changes (e.g., eating only soft foods) to physical therapy or medication to the use of intraoral appliances (devices fitted over the teeth) to complex surgical or dental procedures.

#16 Re: This is Cool » Miscellany » 2026-01-22 22:59:01
2477) Photosysthesis
Gist
Photosynthesis is the vital process where plants, algae, and some bacteria use sunlight, water, and carbon dioxide to create their own food (glucose/sugars) and release oxygen, converting light energy into stored chemical energy, forming the base of most food webs and producing atmospheric oxygen. It involves light-dependent reactions (capturing energy in ATP/NADPH using chlorophyll) and light-independent reactions (Calvin Cycle) that use this energy to build sugars, occurring in chloroplasts.
Photosynthesis is the process where plants, algae, and some bacteria use sunlight, water, and carbon dioxide to create their own food (glucose/sugar) and release oxygen as a byproduct, converting light energy into stored chemical energy. This vital process, primarily occurring in chloroplasts, provides the energy and oxygen necessary for most life on Earth.
Summary
Photosynthesis is a system of biological processes by which photopigment-bearing autotrophic organisms, such as most plants, algae and cyanobacteria, convert light energy — typically from sunlight — into the chemical energy necessary to fuel their metabolism. The term photosynthesis usually refers to oxygenic photosynthesis, a process that releases oxygen as a byproduct of water splitting. Photosynthetic organisms store the converted chemical energy within the bonds of intracellular organic compounds (complex compounds containing carbon), typically carbohydrates like sugars (mainly glucose, fructose and sucrose), starches, phytoglycogen and cellulose. When needing to use this stored energy, an organism's cells then metabolize the organic compounds through cellular respiration. Photosynthesis plays a critical role in producing and maintaining the oxygen content of the Earth's atmosphere, and it supplies most of the biological energy necessary for complex life on Earth.
Some organisms also perform anoxygenic photosynthesis, which does not produce oxygen. Some bacteria (e.g. purple bacteria) use bacteriochlorophyll to split hydrogen sulfide as a reductant instead of water, releasing sulfur instead of oxygen, which was a dominant form of photosynthesis in the euxinic Canfield oceans during the Boring Billion. Archaea such as Halobacterium also perform a type of non-carbon-fixing anoxygenic photosynthesis, where the simpler photopigment retinal and its microbial rhodopsin derivatives are used to absorb green light and produce a proton (hydron) gradient across the cell membrane, and the subsequent ion movement powers transmembrane proton pumps to directly synthesize adenosine triphosphate (ATP), the "energy currency" of cells. Such archaeal photosynthesis might have been the earliest form of photosynthesis that evolved on Earth, as far back as the Paleoarchean, preceding that of cyanobacteria (see Purple Earth hypothesis).
While the details may differ between species, the process always begins when light energy is absorbed by the reaction centers, proteins that contain photosynthetic pigments or chromophores. In plants, these pigments are chlorophylls (a porphyrin derivative that absorbs the red and blue spectra of light, thus reflecting green) held inside chloroplasts, abundant in leaf cells. In cyanobacteria, they are embedded in the plasma membrane. In these light-dependent reactions, some energy is used to strip electrons from suitable substances, such as water, producing oxygen gas. The hydrogen freed by the splitting of water is used in the creation of two important molecules that participate in energetic processes: reduced nicotinamide adenine dinucleotide phosphate (NADPH) and ATP.
In plants, algae, and cyanobacteria, sugars are synthesized by a subsequent sequence of light-independent reactions called the Calvin cycle. In this process, atmospheric carbon dioxide is incorporated into already existing organic compounds, such as ribulose bisphosphate (RuBP). Using the ATP and NADPH produced by the light-dependent reactions, the resulting compounds are then reduced and removed to form further carbohydrates, such as glucose. In other bacteria, different mechanisms like the reverse Krebs cycle are used to achieve the same end.
The first photosynthetic organisms probably evolved early in the evolutionary history of life using reducing agents such as hydrogen or hydrogen sulfide, rather than water, as sources of electrons. Cyanobacteria appeared later; the excess oxygen they produced contributed directly to the oxygenation of the Earth, which rendered the evolution of complex life possible. The average rate of energy captured by global photosynthesis is approximately 130 terawatts, which is about eight times the total power consumption of human civilization. Photosynthetic organisms also convert around 100–115 billion tons (91–104 Pg petagrams, or billions of metric tons), of carbon into biomass per year. Photosynthesis was discovered in 1779 by Jan Ingenhousz who showed that plants need light, not just soil and water.
Details
Photosynthesis is the process by which green plants and certain other organisms transform light energy into chemical energy. During photosynthesis in green plants, light energy is captured and used to convert water, carbon dioxide, and minerals into oxygen and energy-rich organic compounds.
Importance of photosynthesis
It would be impossible to overestimate the importance of photosynthesis in the maintenance of life on Earth. The Great Oxidation Event, which began about 2.4 billion years ago and was largely driven by the photosynthetic cyanobacteria, raised atmospheric oxygen to nearly 1 percent of present levels over a span of 600 million years, paving the way for the evolution of most forms of multicellular life. Photosynthesis completely transformed Earth’s environment and biosphere. The life-giving process continues to sustain biodiversity since autotrophs are foundational to nearly every food web on the planet. If photosynthesis ceased, there would soon be little food or other organic matter on Earth. Most organisms would disappear, and in time Earth’s atmosphere would become nearly devoid of gaseous oxygen. The only organisms able to exist under such conditions would be the chemosynthetic bacteria, which can utilize the chemical energy of certain inorganic compounds and thus are not dependent on the conversion of light energy.
Energy produced by photosynthesis carried out by plants millions of years ago is responsible for the fossil fuels (i.e., coal, oil, and natural gas) that power industrial society. In past ages, green plants and small organisms that fed on plants increased faster than they were consumed, and their remains were deposited in Earth’s crust by sedimentation and other geological processes. There, protected from oxidation, these organic remains were slowly converted to fossil fuels. These fuels not only provide much of the energy used in factories, homes, and transportation but also serve as the raw material for plastics and other synthetic products. Unfortunately, modern civilization is using up in a few centuries the excess of photosynthetic production accumulated over millions of years. Consequently, the carbon dioxide that has been removed from the air to make carbohydrates in photosynthesis over millions of years is being returned at an incredibly rapid rate. The carbon dioxide concentration in Earth’s atmosphere is rising the fastest it ever has in Earth’s history, and this phenomenon—known as global warming—is expected to have major implications on Earth’s climate.
Evolution of the process
Although life and the quality of the atmosphere today depend on photosynthesis, it is likely that green plants evolved long after the first living cells. When Earth was young, electrical storms and solar radiation probably provided the energy for the synthesis of complex molecules from abundant simpler ones, such as water, ammonia, and methane. The first living cells probably evolved from these complex molecules. For example, the accidental joining (condensation) of the amino acid glycine and the fatty acid acetate may have formed complex organic molecules known as porphyrins. These molecules, in turn, may have evolved further into colored molecules called pigments—e.g., chlorophylls of green plants, bacteriochlorophyll of photosynthetic bacteria, hemin (the red pigment of blood), and cytochromes, a group of pigment molecules essential in both photosynthesis and cellular respiration.
Primitive colored cells then had to evolve mechanisms for using the light energy absorbed by their pigments. At first, the energy may have been used immediately to initiate reactions useful to the cell. As the process for using light energy continued to evolve, however, a larger part of the absorbed light energy probably was stored as chemical energy, to be used to maintain life. Green plants, with their ability to use light energy to convert carbon dioxide and water to carbohydrates and oxygen, are the culmination of this evolutionary process.
The first oxygenic (oxygen-producing) cells probably were the cyanobacteria (blue-green algae), which appeared about two billion to three billion years ago. These microscopic organisms are believed to have greatly increased the oxygen content of the atmosphere, making possible the development of aerobic (oxygen-using) organisms. Cyanophytes are prokaryotic cells; that is, they contain no distinct membrane-enclosed subcellular particles (organelles), such as nuclei and chloroplasts. Green plants, by contrast, are composed of eukaryotic cells, in which the photosynthetic apparatus is contained within membrane-bound chloroplasts. The complete genome sequences of cyanobacteria and higher plants provide evidence that the first photosynthetic eukaryotes were likely the red algae that developed when nonphotosynthetic eukaryotic cells engulfed cyanobacteria. Within the host cells, these cyanobacteria evolved into chloroplasts.
There are a number of photosynthetic bacteria that are not oxygenic (e.g., the sulfur bacteria previously discussed). The evolutionary pathway that led to these bacteria diverged from the one that resulted in oxygenic organisms. In addition to the absence of oxygen production, nonoxygenic photosynthesis differs from oxygenic photosynthesis in two other ways: light of longer wavelengths is absorbed and used by pigments called bacteriochlorophylls, and reduced compounds other than water (such as hydrogen sulfide or organic molecules) provide the electrons needed for the reduction of carbon dioxide.
Additional Information
Photosynthesis is the process by which plants use sunlight, water, and carbon dioxide to create oxygen and energy in the form of sugar.
Most life on Earth depends on photosynthesis.The process is carried out by plants, algae, and some types of bacteria, which capture energy from sunlight to produce oxygen (O2) and chemical energy stored in glucose (a sugar). Herbivores then obtain this energy by eating plants, and carnivores obtain it by eating herbivores.
The process
During photosynthesis, plants take in carbon dioxide (CO2) and water (H2O) from the air and soil. Within the plant cell, the water is oxidized, meaning it loses electrons, while the carbon dioxide is reduced, meaning it gains electrons. This transforms the water into oxygen and the carbon dioxide into glucose. The plant then releases the oxygen back into the air, and stores energy within the glucose molecules.
Chlorophyll
Inside the plant cell are small organelles called chloroplasts, which store the energy of sunlight. Within the thylakoid membranes of the chloroplast is a light-absorbing pigment called chlorophyll, which is responsible for giving the plant its green color. During photosynthesis, chlorophyll absorbs energy from blue- and red-light waves, and reflects green-light waves, making the plant appear green.
Light-dependent Reactions vs. Light-independent Reactions
While there are many steps behind the process of photosynthesis, it can be broken down into two major stages: light-dependent reactions and light-independent reactions. The light-dependent reaction takes place within the thylakoid membrane and requires a steady stream of sunlight, hence the name light-dependent reaction. The chlorophyll absorbs energy from the light waves, which is converted into chemical energy in the form of the molecules ATP and NADPH. The light-independent stage, also known as the Calvin cycle, takes place in the stroma, the space between the thylakoid membranes and the chloroplast membranes, and does not require light, hence the name light-independent reaction. During this stage, energy from the ATP and NADPH molecules is used to assemble carbohydrate molecules, like glucose, from carbon dioxide.
C3 and C4 Photosynthesis
Not all forms of photosynthesis are created equal, however. There are different types of photosynthesis, including C3 photosynthesis and C4 photosynthesis. C3 photosynthesis is used by the majority of plants. It involves producing a three-carbon compound called 3-phosphoglyceric acid during the Calvin Cycle, which goes on to become glucose. C4 photosynthesis, on the other hand, produces a four-carbon intermediate compound, which splits into carbon dioxide and a three-carbon compound during the Calvin Cycle. A benefit of C4 photosynthesis is that by producing higher levels of carbon, it allows plants to thrive in environments without much light or water.
#17 This is Cool » Monaco » 2026-01-22 20:35:29
- Jai Ganesh
- Replies: 0
Monaco
Gist
Monaco is famous for its extreme wealth, luxury lifestyle, tax haven status (no income tax for residents), glamorous casinos (like the Monte Carlo Casino), yacht-filled harbors, and high-profile events like the Formula 1 Monaco Grand Prix, attracting the world's rich and famous to its French Riviera location, says TATA AIG, Wikipedia, and Study.com. As the world's second-smallest country, it's a major banking center, a hub for high-end tourism, and home to the ruling Grimaldi family, blending historic charm with modern sophistication.
The Monaco permanent residency card ("Carte de Sejour") allow applicants to live in Monaco indefinitely. Permanent residency is granted on the basis of demonstrating proof of accommodation and proof of financial self-sufficiency.
Summary
Monaco, officially the Principality of Monaco, is a sovereign city-state and microstate in Western Europe. Situated on the French Riviera, it is a semi-enclave bordered by France to the north, east, and west, with the Mediterranean Sea to the south; the Italian region of Liguria is about 15 km (9.3 mi) east. With a population of 38,423 living in an area of 2.08 sq km (0.80 sq mi), Monaco is the second smallest sovereign state in the world, after Vatican City, as well as the most densely populated. It also has the world's shortest national coastline of any non-landlocked nation, at 3.83 km (2.38 mi). Fewer than 10,000 of its residents are Monégasque nationals. Although French is the official language of Monaco, Italian and Monégasque are also widely spoken and understood.
Monaco is governed under a form of semi-constitutional monarchy, with Prince Albert II as head of state, who holds substantial political powers. The prime minister, who is the head of government, can be either a Monégasque or French citizen; the monarch consults with the Government of France before an appointment. Key members of the judiciary are detached French magistrates. The House of Grimaldi has ruled Monaco, with brief interruptions, since 1297. The state's sovereignty was officially recognised by the Franco-Monégasque Treaty of 1861, with Monaco becoming a full United Nations voting member in 1993. Despite Monaco's independence and separate foreign policy, its defence is the responsibility of France, notwithstanding two small military units.
Monaco is recognised as one of the wealthiest and most expensive places in the world. Its economic development was spurred in the late 19th century with the opening of the state's first casino, the Monte Carlo Casino, and a rail connection to Paris. The country's mild climate, scenery, and gambling facilities contributed to its status as a tourist destination and recreation centre for the wealthy. Monaco has become a major banking centre and sought to diversify into the services sector and small, high-value-added, non-polluting industries. Monaco is a tax haven; it has no personal income tax (except for French citizens) and low business taxes. Over 30% of residents are millionaires, with real estate prices reaching €100,000 ($116,374) per square metre in 2018. Monaco is a global hub of money laundering, and in June 2024 the Financial Action Task Force placed Monaco under increased monitoring to combat money laundering and terrorist financing.
Monaco is among the 46 Member States which constitute the Council of Europe. It is not part of the European Union (EU), but participates in certain EU policies, including customs and border controls. Through its relationship with France, Monaco uses the euro as its sole currency. Monaco joined the Council of Europe in 2004 and is a member of the Organisation internationale de la Francophonie (OIF). It hosts the annual motor race, the Monaco Grand Prix, one of the original Grands Prix of Formula One. The local motorsports association gives its name to the Monte Carlo Rally, hosted in January in the French Alps. The principality has a club football team, AS Monaco, which competes in French Ligue 1 and has been French champions on multiple occasions, as well as a basketball team, which plays in the EuroLeague. Monaco is a centre of marine conservation and research, being home to one of the world's first protected marine habitats, an Oceanographic Museum, and the International Atomic Energy Agency Marine Environment Laboratories, the only marine laboratory in the UN system.
Details
Monaco is a sovereign principality located along the Mediterranean Sea in the midst of the resort area of the Côte d’Azur (French Riviera). The city of Nice, France, lies 9 miles (15 km) to the west, the Italian border 5 miles (8 km) to the east. Monaco’s tiny territory occupies a set of densely clustered hills and a headland that looks southward over the Mediterranean. Many unusual features, however, have made Monaco among the most luxurious tourist resorts in the world and have given it a fame far exceeding its size.
Many visitors to Monaco alternate their hours between its beaches and boating facilities, its international sports-car races, and its world-famous Place du Casino, the gambling centre in the Monte-Carlo section that made Monte-Carlo an international byword for the extravagant display and reckless dispersal of wealth. The country has a mild Mediterranean climate with annual temperatures averaging 61 °F (16 °C) and with only about 60 days of rainfall. Monthly average temperatures range from 50 °F (10 °C) in January to 75 °F (24 °C) in August.
Evidences of Stone Age settlements in Monaco are preserved in the principality’s Museum of Prehistoric Anthropology. In ancient times the headland was known to the Phoenicians, Greeks, Carthaginians, and Romans. In 1191 the Genoese took possession of it, and in 1297 the long reign of the Grimaldi family began. The Grimaldis allied themselves with France except for the period from 1524 to 1641, when they were under the protection of Spain. In 1793 they were dispossessed by the French Revolutionary regime, and Monaco was annexed to France. With the fall of Napoleon I, however, the Grimaldis returned; the Congress of Vienna (1815) put Monaco under the protection of Sardinia. The principality lost the neighboring towns of Menton and Roquebrune in 1848 and finally ceded them to France under the terms of the Franco-Monegasque treaty of 1861. The treaty did restore Monaco’s independence, however, and in 1865 a customs union was established between the two countries. Another treaty that was made with France, in 1918, contained a clause providing that, in the event that the Grimaldi dynasty should become extinct, Monaco would become an autonomous state under French protection. A revision to the constitution in 2002 added females and their legitimate children to the line of succession. In 1997 the Grimaldi family commemorated 700 years of rule, and in 1999 Prince Rainier III marked 50 years on the throne. Upon his death in April 2005, he was succeeded by his son, Albert; Albert formally assumed the throne on July 12, 2005. The principality joined the United Nations in 1993. Though not a member of the European Union (EU), Monaco phased out the French franc for the single European currency of the euro by 2002.
Monaco’s refusal to impose income taxes on its residents and on international businesses that have established headquarters in the principality led to a severe crisis with France in 1962. A compromise was reached by which French citizens with less than five years residence in Monaco were taxed at French rates and taxes were imposed on Monegasque companies doing more than 25 percent of their business outside the principality. In the early 21st century, some European nations criticized Monaco’s loose banking regulations, claiming that the principality sheltered tax evaders and money launderers. In 2002 the Organisation for Economic Co-operation and Development (OECD) added Monaco to its “blacklist” of uncooperative tax havens. The principality was removed from the blacklist in 2009 after committing to OECD transparency standards.
Monaco’s constitution of 1911 provided for an elected National Council, but in 1959 Prince Rainier III suspended part of the constitution and dissolved the National Council because of a disagreement over the budget. In 1961 he appointed instead a national assembly. The aforementioned crisis of 1962 with France led him to restore the National Council and to grant a new, liberal constitution. The council comprises 18 members, elected by universal suffrage for a term of five years. Government is carried on by a minister of state (who must be a French citizen) and three state councillors acting under the authority of the prince, who is the official chief of state. Legislative power is shared by the prince and the National Council. Since 1819 the judicial system has been based on that of France; since 1962 the highest judicial authority has been the Supreme Tribunal.
A substantial portion of the government’s revenues comes from taxes on commercial transactions; additional revenue is drawn from franchises on radio, television, and the casino, from state-operated monopolies on tobacco and postage stamps, from sales taxes, and from the taxes imposed since 1962.
Monaco’s chief industry is tourism, and its facilities make it one of Europe’s most luxurious resorts. Once a winter attraction, it now draws summer visitors as well to its beaches and expanded mooring facilities. Business conferences are especially important. The social life of Monte-Carlo revolves around the Place du Casino. The casino was built in 1861, and in 1967 its operations were taken over by the principality. Banking and finance and real estate are other important components of the diverse services sector.
More than one-fourth of Monaco’s population is composed of French citizens, and a smaller but significant number are Italian, Swiss, and Belgian. Only about one-fifth of the population claims Monegasque descent. Most of the people are Roman Catholics. The official language is French.
The four sections, or quartiers, of Monaco are the town of Monaco, or “the Rock,” a headland jutting into the sea on which the old town is located; La Condamine, the business district on the west of the bay, with its natural harbor; Monte-Carlo, including the gambling casino; and the newer zone of Fontvieille, in which various light industries have developed.
In Monaco are the Roman Catholic cathedral, the prince’s Genoese and Renaissance palace, and the Oceanographic Museum of Monaco, built in 1910. The casino itself contains a theater designed by the 19th-century French architect Charles Garnier, which is the home of the Opéra de Monte Carlo. During the 1920s many of the works of the famous Ballets Russes of Serge Diaghilev were given their premieres there. There is also a Monte-Carlo national orchestra. The best known of the automobile events held in the principality are the Monte-Carlo Rally and the Grand Prix de Monaco.
Additional Information
Monaco is the second-smallest independent state in the world. It is a playground for tourists and a haven for the wealthy, the former drawn by its climate and the beauty of its setting and the latter by its advantageous tax regime.
The country - a constitutional monarchy - is surrounded on three sides by France.
Tourism is a major earner for the economy. The country is also a major banking centre and closely guards the privacy of its clients. Monaco does not levy income tax on its residents.
Its sovereignty was officially recognised by the Franco-Monegasque Treaty of 1861, with Monaco becoming a full United Nations voting member in 1993.

#18 Science HQ » Dura Mater » 2026-01-22 18:44:20
- Jai Ganesh
- Replies: 0
Dura Mater
Gist
The tough outer layer of tissue that covers and protects the brain and spinal cord and is closest to the skull.
The meningeal layer of the dura mater creates several dural folds that divide the cranial cavity into freely communicating spaces. The function of the dural folds is to limit the rotational displacement of the brain. The folds include the following: The falx cerebri is a meningeal projection of dura in the brain.
Dura is the thick outer most layer of the 3 meninges. The thick fibrous dura surrounds, supports and protects the central nervous system (brain and spinal cord). In the cranium the dura forms folds to form partitions of the cranial cavity, and separates in places to form dural venous sinuses.
Summary
The dura mater (or just dura) is the outermost of the three meningeal membranes. The dura mater has two layers, an outer periosteal layer closely adhered to the neurocranium, and an inner meningeal layer known as the dural border cell layer. The two dural layers are for the most part fused together forming a thick fibrous tissue membrane that covers the brain and the vertebrae of the spinal column. But the layers are separated at the dural venous sinuses to allow blood to drain from the brain. The dura covers the arachnoid mater and the pia mater, the other two meninges, in protecting the central nervous system.
At major boundaries of brain regions such as the longitudinal fissure between the hemispheres, and the tentorium cerebelli between the posterior brain and the cerebellum the dura separates, folds and invaginates to make the divisions. These folds are known as dural folds, or reflections.
The dura mater is primarily derived from neural crest cells, with postnatal contributions from the paraxial mesoderm.
Details
The meninges are three layers of connective tissue that surround, support and protect the central nervous system (brain and spinal cord). From superficial to deep these layers are named the dura, arachnoid and pia. The dura mater is a thick, tough, fibrous membrane. It receives blood and nerve supply from the meningeal arteries, veins and nerves.
Cranial dura mater
In the cranium, the dura consists of two layers; an outer periosteal dura and an inner meningeal dura. The periosteal dura is closely attached to the internal surface of the skull bones while the inner meningeal dura is continuous with the dura of the spinal cord. The periosteal dura and meningeal dura are tightly fused together, except in a few places where they separate to form the dural venous sinuses; spaces that collect venous blood from the large veins of the brain. The dural venous sinuses are named as follows; superior sagittal sinus, inferior sagittal sinus, straight sinus, occipital sinus, transverse sinus, sigmoid sinus, marginal sinus, superior petrosal sinus, inferior petrosal sinus, petrosquamous sinus, cavernous sinus, sphenoparietal sinus, intercavernous sinus. The straight, occipital, transverse and superior sagittal sinuses all meet at the confluence of the sinuses. Arachnoid granulations, small tufts of arachnoid, protrude through the dura mater into the dural venous sinuses. They are the site of cerebrospinal fluid absorption into dural venous sinuses. Another feature of cranial dura are the dural folds. These are reflections of the inner meningeal dura which divide the cranium into separate compartments. The four dural folds are the falx cerebri, tentorium cerebelli, falx cerebelli, diaphragma sellae; in brief, they separate the cerebral and cerebellar hemispheres into divisions.
Spinal dura mater
In the spinal cord, only one layer of dura mater is found. Unlike in the cranium, the dura is not closely integrated with the overlying bones. Instead, a space exists between the dura and the vertebral bones known as the epidural space. The inferior aspect of the spinal dural sac is anchored to the coccyx by a thin connective tissue strand called the filum terminale.
Innervation
The innervation of the cranial dura mater is primarily sourced from the trigeminal (CN V) and vagus CN X) nerves, as well as spinal nerves C2/C3.
Trigeminal nerve
Several branches of the trigeminal nerve supply the dura mater:
* The tentorial branch of the ophthalmic nerve (CN V1), also known as the recurrent meningeal branch, supplies much of the supratentorial dura mater (i.e., posterior half of the falx cerebri, calvarial dura and superior surface of the tentorium cerebelli).
* The meningeal branch of the anterior ethmoidal nerve (branch of the nasociliary nerve (ophthalmic nerve)) supplies the central region of the anterior cranial fossa as well as anterior parts of the falx cerebri.
* The meningeal branch of the maxillary nerve (CN V2) provides innervation to the posterior region of the anterior cranial fossa as well as the anterior portion of the middle cranial fossa.
* The meningeal branch of the mandibular nerve (CN V3) supplies the posterolateral parts of the middle cranial fossa, before extending anteriorly to the lateral region of the anterior cranial fossa.
Vagus nerve
The posterior and lateral regions of the posterior cranial fossa and inferior surface of the tentorium cerebelli are all primarily innervated by the meningeal branch of the vagus nerve (which arises from its superior ganglion).
Spinal nerves C2/C3
The central region of the posterior cranial fossa, around the foramen magnum, receives innervation from sensory nerve fibers whose cell bodies are located in the spinal ganglia of spinal nerves C2/C3. The nerves may present as ascending branches of the meningeal branch of these spinal nerves which ascend the vertebral canal into the cranial cavity, via the foramen magnum. Alternatively, communicating branches of spinal nerves C2/C3 may pass to the hypoglossal nerve (CN XII), entering the cranial cavity via the meningeal branch of the hypoglossal nerve (via the hypoglossal canal). Some references occasionally also describe meningeal branches derived from the facial (CN VII) and glossopharyngeal (CN IX) nerves as supplying the posterior cranial fossa, however this remains debated.
Spinal dura
The innervation of the spinal dura mater is derived from a meningeal branch of each spinal nerve. It arises near the division of the spinal nerve into anterior and posterior rami, close to the gray/white rami communicating branches, before coursing through the intervertebral foramen into the vertebral canal.
Additional Information
The brain is an important part of the human body, as it performs vital functions and controls almost all bodily functions. It is protected by a strong framework of bones, called the skull. Besides this bony structure, it is also protected against several kinds of injuries or head traumas by the meninges, which are three-layered membranous structures that help protect the brain parts from damage.
The outermost layer of the meninges is the dura mater. The other two layers are collectively known as the leptomeninges and consist of the arachnoid mater (middle layer) and the pia mater (innermost layer). The dura mater is frequently known as the dura.
The dura protects its vital underlying components with a strong fibrous protective covering. In aspects of compressive impacts due to mass lesions and related edema, the compartmentalization of the brain through the help of dural reflections is especially important. The connection of the dural layers to each other, and the underlying leptomeninges and calvarium, has a huge impact on scientists’ knowledge of the impacts of intracranial injury.
Summary:
* The meninges safeguard the spinal cord and brain from tissue injury and assist the framework of the blood vessels
* Dura mater is on the outermost end of the meninges, situated directly beneath the skull and the bones of the vertebral column
* The dura mater is made up of two layers of connective tissue: the periosteal layer and the meningeal layer
* The periosteal layer lines the inner surface of the cranium’s bones. The periosteum is a dense fibrous membrane that covers the surface areas of bones
* The meningeal layer is found deep within the periosteal layer
* The dura mater has a vascular supply of its own
* The dura mater’s meningeal layer bends towards the inner direction of itself to form 4 structural forms, called the dural reflections
* The 4 dural reflections are: Diaphagma sellae, Falx cerebri, Tentorium cerebelli, and Falx cerebelli
* Dura mater encircles and continues to support the large venous channels (called dural sinuses) that help in carrying the blood from the brain to the heart.
* Haemorrhage, meningitis, and meningiomas are some complications involving the dura mater.
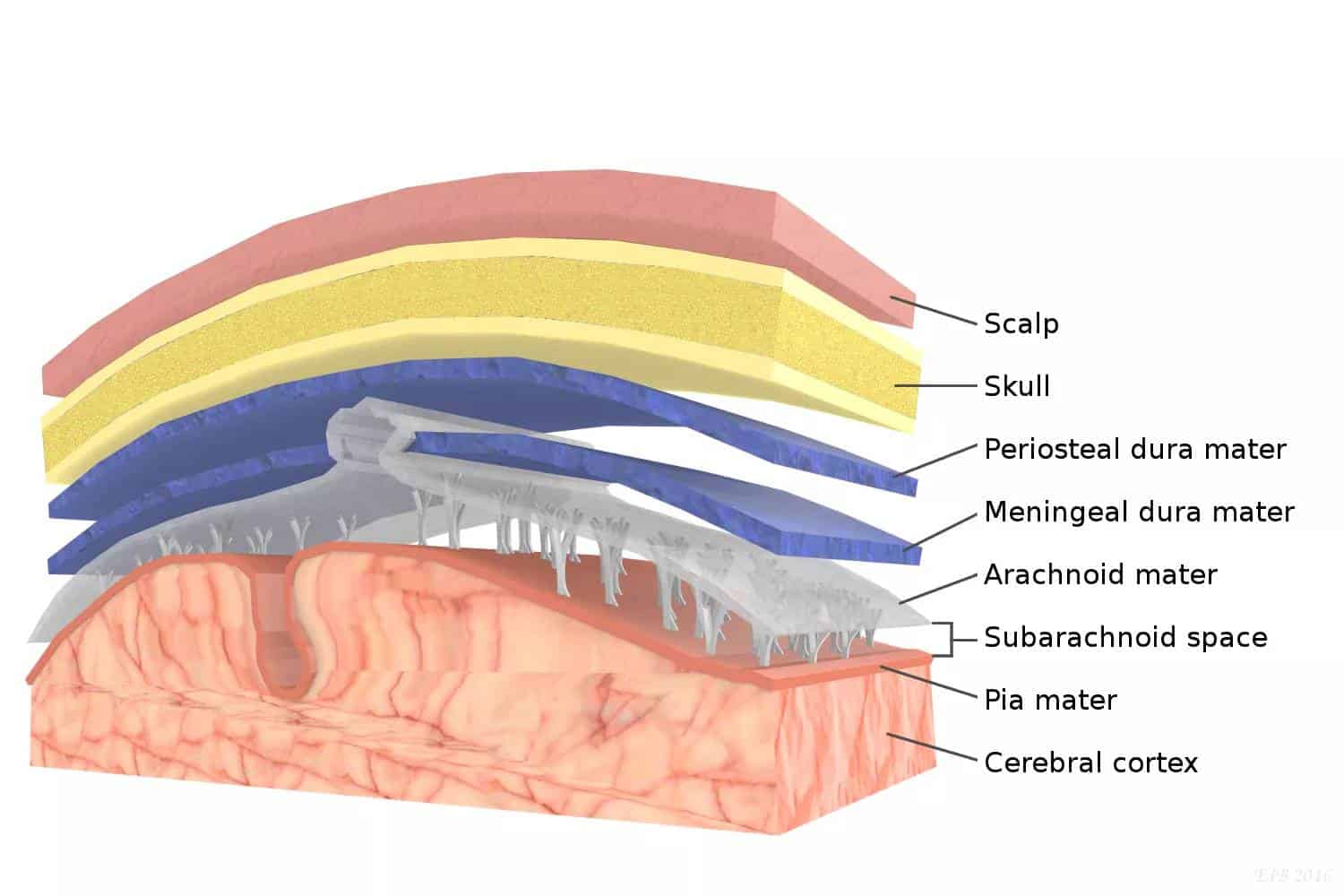
#19 Re: Dark Discussions at Cafe Infinity » crème de la crème » 2026-01-22 18:06:17
2417) Donald Glaser
Gist:
Life
Donald Glaser was born in Cleveland, Ohio to Russian immigrants. His father was a businessman. After first studying at Case School of Applied Science in Cleveland, he later received his PhD in physics from California Institute of Technology, Pasadena, in 1949. He then moved to the University of Michigan in Ann Arbor, where he carried out the research that led to his Nobel Prize, before moving to the University of California, Berkeley, in 1959. Beginning in the 1960s, Glaser devoted himself to molecular biology. He was married twice and had two children from his first marriage.
Work
Our ability to study the smallest components of our world took a giant leap forward when C.T.R. Wilson invented the cloud chamber, where the trails of charged particles can be observed. Donald Glaser's invention of the bubble chamber in 1952 made it possible to study particles with higher energies. When charged particles rush forward through the chamber filled with a liquid at near-boiling point, they ionize atoms they pass by. When the pressure inside the chamber is then reduced, bubbles form around these charged atoms. The particles' tracks can then be photographed and analyzed.
Summary
Donald A. Glaser (born September 21, 1926, Cleveland, Ohio, U.S.—died February 28, 2013, Berkeley, California) was an American physicist and recipient of the 1960 Nobel Prize for Physics for his invention (1952) and development of the bubble chamber, a research instrument used in high-energy physics laboratories to observe the behaviour of subatomic particles.
After graduating from Case Institute of Technology, Cleveland, in 1946, Glaser attended the California Institute of Technology, Pasadena, where he received a Ph.D. in physics and mathematics in 1950. He then began teaching at the University of Michigan, where he became a professor in 1957.
Glaser conducted research with Nobelist Carl Anderson, who was using cloud chambers to study cosmic rays. Glaser, recognizing that cloud chambers had a number of limitations, created a bubble chamber to learn about the pathways of subatomic particles. Because of the relatively high density of the bubble-chamber liquid (as opposed to the vapour that filled cloud chambers), collisions producing rare reactions were more frequent and were observable in finer detail. New collisions could be recorded every few seconds when the chamber was exposed to bursts of high-speed particles from particle accelerators. As a result, physicists were able to discover the existence of a host of new particles, notably quarks. At the age of 34, Glaser became one of the youngest scientists ever to be awarded a Nobel Prize.
In 1959 Glaser joined the staff of the University of California, Berkeley, where he became a professor of physics and molecular biology in 1964. In 1971 he cofounded the Cetus Corp., a biotechnology company that developed interleukin-2 and interferon for cancer therapy. The firm was sold (1991) to Chiron Corp., which was later acquired by Novartis. In the 1980s Glaser turned to the field of neurobiology and conducted experiments on vision and how it is processed by the human brain.
Details
Donald Arthur Glaser (September 21, 1926 – February 28, 2013) was an American physicist and biologist who received the Nobel Prize in Physics in 1960 for his invention of the bubble chamber.
Personal life
Donald Arthur Glaser was born on September 21, 1926, in Cleveland, Ohio, to Russian Jewish immigrants, Lena and William J. Glaser, a businessman. He enjoyed music and played the piano, violin, and viola. He went to Cleveland Heights High School, where he became interested in physics as a means to understand the physical world. He died in his sleep at the age of 86 on February 28, 2013, in Berkeley, California.
Education and career
Glaser attended Case School of Applied Science (now Case Western Reserve University), where he completed his Bachelor of Science degree in physics and mathematics in 1946. During the course of his education there, he became especially interested in particle physics. He played viola in the Cleveland Philharmonic while at Case, and taught mathematics classes at the college after graduation. He continued on to the California Institute of Technology (Caltech), where he pursued his PhD in physics. His interest in particle physics led him to work with Nobel laureate Carl David Anderson, studying cosmic rays with cloud chambers. He preferred the accessibility of cosmic ray research over that of nuclear physics. While at Caltech he learned to design and build the equipment he needed for his experiments, and this skill would prove to be useful throughout his career. He also attended molecular genetics seminars led by Nobel laureate Max Delbrück; he would return to this field later. Glaser completed his doctoral thesis, The Momentum Distribution of Charged Cosmic Ray Particles Near Sea Level, after starting as an instructor at the University of Michigan in 1949. He received his PhD from Caltech in 1950, and he was promoted to professor at Michigan in 1957 He joined the faculty of UC Berkeley in 1959 as a professor of physics. During this time, his research concerned short-lived elementary particles. The bubble chamber enabled him to observe the paths and lifetimes of the particles. Starting in 1962, Glaser changed his field of research to molecular biology, starting with a project on ultraviolet-induced cancer. In 1964, he was given the additional title of professor of molecular biology. Glaser's position (since 1989) was professor of physics and neurobiology in the graduate school.
Bubble chamber
While teaching at Michigan, Glaser began to work on experiments that led to the creation of the bubble chamber. His experience with cloud chambers at Caltech had shown him that they were inadequate for studying elementary particles. In a cloud chamber, particles pass through gas and collide with metal plates that obscure the scientists' view of the event. The cloud chamber also needs time to reset between recording events and cannot keep up with accelerators' rate of particle production.
He experimented with using superheated liquid in a glass chamber. Charged particles would leave a track of bubbles as they passed through the liquid, and their tracks could be photographed. He created the first bubble chamber with ether. He experimented with hydrogen while visiting the University of Chicago, showing that hydrogen would also work in the chamber.
It has often been claimed that Glaser was inspired to his invention by the bubbles in a glass of beer; however, in a 2006 talk, he refuted this story, saying that although beer was not the inspiration for the bubble chamber, he did experiments using beer to fill early prototypes.
His new invention was ideal for use with high-energy accelerators, so Glaser traveled to Brookhaven National Laboratory with some students to study elementary particles using the accelerator there. The images that he created with his bubble chamber brought recognition of the importance of his device, and he was able to get funding to continue experimenting with larger chambers. Glaser was then recruited by Nobel laureate Luis Alvarez, who was working on a hydrogen bubble chamber at the University of California at Berkeley. Glaser accepted an offer to become a professor of physics there in 1959.
Nobel Prize
Glaser was awarded the 1960 Nobel Prize for Physics for the invention of the bubble chamber. His invention allowed scientists to observe what happens to high-energy beams from an accelerator, thus paving the way for many important discoveries.

#20 Dark Discussions at Cafe Infinity » Colonial Quotes » 2026-01-22 16:22:31
- Jai Ganesh
- Replies: 0
Colonial Quotes
1. Communists have always played an active role in the fight by colonial countries for their freedom, because the short-term objects of Communism would always correspond with the long-term objects of freedom movements. - Nelson Mandela
2. Why are we, as a nation so obsessed with foreign things? Is it a legacy of our colonial years? We want foreign television sets. We want foreign shirts. We want foreign technology. Why this obsession with everything imported? - A. P. J. Abdul Kalam
3. The skills you need to fight the colonial power and the skills you need to gain independence are not necessarily the same you need to run a country. - Kofi Annan
4. Was it not enough punishment and suffering in history that we were uprooted and made helpless slaves not only in new colonial outposts but also domestically. - Robert Mugabe
5. All the sparrows on the rooftops are crying about the fact that the most imperialist nation that is supporting the colonial regime in the colonies is the United States of America. - Nikita Khrushchev
6. Thankfully, Australia has emerged from its inauspicious colonial beginnings to become a proud nation, a nation that overcame those primeval prejudices. - Rupert Murdoch
7. England was the first true colonial power to use its dominion over a large part of Africa, the Middle East, Asia, Australia, North America, and many Caribbean islands, in the first half of the 20th century. - Fidel Castro
8. Famines were frequent in colonial India and some estimates indicate that 30 to 40 million died out of starvation in Tamil Nadu, Bihar and Bengal during the later half of the 19th century. - M. S. Swaminathan.
#21 Re: Jai Ganesh's Puzzles » General Quiz » 2026-01-22 15:53:47
Hi,
#10713. What does the term in Geography Couloir mean?
#10714.. What does the term in Geography Country mean?
#22 Re: Jai Ganesh's Puzzles » English language puzzles » 2026-01-22 15:39:26
Hi,
#5909. What does the noun homestead mean?
#5910. What does the adjective homely mean?
#23 Re: Jai Ganesh's Puzzles » Doc, Doc! » 2026-01-22 15:25:02
Hi,
#2551. What does the medical term Floaters or eye floaters mean?
#24 Jokes » Cherry Jokes - III » 2026-01-22 15:01:47
- Jai Ganesh
- Replies: 0
Q: How do you strike fear into a pie?
A: With a very cherry movie.
* * *
Q: Why were the little cherries upset?
A: Because their parents were in a jam!
* * *
Q: How many grams of protein are in a cherry pi?
A: 3.14159265
* * *
Q: What do you call a fruit that likes to tell jokes?
A: Cherry Seinfeld. Did you hear about the cherry that liked to explode? It was da bomb.
* * *
Q: What do you call a man that can't stop eating cherries whole?
A: A bottomless pit.
* * *
#25 Re: Jai Ganesh's Puzzles » 10 second questions » 2026-01-22 14:49:37
Hi,
#9835.