Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2007-11-30 05:21:32
- Math Student
- Guest
Vectors - Prove that A,B and D are on a straight line
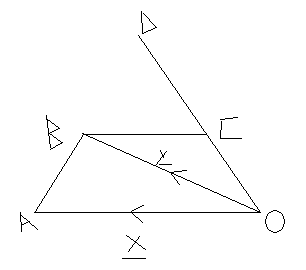
This is the information I've got
OA = x
OB = y
BC = 3/4AO
OD = 4OC
I now need to prove that A, B and D lie on a straight line.
I'm not sure how I'm supposed to go about this. Could you show me, or at least tell me where to start?
I've worked out that:
AB = y-x
BC = 3/4-x
OC = y+3/4-x
AD = 4y-3x
Thank you in advance for your much appreciated assistance.
#2 2007-11-30 05:54:51
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Vectors - Prove that A,B and D are on a straight line
Everything's right apart from AD. In fact, your result for AD would be enough to prove that ABD is not a straight line.
I'm not sure what your method was, but here's one way:
AD = AO + OD
= AO +4OC
= -x + 4(y-3/4x)
= -x +4y - 3x
= -4x + 4y
= 4(y-x)
= 4AB
Hence AD is a scalar multiple of AB, and so A, B and D lie in a straight line.
Why did the vector cross the road?
It wanted to be normal.
Offline
#3 2007-11-30 05:55:08
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: Vectors - Prove that A,B and D are on a straight line
Another way.
Mark the point E on AO such that AE = (3⁄4)AO. Then the triangles OEC and OAD are similar (because |OE|:|OA| = |OC|:|OD| = 1:4). Hence angle OAD = angle OEC. But angle OEC = angle OAB (because ABCE is a parallelogram). Therefore angle OAD = angle OAB from which we can conclude that A, B and D are collinear.
Last edited by JaneFairfax (2007-11-30 05:55:56)
Offline
#4 2007-11-30 10:42:33
- Math Student
- Guest
Re: Vectors - Prove that A,B and D are on a straight line
Hehe, thanks! I redid my working out and found out that Part 4 was wrong. I found that the gradients were the same eventually. Thank you for the help anyway.