Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2024-03-13 00:22:57
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,897
Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel
Gist
Hilbert's paradox is a veridical paradox: it leads to a counter-intuitive result that is provably true. The statements "there is a guest to every room" and "no more guests can be accommodated" are not equivalent when there are infinitely many rooms.
Details:
Hilbert's Paradox
Hilbert's paradox of the Grand Hotel (colloquial: Infinite Hotel Paradox or Hilbert's Hotel) is a thought experiment which illustrates a counterintuitive property of infinite sets. It is demonstrated that a fully occupied hotel with infinitely many rooms may still accommodate additional guests, even infinitely many of them, and this process may be repeated infinitely often. The idea was introduced by David Hilbert in a 1925 lecture "Über das Unendliche", reprinted in (Hilbert 2013, p.730), and was popularized through George Gamow's 1947 book One Two Three... Infinity.
The paradox
Hilbert imagines a hypothetical hotel with rooms numbered 1, 2, 3, and so on with no upper limit. This is called a countably infinite number of rooms. Initially every room is occupied, and yet new visitors arrive, each expecting their own room. A normal, finite hotel could not accommodate new guests once every room is full. However, it can be shown that the existing guests and newcomers — even an infinite number of them — can each have their own room in the infinite hotel.
Finitely many new guests
With one additional guest, the hotel can accommodate them and the existing guests if infinitely many guests simultaneously move rooms. The guest currently in room 1 moves to room 2, the guest currently in room 2 to room 3, and so on, moving every guest from their current room n to room n+1. The infinite hotel has no final room, so every guest has a room to go to. After this, room 1 is empty and the new guest can be moved into that room. By repeating this procedure, it is possible to make room for any finite number of new guests. In general, when k guests seek a room, the hotel can apply the same procedure and move every guest from room n to room n + k.
Infinitely many new guests
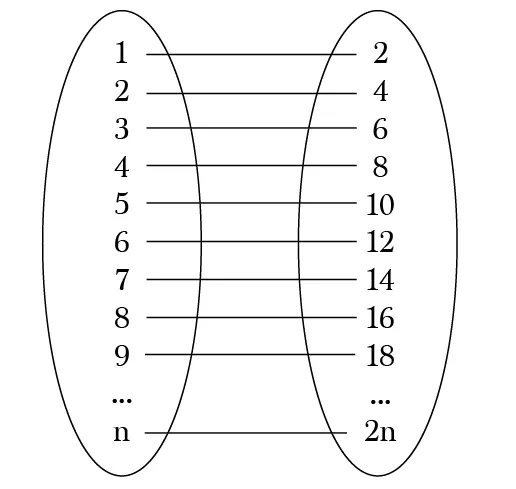
It is also possible to accommodate a countably infinite number of new guests: just move the person occupying room 1 to room 2, the guest occupying room 2 to room 4, and, in general, the guest occupying room n to room 2n (2 times n), and all the odd-numbered rooms (which are countably infinite) will be free for the new guests.
Additional Information
What does Countably Infinite mean?
A set is countably infinite if it has a one-to-one correspondence with the natural numbers (you know 1,2,3,4,…).
Don’t let that definition confuse you, if you read the last post on infinity, you’re already familiar with countably infinite sets.
Remember how we proved that the set of all even numbers is the same size (aka: cardinality) as the set of natural numbers? We discovered this by making a one-to-one mapping between the sets. Well that’s all countably infinite means! Simply that we can match them up one by one with the counting numbers, which is infinite.
A Crafty Solution
Now this is perplexing. At first you may think, “Well since it’s infinite can’t we just put the new guest in the last room?” Except since it’s infinite there really isn’t a last room and even if we were to locate that room it’s occupied.
The trick to solving this problem is to make a mapping from our countably infinite set of rooms to another countably infinite set of rooms that leaves us with an extra unoccupied room.
That sounds confusing but it is similar to how we proved the set of all even numbers was the same size as the set of natural numbers.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#2 2024-03-13 03:23:17
- Europe2048
- Member
- Registered: 2024-01-03
- Posts: 41
Re: Hilbert's paradox of the Grand Hotel
It is also possible to accommodate an infinite amount of infinitely many guests, like if you had infinitely many buses with infinitely many guests in each:
**|01 02 03 04 05 ...
--+------------------
01|01 02 06 07 15 ...
02|03 05 08 14 16 ...
03|04 09 13 17 25 ...
04|10 12 18 24 30 ...
05|11 19 23 31 39 ...
..|.. .. .. .. .. ...Offline
#3 2024-03-13 16:48:21
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,897
Re: Hilbert's paradox of the Grand Hotel
The Infinite Hotel Paradox
Mathematicians and scientists have always been intrigued by the mysteries behind ‘infinity’. The Hilbert’s paradox of an infinite hotel is one such thought experiment that arouses curiosity and intrigues people to this day.
Imagine that your boss asked you to go on an urgent business trip to one of the busiest places in the country. The first thing you would do is book your tickets and look up a hotel with available rooms. Alas! After two hours of searching, you find that all the hotels are full.
Suddenly, an ‘Infinite Hotel’ advertisement comes up, so you visit the website and manage to find a room for yourself, even if the hotel is full.
Now, you might begin to wonder… what is this infinite hotel exactly? How is it possible that, despite having no vacancy, vacant rooms can still be arranged for guests? It’s contradictory to logic!
Infinity Is Vague
The concept of infinity is interesting and requires you to have an open mind while exploring various aspects of it. Mathematics is such that it needs you to give up your pre-assumed notions and dive into the unknown.
Infinity is a vague concept that implies endless possibilities, giving rise to a huge number of paradoxes. It could be appropriate to say that mathematicians have made this concept even more complex by introducing terms like ‘countably infinite’ and ‘uncountably infinite’.
On the one hand, we say that infinite things are unbounded and unfathomable, implying ‘uncountable infinite things’, and on the other hand, we consider a very large collection of things as ‘countably infinite’, which can be counted one at a time, even though it’s counting won’t come to an end. Isn’t that strange?
The ‘Infinite Hotel Paradox’
The ‘Infinite Hotel Paradox’ is one such thought experiment proposed by David Hilbert in 1924 that explores the infinite nature of numbers and the properties of an infinite set.
Let’s assume that there is a grand hotel called the ‘Infinite Hotel,’ which has a countably infinite number of occupied rooms. The rooms correspond to the natural numbers in the number series. Using common sense, one would conclude that since the hotel is completely occupied, no more guests can be accommodated, but here comes the twist with “infinity”.
Infinity is unbounded, so no matter how big the number is, there is always a bigger number. Thus, if you want a room there, the hotel manager can easily arrange it for you.
The ‘Infinite Hotel Paradox’
The ‘Infinite Hotel Paradox’ is one such thought experiment proposed by David Hilbert in 1924 that explores the infinite nature of numbers and the properties of an infinite set.
Let’s assume that there is a grand hotel called the ‘Infinite Hotel,’ which has a countably infinite number of occupied rooms. The rooms correspond to the natural numbers in the number series. Using common sense, one would conclude that since the hotel is completely occupied, no more guests can be accommodated, but here comes the twist with “infinity”.
Infinity is unbounded, so no matter how big the number is, there is always a bigger number. Thus, if you want a room there, the hotel manager can easily arrange it for you.
The Tricky Solution
There is no last room, but there always exists the next room in this Infinite Hotel. And therein lies the solution to accommodating extra guests into new rooms.
The clever manager can shift each guest to the immediate next room, simultaneously. For example, move the guest from room #1 to room #2, room #2 to room #3, room #3 to room #4, and so on. In this way, the guest in room #n is shifted to room #n+1.
In this way, after shifting every guest, room #1 is empty, where one more guest can be accommodated.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
Pages: 1