Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2021-12-07 20:51:45
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,620
Euler's polyhedron formula

Euler's polyhedron formula
Let's begin by introducing the protagonist of this story - Euler's formula:
V - E + F = 2.
Simple though it may look, this little formula encapsulates a fundamental property of those three-dimensional solids we call polyhedra, which have fascinated mathematicians for over 4000 years. Actually I can go further and say that Euler's formula tells us something very deep about shape and space. The formula bears the name of the famous Swiss mathematician Leonhard Euler (1707 - 1783), who would have celebrated his 300th birthday this year.
What is a polyhedron?
Before we examine what Euler's formula tells us, let's look at polyhedra in a bit more detail. A polyhedron is a solid object whose surface is made up of a number of flat faces which themselves are bordered by straight lines. Each face is in fact a polygon, a closed shape in the flat 2-dimensional plane made up of points joined by straight lines.
A polygon is called regular if all of its sides are the same length, and all the angles between them are the same; the triangle and square in figure 1 and the pentagon in figure 2 are regular.
A polyhedron is what you get when you move one dimension up. It is a closed, solid object whose surface is made up of a number of polygonal faces. We call the sides of these faces edges - two faces meet along each one of these edges. We call the corners of the faces vertices, so that any vertex lies on at least three different faces. To illustrate this, here are two examples of well-known polyhedra.
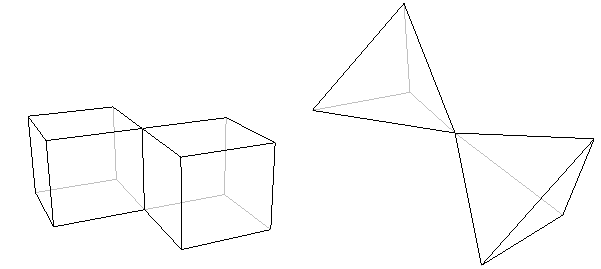
A polyhedron consists of just one piece. It cannot, for example, be made up of two (or more) basically separate parts joined by only an edge or a vertex. This means that neither of the following objects is a true polyhedron.
What does the formula tell us?
We're now ready to see what Euler's formula tells us about polyhedra. Look at a polyhedron, for example the cube or the icosahedron above, count the number of vertices it has, and call this number V. The cube, for example, has 8 vertices, so V = 8. Next, count the number of edges the polyhedron has, and call this number E. The cube has 12 edges, so in the case of the cube E = 12. Finally, count the number of faces and call it F. In the case of the cube, F = 6. Now Euler's formula tells us that
V - E + F = 2;
or, in words: the number of vertices, minus the number of edges, plus the number of faces, is equal to two.
In the case of the cube, we've already seen that V = 8, E = 12 and F = 6. So,
V - E + F = 8 - 12 + 6 = 14 - 12 = 2
which is what Euler's formula tells us it should be. If we now look at the icosahedron, we find that V = 12, E = 30 and F = 20. Now,
V - E + F = 12 - 30 + 20 = 32 - 30 = 2,
as we expected.
Euler's formula is true for the cube and the icosahedron. It turns out, rather beautifully, that it is true for pretty much every polyhedron. The only polyhedra for which it doesn't work are those that have holes running through them like the one shown in the figure below.
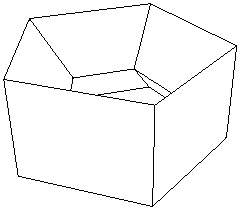
These polyhedra are called non-simple, in contrast to the ones that don't have holes, which are called simple. Non-simple polyhedra might not be the first to spring to mind, but there are many of them out there, and we can't get away from the fact that Euler's Formula doesn't work for any of them. However, even this awkward fact has become part of a whole new theory about space and shape.
The power of Euler's formula
Whenever mathematicians hit on an invariant feature, a property that is true for a whole class of objects, they know that they're onto something good. They use it to investigate what properties an individual object can have and to identify properties that all of them must have. Euler's formula can tell us, for example, that there is no simple polyhedron with exactly seven edges. You don't have to sit down with cardboard, scissors and glue to find this out - the formula is all you need. The argument showing that there is no seven-edged polyhedron is quite simple, so have a look at it if you're interested.
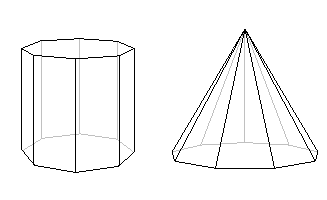
Using Euler's formula in a similar way we can discover that there is no simple polyhedron with ten faces and seventeen vertices. The prism shown below, which has an octagon as its base, does have ten faces, but the number of vertices here is sixteen. The pyramid, which has a 9-sided base, also has ten faces, but has ten vertices. But Euler's formula tells us that no simple polyhedron has exactly ten faces and seventeen vertices.
It's considerations like these that lead us to what's probably the most beautiful discovery of all. It involves the Platonic Solids, a well-known class of polyhedra named after the ancient Greek philosopher Plato, in whose writings they first appeared.
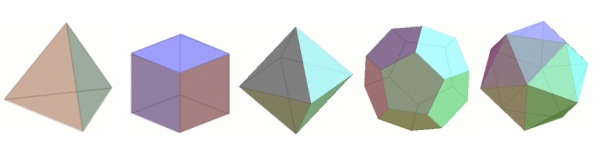
Although their symmetric elegance is immediately apparent when you look at the examples above, it's not actually that easy to pin it down in words. It turns out that it is described by two features. The first is that Platonic solids have no spikes or dips in them, so their shape is nice and rounded. In other words, this means that whenever you choose two points in a Platonic solid and draw a straight line between them, this piece of straight line will be completely contained within the solid — a Platonic solid is what is called convex. The second feature, called regularity, is that all the solid's faces are regular polygons with exactly the same number of sides, and that the same number of edges come out of each vertex of the solid.
The cube is regular, since all its faces are squares and exactly three edges come out of each vertex. You can verify for yourself that the tetrahedron, the octahedron, the icosahedron and the dodecahedron are also regular.
Now, you might wonder how many different Platonic Solids there are. Ever since the discovery of the cube and tetrahedron, mathematicians were so attracted by the elegance and symmetry of the Platonic Solids that they searched for more, and attempted to list all of them. This is where Euler's formula comes in. You can use it to find all the possibilities for the numbers of faces, edges and vertices of a regular polyhedron.What you will discover is that there are in fact only five different regular convex polyhedra! This is very surprising; after all, there is no limit to the number of different regular polygons, so why should we expect a limit here? The five Platonic Solids are the tetrahedron, the cube, the octahedron, the icosahedron and the dodecahedron shown above.
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
Pages: 1