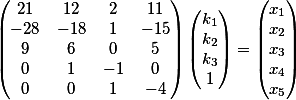Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2019-12-10 19:07:21
- VeryWell
- Member
- Registered: 2017-08-14
- Posts: 3
Dmitry Varlamov
Good day!
I am from Samara (Russia)
I know a little mathematics, but I already know how to create a general solution to any Diophantine equation, solve a system of Diophantine equations (linear with many variables), and create a Diophantine equation by its complete solution.
Online calculators created.
I am looking for like-minded people, critics, public offline sites to convey information.
Offline
#2 2019-12-10 20:26:58
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 52,735
Re: Dmitry Varlamov
Hi,
Welcome to the forum!
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#3 2019-12-10 22:15:56
- VeryWell
- Member
- Registered: 2017-08-14
- Posts: 3
Re: Dmitry Varlamov
Example
System of diophantine linear equation
Solve
Offline
Pages: 1
*x_{1}+(3)*x_{2}+(0)*x_{3}+(6)*x_{4}+(-5)*x_{5}=19\)
*x_{1}+(3)*x_{2}+(-7)*x_{3}+(12)*x_{4}+(-5)*x_{5}=17\)