Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2007-01-11 12:50:29
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
My ghost zombie convergency theorem!
I got this idea from a zombie video game my friend put together in gamemaker. The zombies are programmed to walk directly towards you at every moment, and they all have the same speed. Your job is of course to avoid and shoot them.
Anyway, something i noticed was as you are being persued by multiple zombies, and continue to flee, the zombies locations tend to converge at the same point, they congregate together and persue you from the same location. If the zombies can move inside eachother and are not blocked by eachothers pressence (which is why they have to be ghost zombies) then ultimately the zombies converge to the exact same spot and continue to persue you along the exact same path. As if it was just one zombie!
I thought, "if that is so, then it must be provable mathematically"
I think I've just about done it! I call it the Ghost Zombie Convergency theorem!
It states that if two or more zombies are persuing the same moving or none moving victim at the same speed, and the zombies are ghosts, they ultimately converge to the same location and follow the same path. There is one more rule to the theorem which i'll demonstrate.
Take a loook at this pic:
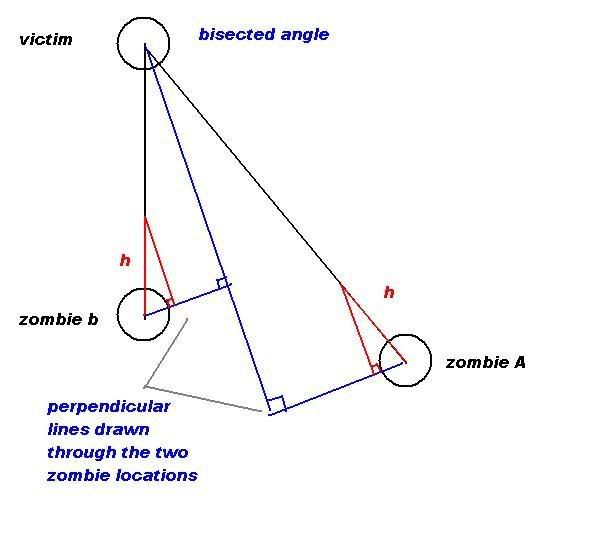
At the top is the victim who is a taget. Bottem right is zombie A and bottom left is zombie B.
Now Δ(distance_to_target) = velocityΔt as we know. Lets let h = Δ(distance_to_target)
The first step is to draw a line to bisect the angle formed by the intersecting paths of the zombies at the target. The next step is to draw two perpendicular lines through this line, that pass through the location of zombie A and zombie B respectively.
Now with a little geometry it can easily be proved that the two little red right triangles I drew are congruent. (I'll skip that part as its easy to do) Now if you look at the blue lines I drew, you can see how the horizontal distance between the two zombies will decrease by twice the measure of the short side of the red right triangles. (in relation to that blue line) As for the vertical blue line (the one that bisects the angle) the vertical componants are both increased by the same value. (the value of the long side of the red right triangle) if we think of the new distance between the two zombies as a hypotenuse of a right triangle with these horizontal and vertical componants, we see that one side remains the same while the other side shortens.
Thus the length of the hypotenuse is decreasing. (since sqrt(x) decreases as x decreases) Which is the distance between the two zombies. Hence the distance between the two zombies is constantly decreasing and they ultimately converge to the same point. Once they do, they're direction is determined by the location of the target, hence their paths are identical.
The only rule that needs to be mentioned is the angle between them has to be a none zero value. Otherwise the horizontal compoant of the red right triangle (which is perpendicular to the angle bisector line) has a value of zero. (since cos 90 = 0). Therefore, so long as the target does not remain in this sort of location indefinately, they will ultimately converge.
Somewhat informal proof of course, I hope i explained it clearly.
Last edited by mikau (2007-01-11 13:04:47)
A logarithm is just a misspelled algorithm.
Offline
#2 2007-01-11 17:08:21
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My ghost zombie convergency theorem!
In case you guys don't realize, we're mostly assuming the victim is fleeing and is never actually caught. However the theorem holds true if the victim is stationary as well.
A logarithm is just a misspelled algorithm.
Offline
#3 2007-01-11 19:12:05
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My ghost zombie convergency theorem!
Here's a gif of the convergence in action:

A logarithm is just a misspelled algorithm.
Offline
#4 2007-01-11 19:58:36
- Toast
- Real Member

- Registered: 2006-10-08
- Posts: 1,321
Re: My ghost zombie convergency theorem!
But they will never exactly overlap one another, won't they?
Offline
#5 2007-01-11 23:31:26
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: My ghost zombie convergency theorem!
That depends on how you look at it. The computer program will round the zombies' position data to a certain number of decimal places, so as there are a finite amount of positions each zombie can be at, there will eventually be a point where it would be impossible for 2 zombies to be closer to one another without being in the same space.
Also, if the victim stays still then they would all eventually reach him and stand in exactly the same place as him (and so, each other).
But you're right though, in all other cases, and if we're saying that distance is continuous, then they will never be in exactly the same place (although they will eventually become impossibly close to tell apart).
What would happen if for some reason, the zombies got confused and started going for each other? Zombie A --> Zombie B --> Zombie C --> Zombie A.
Or, perhaps even more confusing, what would happen if it was Zombie A --> Zombie B --> Zombie C --> you?
Why did the vector cross the road?
It wanted to be normal.
Offline
#6 2007-01-12 05:17:50
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My ghost zombie convergency theorem!
The possibilities are endless! ![]()
But yeah, they approach eachothers locations as a limit. But if the poor victim runs like mad for eternity, they're locations will be equal. Or infinitely close together.
Do you think my proof is adequet? I proved the distance between then is always decreasing but i didn't really proove it is bounded by zero. Untuitively, if you reach zero then your locations are equal and from there your paths are the same.
Think the proof is good enough or does it need a few more things?
Those are some cool ideas, mathsy. I may need to check them out. I think in A chasing B chasing C chasing A would be a triangle that continued to shrink and rotate.

I thought perhaps that new triangle would be similar to the first but turns out its not. Using similar reasoning, if we had lots of zombies, they would chase eachother in a shrinking circle. But again, ultimately their locations converge. Kooky, huh?
Last edited by mikau (2007-01-12 06:39:13)
A logarithm is just a misspelled algorithm.
Offline
#7 2007-01-12 05:32:22
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: My ghost zombie convergency theorem!
I think it's good enough. I certainly believe it is correct, because I can understand it perfectly and it matches with intuition and evidence, but I wouldn't know if it's actually rigorous enough to be a proper formal proof. Ricky would probably know.
Incidentally, I was looking at the animation you posted, and I can see that the method of control for the victim is to move a mouse around the screen that he follows. I realised that a more intelligent set of zombies would follow the mouse pointer instead of the victim, and because of the proof you just posted, they would always get him!
Why did the vector cross the road?
It wanted to be normal.
Offline
#8 2007-01-12 05:43:22
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My ghost zombie convergency theorem!
EEEK! don't tell the zombies that!
As far as your other situation, with A chasing b chasing C chasing you, this brings to mind another idea which ought to be made into a theorem.
Now for this problem we're assuming everything is moving at the same speed.
If zombie A is chasing zombie B, the shortest distance between two points is the line that connects them. Therefore zombie A is taken the quickest route to zombie B. Unless zombie B runs directly away from zombie B, indefinately, then sooner or later zombie B will be caught. If zombie B is moving in varying directions and not fleeing its persuer, then ulimately its going to be caught.
This means that if zombie A is chasing zombie B, and zombie B is chasing zombie C and zombie C is chasing you, zombie A will catch B, since B is only concerned with catching C and is not avoiding A in the required fashion. And thus B will catch C. Finally, all of them will catch you unless you are continuously running away from C. But if you are fleeing C in random directions, then ultimately they all end up together and have the victim for dinner!
This is fun...
Last edited by mikau (2007-01-12 06:18:35)
A logarithm is just a misspelled algorithm.
Offline
#9 2007-01-12 07:56:01
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: My ghost zombie convergency theorem!
Ah, but as you can indirectly control the movements of C, because C always follows you, then that means that you might be able to move in such a way that C is always moving away from B. Possibly. Certainly going in the same direction forever would work, but I'm not sure if it can be done in a finite space.
I agree that if the victim is concerned about purely running away from C, then A, B and C would eventually meet. But could a clever victim run away from C whilst also keeping C away from B (and if they're really clever, B from A as well)?
Why did the vector cross the road?
It wanted to be normal.
Offline
#10 2007-01-12 09:35:17
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My ghost zombie convergency theorem!
I think if you were to run away from C in order to keep C away from B as you suggested, then you would soon be caught by C as you were only concerned with keeping C away from B, not from yourself.
They only way what your suggesting could happen, that I can think of, is if they are all lined up in a row, all running along the same line. Because the theorem doesn't apply there.
Also, if the victim stays still then they would all eventually reach him and stand in exactly the same place as him (and so, each other).
ah, but doesn't the theorem only state they will converge to the same point and follow the same path? They obviously converge to the same point and there paths are all to stand still.
Last edited by mikau (2007-01-12 10:05:58)
A logarithm is just a misspelled algorithm.
Offline
#11 2007-01-12 10:18:37
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My ghost zombie convergency theorem!
I may have just found a flaw in the theorem here. Technically the distance between them is always decreasing but that doesn't necessarily mean they will appraoch zero. One side of the right triangle is approaching zero but the other side remains unchanged. The distance between them will approach the length of that vertical side. If the victim keeps changing his course they will converge ultimately. But if the victim continues to run in a straight line, the persuers tend to get behind him. (especially if the victim is a bit faster then the zombies which is usually the case.) When that occurs the angle between their paths approaches zero and thats when the theorem does not apply.
Hmmm... perhaps a bit more thinking to do. But still ultimately their paths are exactly alike, but their locations may not be. Perhaps the theorem should stipulate that the victim does not flee in a constant direction.
Last edited by mikau (2007-01-12 10:25:02)
A logarithm is just a misspelled algorithm.
Offline
#12 2007-01-13 05:46:41
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: My ghost zombie convergency theorem!
Because you posted that animation as an example, that implied that we were talking about a finite space where the victim and zombies could go. If that was the case, then it would be impossible for the victim to keep running in the same direction anyway. (Unless the game has asteroid-style warpy walls, but then there's the added complication that the zombies could suddenly end up in front of you.)
Why did the vector cross the road?
It wanted to be normal.
Offline
#13 2007-01-13 07:02:14
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My ghost zombie convergency theorem!
hehehe!
So yeah we could make the stipulation that they are enclosed in a finite plane. (and not a globe)
Still I think the theorem needs a little redefining.
A logarithm is just a misspelled algorithm.
Offline
#14 2007-01-13 09:03:57
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: My ghost zombie convergency theorem!
The animation got me thinking about the days I played world of warcraft ![]() In there I would take advantage of the very behavior of the mobs you're describing. Here's how it went: I was playing a mage. Mages have various spells which does a fixed, though varying, amount of damage to mobs in a certain radius. These are called AoE's(Area of Effect), and, as you might have noticed already, they can come in handy when the mobs are able to stand at the same spot. You'd just make some monsters, the more the better, run after you - and then run in circles 'til they were standing tight. After that, it was just hitting your AoE spells
In there I would take advantage of the very behavior of the mobs you're describing. Here's how it went: I was playing a mage. Mages have various spells which does a fixed, though varying, amount of damage to mobs in a certain radius. These are called AoE's(Area of Effect), and, as you might have noticed already, they can come in handy when the mobs are able to stand at the same spot. You'd just make some monsters, the more the better, run after you - and then run in circles 'til they were standing tight. After that, it was just hitting your AoE spells ![]()
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
#15 2007-01-13 09:34:52
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: My ghost zombie convergency theorem!
Mmm, this comes in handy with most games where hordes of enemies all try to follow you. Just run around in circles for a while and you'll end up with effectively one enemy that takes a while to kill instead of the lots of easily killable enemies that you had before. Which makes the game a lot easier.
By the way, how can something be fixed and varying?
Why did the vector cross the road?
It wanted to be normal.
Offline
#16 2007-01-13 09:52:28
- Patrick
- Real Member

- Registered: 2006-02-24
- Posts: 1,005
Re: My ghost zombie convergency theorem!
yeah, I was going to explain what I meant, but forgot it. By fixed I meant that the damage dealt to a monster wasn't determined by a formula that looked like, or similar, to:
If it was, the method wouldn't be effective, becuase you could end up doing near 0 damage if enough monsters were gathered.
Varying is supposed to mean that, for example, the spell called Frost Nova does 34-40 damage instead of 37 all the time. This doesn't mean that all monsters get hit by the same amount though. Say there are 5 monsters, then the following could be a possible event:
Monster #1 recieves 34 damage
Monster #2 recieves 37 damage
Monster #3 recieves 40 damage
Monster #4 recieves 38 damage
Monster #5 resists
Another important note, regarding this method, is that the mana you use per spell doesn't scale with the amount of monsters.
Support MathsIsFun.com by clicking on the banners.
What music do I listen to? Clicky click
Offline
Pages: 1