Math Is Fun Forum

rosana

Member

Registered: 2006-04-18

Posts: 4

The Conway Polynomial

hi,
How are you ?
I want any information , any topic ,website or any definition can help me to understand and explain these searching ( THE CONWAY POLYNOMIAL for louis H.Kauffman )because I do not understand it

thank you for your help

Moved to Help Me! - Ricky

Devantè

Real Member

Registered: 2006-07-14

Posts: 6,400

Re: The Conway Polynomial

Here's a good explanation from Wolfram's MathWorld: http://mathworld.wolfram.com/ConwayPolynomial.html

Zhylliolom

Real Member

Registered: 2005-09-05

Posts: 412

Re: The Conway Polynomial

I realize the poster is probably long gone by now, but I am in a knot theory class currently and might as well post some content in this thread. I can try to give more knot theory formulas if there is any request (it doesn't seem like a hugely popular field, however).

The Conway Polynomial

The Conway polynomial is a polynomial invariant of knots and links described by the following three axioms:

Axiom 1: For each oriented knot or link K there is an associated polynomial ∇[sub]K[/sub](z) ∈ Z[z] (Z[z] is the ring of polynomials in z with integer coefficients). If one knot K is ambient isotopic to another knot K' ( K ~ K'), then ∇[sub]K[/sub] = ∇[sub]K'[/sub].

Axiom 2: If K is ambient isotopic to the unknot (K ~ O), then ∇[sub]K[/sub] = 1.

Axiom 3: Suppose that three knots or links K[sub]+[/sub], K[sub]-[/sub], and L differ at one crossing in the manner shown below:

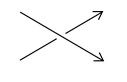K[sub]+[/sub]
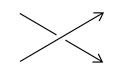K[sub]-[/sub]
L

Then ∇[sub]K+[/sub] - ∇[sub]K-[/sub] = z∇[sub]L[/sub].

Axiom 1 tells us that for any knot or link there exists a Conway polynomial; Axioms 2 and 3 give us a way to find it. Tomorrow I shall post an example of how to use these axioms to find the Conway polynomial of a knot (using a specific example, most likely the trefoil, but maybe some others), and perhaps I shall also describe the Jones polynomial, the HOMFLY polynomial, the chromatic polynomial, and more.

Edit: Wow, sorry about that, I could have sworn this topic had been replied to very recently, and I didn't realize it had been moved from the formulas section.

Last edited by Zhylliolom (2007-02-20 20:45:06)