Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2006-10-26 08:45:26
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
derivative of inverse secant function d (sec^-1(x))/dx
getting pretty confused here. We know since trig functions are always repetitious, we must restric our output to a certain range when creating an inverse function. But supposedly not everyone agree's on the restricted range for the inverse secant function. Some say the range should be [0, pi/2) and [pi, 3/2pi) others say it should [0, pi/2) and (pi/2, pi]. Ok... but this two definitions have different derivitives.
Below is a graph of x as a function of y x = sec (x)

to make this into a function we use the first range restriction: [0, pi/2) and
[pi, 3/2pi) 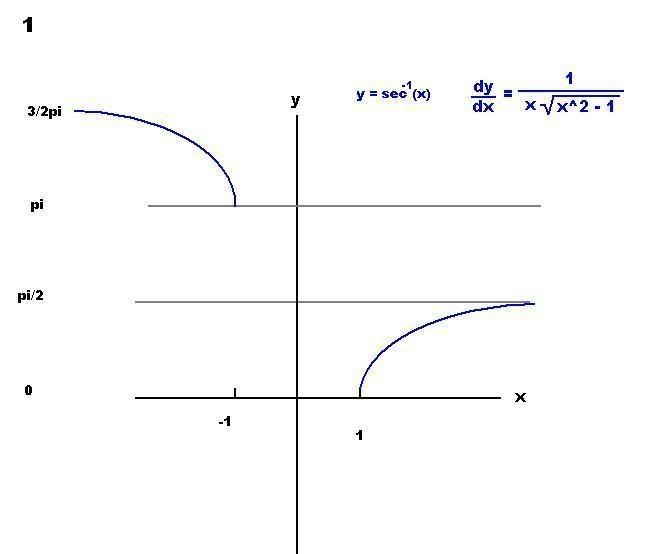
Now using the alternate definition where the range restriction is [0, pi/2) and (pi/2, pi] we have:
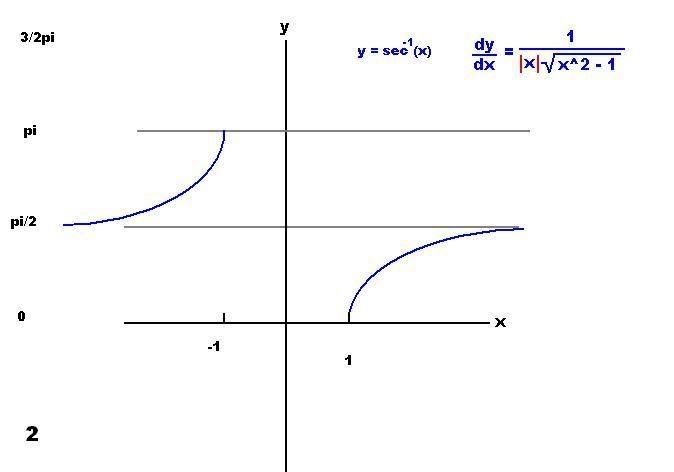
Note the derivatives. It makes sense the second derivative contains the absolute value term since we can see from the graph the slope is always postive, but how would we figure that out without graphing?
To calculate the derivaties, we have y = sec^-1(x) so sec (y) = x differentiating implicitly we get dy/dx = 1/(sec y tan y) now here's where I start to get uncomfortable. We know sec(y) = x and must be x. But if we say tan(y) = sqrt( 1 - sec(y)) or tan y = sqrt ( 1 -x^2) we are really finding |tan(y)| therefore when tan (y) < 0 the derivative should be incorrect. So why isn't it?
In the second equation we have to replace sec(y) with |x|. How come? y ranges between 0 to pi/2 or 0 to 90 in which case the secant IS positive, but also from pi/2 to pi or 90 to 180 degree's, where the secant while be negative.
This is rather confusing...
Last edited by mikau (2006-10-26 09:10:20)
A logarithm is just a misspelled algorithm.
Offline
#2 2006-10-26 09:48:31
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: derivative of inverse secant function d (sec^-1(x))/dx
ay y i yi! I think I just figured it out but its not pretty... the derivative of sec u is not in fact sec u tan u, its sin u / sec^2 u Now it makes sense. Using this definition, between pi/2 to pi the sec(y) is negative but it's squared so its back to positive, sin(y) is positive from pi/2 to pi so the whole thing is positive. Since the whole expression sin y/sec^2 y is positive we can replace it with |sec(y)||tan(y)| which is |x|sqrt(1 - x^2) this explains why the slope is positive.
On the other hand, when we let y range from pi to 3/2pi or 180 to 270, then we have sin y / sec^2(y) and sec^2(y) is always positive but sin y is negative when y is between 180 and 270 degree's so the slope in this case is negative.
So in the first case, you can find that sin y / sec^2 y is equivilent to x sqrt(x^2 - 1) within the limits of the range, and in the second case sin y/sec^2 y is equivilent to |x| sqrt (x^2 - 1) within the limits of the range.
This is why I feel trigonometric identities are extremely dangerous. I'm always uncomfortable when using them...
Last edited by mikau (2006-10-26 09:54:22)
A logarithm is just a misspelled algorithm.
Offline