Math Is Fun Forum

Jai Ganesh

Administrator

Registered: 2005-06-28

Posts: 52,910

Centre of Gravity (Center of Gravity)

Centre of Gravity (Center of Gravity)

Gist

Center of gravity (CG) is the point within an object where its weight is evenly balanced in all directions. Understanding its significance is important because it helps predict how an object will behave when it's moved or supported.

The centre of gravity (CG) of an object is the point at which all of its weight is evenly distributed. It is also known as the centre of mass.

It is important to know the centre of gravity because it predicts the behaviour of a moving body when acted on by gravity. It is also useful in designing static structures such as buildings and bridges. In a uniform gravitational field, the centre of gravity is identical to the centre of mass.

Summary

A body's center of gravity is the point around which the resultant torque due to gravity forces vanishes. Where a gravity field can be considered to be uniform, the center of mass and the center of gravity will be the same. However, for satellites in orbit around a planet, in the absence of other torques being applied to a satellite, the slight variation (gradient) in gravitational field between the parts closer to and further from the planet (stronger and weaker gravity respectively) can lead to a torque that will tend to align the satellite such that its long axis is vertical. In such a case, it is important to make the distinction between the center of gravity and the mass center. Any horizontal offset between the two will result in an applied torque.

The mass center is a fixed property for a given rigid body (e.g., with no slosh or articulation), whereas the center of gravity may, in addition, depend upon its orientation in a non-uniform gravitational field. In the latter case, the center of gravity will always be located somewhat closer to the main attractive body as compared to the mass center, and thus will change its position in the body of interest as its orientation is changed.

In the study of the dynamics of aircraft, vehicles and vessels, forces and moments need to be resolved relative to the mass center. That is true independent of whether gravity itself is a consideration. Referring to the mass center as the center of gravity is something of a colloquialism, but it is in common usage and when gravity gradient effects are negligible, center of gravity and mass center are the same and are used interchangeably.

In physics the benefits of using the center of mass to model a mass distribution can be seen by considering the resultant of the gravity forces on a continuous body.

Details

The centre of gravity, in physics, is an imaginary point in a body of matter where, for convenience in certain calculations, the total weight of the body may be thought to be concentrated. The concept is sometimes useful in designing static structures (e.g., buildings and bridges) or in predicting the behaviour of a moving body when it is acted on by gravity.

In a uniform gravitational field the centre of gravity is identical to the centre of mass, a term preferred by physicists. The two do not always coincide, however. For example, the Moon’s centre of mass is very close to its geometric centre (it is not exact because the Moon is not a perfect uniform sphere), but its centre of gravity is slightly displaced toward Earth because of the stronger gravitational force on the Moon’s near side.

The location of a body’s centre of gravity may coincide with the geometric centre of the body, especially in a symmetrically shaped object composed of homogeneous material. An asymmetrical object composed of a variety of materials with different masses, however, is likely to have a centre of gravity located at some distance from its geometric centre. In some cases, such as hollow bodies or irregularly shaped objects, the centre of gravity (or centre of mass) may occur in space at a point external to the physical material—e.g., in the centre of a tennis ball or between the legs of a chair.

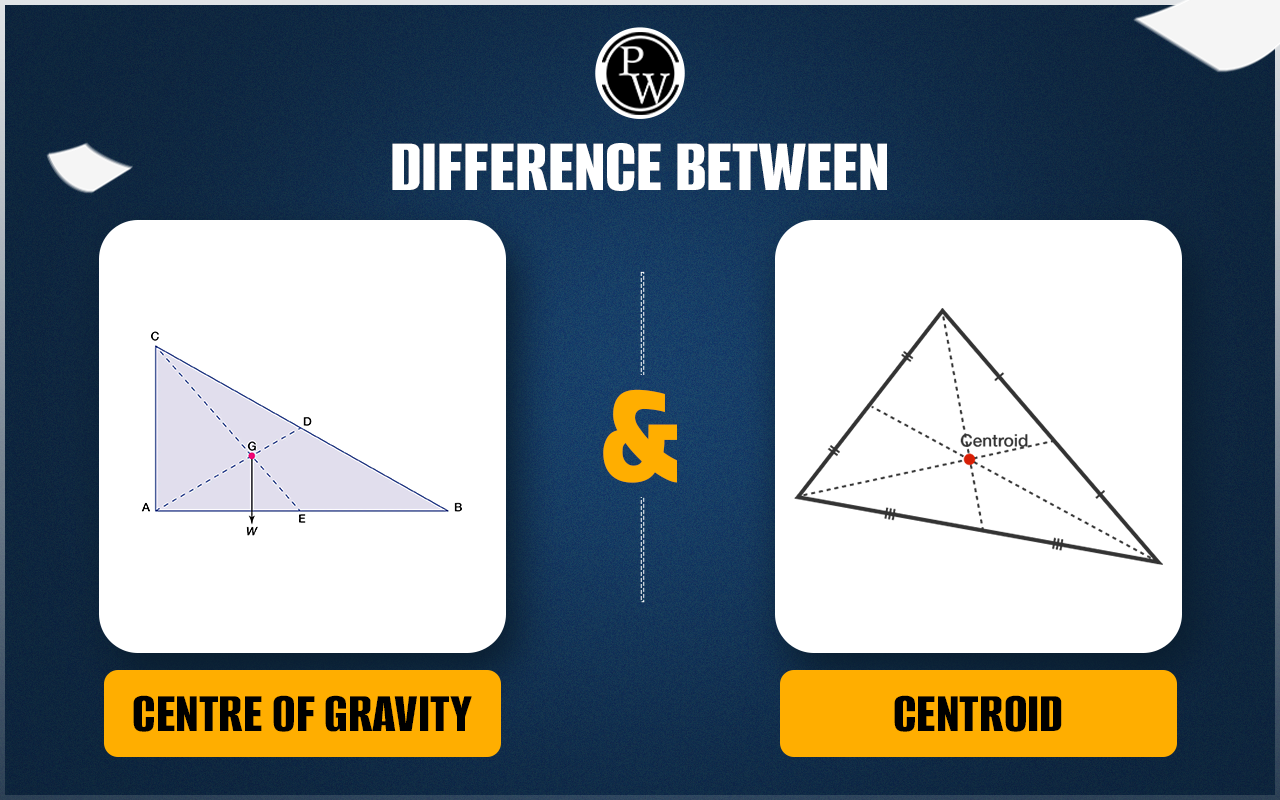
Published tables and handbooks list the centres of gravity for most common geometric shapes. For a triangular metal plate such as that depicted in the figure, the calculation would involve a summation of the moments of the weights of all the particles that make up the metal plate about point A. By equating this sum to the plate’s weight W, multiplied by the unknown distance from the centre of gravity G to AC, the position of G relative to AC can be determined. The summation of the moments can be obtained easily and precisely by means of integral calculus.

The centre of gravity of any body can also be determined by a simple physical procedure. For example, for the plate in the figure, the point G can be located by suspending the plate by a cord attached at point A and then by a cord attached at C. When the plate is suspended from A, the line AD is vertical; when it is suspended from C, the line CE is vertical. The centre of gravity is at the intersection of AD and CE. When an object is suspended from any single point, its centre of gravity lies directly beneath that point.

Additional Information

The center of gravity is a geometric property of any object. The center of gravity is the average location of the weight of an object. We can completely describe the motion of any object through space in terms of the translation of the center of gravity of the object from one place to another, and the rotation of the object about its center of gravity if it is free to rotate. If the object is confined to rotate about some other point, like a hinge, we can still describe its motion. In flight, both airplanes and rockets rotate about their centers of gravity. A kite, on the other hand, rotates about the bridle point. But the trim of a kite still depends on the location of the center of gravity relative to the bridle point, because for every object the weight always acts through the center of gravity.

Determining the center of gravity is very important for any flying object. How do engineers determine the location of the center of gravity for an aircraft which they are designing?

In general, determining the center of gravity (cg) is a complicated procedure because the mass (and weight) may not be uniformly distributed throughout the object. The general case requires the use of calculus which we will discuss at the bottom of this page. If the mass is uniformly distributed, the problem is greatly simplified. If the object has a line (or plane) of symmetry, the cg lies on the line of symmetry. For a solid block of uniform material, the center of gravity is simply at the average location of the physical dimensions.

---

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.

Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.