Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2006-04-07 11:16:54
- gsandy
- Member
- Registered: 2006-04-07
- Posts: 4
Radius given arc length and central rise
Given the curved arc length and central rise (distance from centre of chord to centre of arch), how is the radius caculated? thanks Sandy:(:(
Offline
#2 2006-04-07 16:52:50
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,148
Re: Radius given arc length and central rise
The length of an arc of a circle is given by the formula
where r is the raidus of the circle.
But the question gives us only the distance from the centre of the chord to the centre of the arc. Let this length be l.
Lets assume the arc is formed by the two radii with an angle θ.
Let the distance from the centre of the circle to centre of the chord be x.
Let the arc cut the circle at points X and Y and O be the Centre.
Let the Centre of the chord be M and centre of the Arc be N.
MN=l, OM=x, ON=OM+ON = l+x
But ON=r, therefore, l+x=r.
An isoceles traingle XOY is formed.
The length of the chord is given by the formula
.
In triangle OMX, OX=r, OM=x=r-l and
From this the radius can be found (I guess
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#3 2006-04-07 17:22:06
- gsandy
- Member
- Registered: 2006-04-07
- Posts: 4
Re: Radius given arc length and central rise
Havnt quite solved the problem yet. Following you logic to the next step I get:
B/(1-cosB) = (arc length x 90)/(pi x rise): B is 1/2 arc bisect angle in degrees & rise is your OM (l)
Now need help to solve for B
Offline
#4 2006-04-07 22:33:48
- Jai Ganesh
- Administrator

- Registered: 2005-06-28
- Posts: 53,148
Re: Radius given arc length and central rise
gsandy,
You get two equations with two variables, r and θ. The simultaneous equations can be solved and r and θ can be found.
The first equation is
The arc length is given in the problem.
The other equation is
(By Pythagoras theorem)
where l is the distance from centre of chord to centre of arch. This is given in the problem. ![]()
It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.
Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.
Offline
#5 2006-04-08 05:18:32
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Radius given arc length and central rise
While we're on the subject, I derived a cool formula to find the radius of a circle when the length and height of the chord are found. Like so:
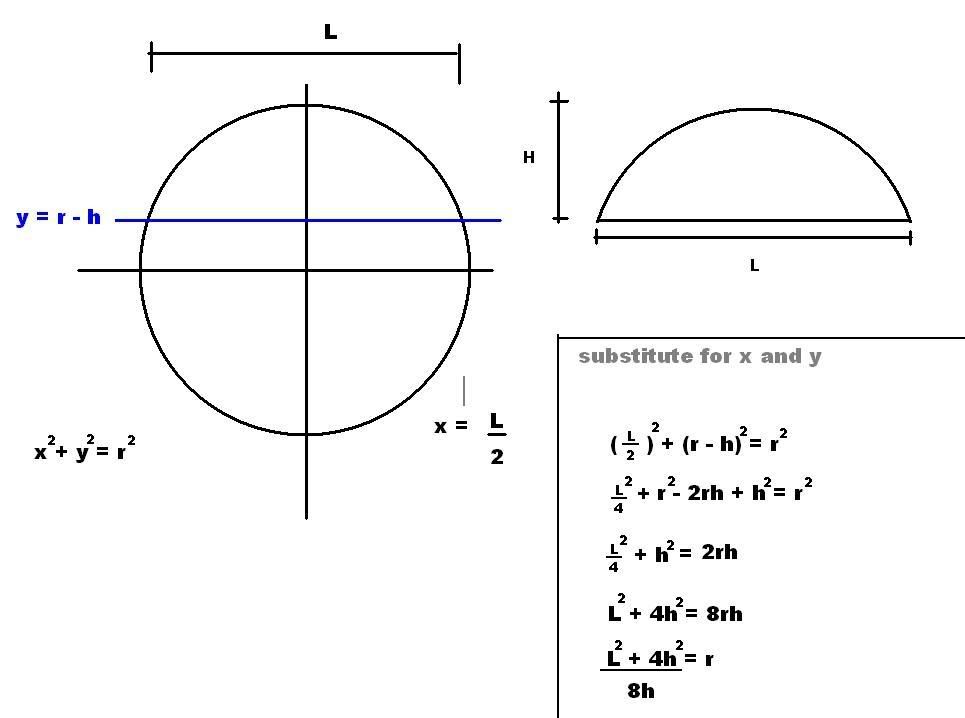
You simpy determine the intersection of the line y = r - h and x = L/2, substitue these values and rearranged. I was pleased to find the r^2 term is eliminated. And of course this formula can be rearanged to solve for either L or H if the two remaining values are known. I needed this to find the focal length of a spherical reflector I got, so I worked out this formula to solve it for me. Worked perfectly!
Ah the power of math...
Last edited by mikau (2006-04-08 05:31:47)
A logarithm is just a misspelled algorithm.
Offline
Pages: 1