Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2013-09-15 14:05:49
Magic Square
Given a set of numbers and the assurance that they can be put into a magic square, how can you put them into a magic square?
Last edited by Agnishom (2013-09-15 14:12:03)
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#2 2013-09-15 15:40:49
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
Odd or Even?
Odd are pretty easy.
For the numbers 1,2,3,...n^2
tried this and it worked on n = 3.
For even it is much more difficult. For singularly even ( n = 6,10,14... ) there is no known general formula.
For doubly even n = 4,8,12... there are methods given by both Chandru Ami and Dr. Mike.
There is a paper in the ACM for a general algorithm for all even by Collison but it is not free even though it was published in 1962 and the author is probably deceased. Sickening!
It is possible to download freeware to generate them and there is a new paper that is free but I have not read it yet.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2013-09-15 17:04:50
Re: Magic Square
These are the numbers:
11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#4 2013-09-15 17:07:45
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#5 2013-09-16 00:31:46
Re: Magic Square
How did you do this?
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#6 2013-09-16 01:03:16
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
I used a known one and plugged in your numbers.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#7 2013-09-16 01:39:22
Re: Magic Square
Known one?
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#8 2013-09-16 02:02:54
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
Hi;
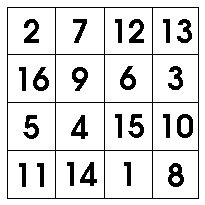
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#9 2013-09-16 02:17:03
Re: Magic Square
How are these two related? I am totally confused
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#10 2013-09-16 02:18:20
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
Take a look at the square in post #8 and add 10 to every box. What do you get?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#11 2013-09-16 02:23:26
Re: Magic Square
A box with all numbers from 11 to 26....perfect!
But you have shuffled them in post #4
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#12 2013-09-16 02:28:29
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
That is just a different 4 x 4 magic square. There are more than one.
Check the rows and columns and diagonals, each will be 74.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#13 2013-09-16 02:48:46
Re: Magic Square
Yes. Is there a way to figure out the magic number without sorting a square?
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#14 2013-09-16 02:54:00
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
There is a formula for the general ones. You would have to do some extra work for your type.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#15 2013-09-16 04:13:08
Re: Magic Square
For example?
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#16 2013-09-16 06:21:52
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,825
Re: Magic Square
Is there a way to figure out the magic number without sorting a square?
If there are n rows, the magic number must be
sum{all numbers}/n
The method I use is partly trial and improvement.
(i) Add up all the numbers. Divide by n to get the required total (=T) for any row.
(ii) Pick any set of n numbers that add to T. Make that row one.
(iii) Pick any set from the remainder that add to make T. Make that row two.
(iv) Continue like this until you have all the rows or an impossible set left.
(v) If the latter juggle some numbers about until the rows all work.
(vi) Now shuffle the numbers only within their rows until a column works too.
(vii) Keep that column fixed but shuffle the remainder within their rows until all the columns work.
(viii) Swap whole rows or whole columns until the diagonals work too.
example with 1,2,3,4,5,6,7,8,9
(i) sum = 45 => T = 45/3 = 15
(ii) I chose 9, 1, 5
(iii) Then I chose 7, 2 6 which meant the third row was bound to work as well: (iv)+ (v) 3,4,8 diagram one.
(vi) + (vii) see diagram two
(viii) The last two diagrams show whole row and column swaps.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#17 2013-09-16 06:44:34
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Magic Square
Hi;
In post #2 there is a formula for generating any odd n. You will be able to program it easily. I have also showed you how to modify them for your type of numbers, also easy to program.
For even n, as I said there is a new paper. But it is unrefereed and not even checked. It claims to have algorithm for all even n too. I have not verified their work.
Here is one that I did using M for the algorithm in post #2, it is a 15 x 15.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
Pages: 1