Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2006-02-03 15:12:52
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Volume as a function of height in sphere?
I'm stumped. I tried related rates, integrating cylindrical shells, and integrating using disks, all to no avail. Every method I try, leaves me in a total mess.
Everyone knows what the volume of a complete sphere is, but I am trying to find a function that will tell me the volume below a certain height from the bottom of the sphere. The familiar formula for the volume of a sphere is derived from integrating the function of a single quadrant from zero to the radius using the shell method and multiplying the result by two. But you cannot change the limits of integration to include values larger than R because the original function would then have to produce multiple values of y for a single value of x. Thus it no longer is a function.
I tried making two functions one for the upper bound and one for the lower, but again, after you pass R it becomes undefined. I'm lost. Any help would be greatly appreciated and the person who solves it would earn the rank of GOD in my opinion.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#2 2006-02-03 16:09:42
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
Are you talking about for instance, calculating the volume of water in a spherical container that is filled to a given height?
A logarithm is just a misspelled algorithm.
Offline
#3 2006-02-03 16:10:24
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: Volume as a function of height in sphere?
Exactly, mikau.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#4 2006-02-03 16:14:44
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
w00t! Very interesing. Have you considered integrating in terms of y using the pi r^2 method from y = 0 to y = h and adding that to the other half othe sphere? (unless the sphere is less then half full, but again a similar method might be doable.)
A logarithm is just a misspelled algorithm.
Offline
#5 2006-02-03 16:23:57
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: Volume as a function of height in sphere?
I never thought of mixing methods. But the disk method: ∫πf(y)²dy rotates about the x axis while the shell method ∫2πxf(x)dx rotates about the y axis. The two I would think are incompatible.
My last experiment was in trying to develop a function that changed with differing values of h, but still using x as the variable. It gave me a headache though, because you would have to reintegrate every time you wanted to use a different value of h.
I will keep playing with it, because this problem will probably haunt my dreams until I resolve it. Outwardly, it sounds very simple, but in practice.....
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#6 2006-02-03 16:24:47
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
This is what I mean.
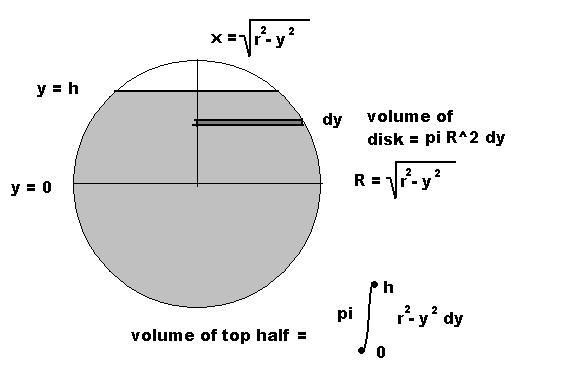
Last edited by mikau (2006-02-03 21:49:53)
A logarithm is just a misspelled algorithm.
Offline
#7 2006-02-03 16:41:09
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
But the disk method: ∫πf(y)²dy rotates about the x axis while the shell method ∫2πxf(x)dx rotates about the y axis. The two I would think are incompatible.
forgive me if I'm wrong but isn't the disk method integrated in terms of x when rotating about the x axis?
A logarithm is just a misspelled algorithm.
Offline
#8 2006-02-03 17:02:21
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: Volume as a function of height in sphere?
I don't know why I typed that. What I was trying to say was that the shell method revolves around the opposite axis of the variable while the disk method revolves around the same axis as the variable.
I might be doing something wrong but I integrated the function you have above and I got:
π [ ry - y³/3 ]
If r = 1 and h(upper) = 2 then this equals -2π/3
I'm not ripping, I liked your thought process too. It just doesn't seem to work in this instance.
edit!!
I didn't see that you were using the equator as the x axis.
Last edited by irspow (2006-02-03 17:05:23)
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#9 2006-02-03 17:27:40
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
woah! How could h be 2 if radius is 1?
A logarithm is just a misspelled algorithm.
Offline
#10 2006-02-03 18:49:09
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
oops! messed up there, its r^2 not just R. There we go!
A logarithm is just a misspelled algorithm.
Offline
#11 2006-02-03 21:43:39
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
If we work it out with the base of the sphere centered at the origin we don't have to worry about negative integrals, and can do it in one piece. If I integrate it for you...
Here you go! Volume as a function of height:
V(h) = pi ( r h^2 - 1/3 h^3) where r is the radius of the sphere and h is the height of the "water" measured from the bottom of the sphere. (ie. if the sphere were filled to the top, h = 2r)
Lets check. The formula for the volume of a sphere is 4/3 pi r^3, if radius is 1 the volume should be 4/3 pi. Now lets use my formula. if the sphere is filled with water the height of the water from the bottom of the sphere will be the diameter or 2r. The radius in this case is 1 so h is 2. Fill in these values and you get:
pi ( (1) (2)^2 - 1/3 (2)^3) = pi (4 - 8/3) = 4/3 pi same answer!
This time lets let h = 1. The volume will only be half. So it should come out to 2/3 π
pi ( (1) (1)^2 - 1/3 (1)^3) = pi( 1 - 1/3 ) = 2/3 pi. Again the correct answer!
It works! :-D This was fun!
Last edited by mikau (2006-02-03 21:53:16)
A logarithm is just a misspelled algorithm.
Offline
#12 2006-02-04 03:16:09
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: Volume as a function of height in sphere?
Nice, mikau, you have earned the rank of GOD in my opinion. I missed the substitution for R when I was going around in circles a few days ago. I kept seeing that x and, instead of substituting, I was banging my head trying to use related rates for x and y.
Once again, this forum has produced a neat little formula for all that have the pleasure of reading it.
Thanks again, mikau.
V(h) = πh²/3(3r - h).....sweeet!
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#13 2006-02-04 05:47:50
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
:-D No problem! But I have to decline the rank of "GOD". My real name, michael, means "who is like God?"
Of course if I'm an ancient greek god thats fine with me. Fear me...
A logarithm is just a misspelled algorithm.
Offline
#14 2006-02-04 06:05:44
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
And the wonderfull thing about calculus, now that we have the formula, differentiating allows us to calculate the rate at which the height is changing as the volume increases at a given rate and vice versa.
I love calculus....
And thanks for giving me such a fun problem. Solids of rotation are really awsome problems in my opinion.
Last edited by mikau (2006-02-04 06:14:12)
A logarithm is just a misspelled algorithm.
Offline
#15 2006-02-04 06:45:42
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: Volume as a function of height in sphere?
Yes, the concept of solids of revolution will always be etched in my mind. There was such a WOW factor to them in my mind when I was first introduced to them. I always find if amazing that many of the foundations for this type of computation were derived from individuals working by candlelight in an age which now seems eons ago. The imagination of the human mind is truly incredible.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#16 2006-02-04 06:49:20
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
Yeah, but whats most odd is no one can come up with anything new like that anymore. How come people were so much smarter a thousand years ago?
They just don't make geniuses like they used to.
One thing i'd like to know is how pi was discovered. And why the area of a circle is the integral of the circumfrence. WIERD!
Last edited by mikau (2006-02-04 06:56:26)
A logarithm is just a misspelled algorithm.
Offline
#17 2006-02-04 06:58:46
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: Volume as a function of height in sphere?
You must remember that people back then had very few alternatives to spending their time compared to what we now live like.
Take, in my opinion the greatest single contributors to mankind's knowledge, the Greeks for example. They created a slave system so that they could spend all of their time in "noble" pursuits such as the journey toward enlightenment. Euclid never "worked" a day in his life. All he ever had to do was contemplate new ways to view form and mathematics. In fact, "working" was regarded as dishonorable for a long period of their civilization, as it was viewed as a waste of human potential to understand truth.
Maybe sometime in the near future we will have the technology to take care of the mundane aspects of existence so that we too can focus our energy into mental and spiritual pursuits.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#18 2006-02-04 07:11:17
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Volume as a function of height in sphere?
Also they didn't have idiot boxes back then. Now people waste all their time staring slack jawed at some chicks bottom in high def.
A logarithm is just a misspelled algorithm.
Offline
#19 2006-02-04 15:29:20
- Tigeree
- Member

- Registered: 2005-11-19
- Posts: 13,883
Re: Volume as a function of height in sphere?
idiot boxes ? ![]()
People don't notice whether it's winter or summer when they're happy.
~ Anton Chekhov
Cheer up, emo kid.
Offline
#20 2006-02-04 16:00:23
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: Volume as a function of height in sphere?
Televisions.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
Pages: 1