Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2013-03-18 06:26:40
- genericname
- Member
- Registered: 2012-05-16
- Posts: 52
Proof by induction question
Hi, I am stuck on the last step. What am I supposed to do now?
Problem: Let T(n)=3T(n-1)+2, T(1)=2. Prove by induction that T(n)=3^(n-1)
Here is what I have so far:
Show base case k=1: T(1) = 3^1 - 1 = 2
Show for k=n-1: T(n-1) = (3^((n-1)-1)) -1
Show for k=n :
3((3^(n-2)) - 1) + 2
Last edited by genericname (2013-03-18 06:30:38)
Offline
#2 2013-03-18 06:57:34
- stapel
- Member
- Registered: 2006-07-22
- Posts: 15
Re: Proof by induction question
Hi, I am stuck on the last step. What am I supposed to do now?
Problem: Let T(n)=3T(n-1)+2, T(1)=2. Prove by induction that T(n)=3^(n-1)
Here is what I have so far:
Show base case k=1: T(1) = 3^1 - 1 = 2
If T(1) = 2 and if the proposed formula is as you've posted, then T(n) for n = 1 is 3^(1-1) = 3^(0) = 1, not 2. So the base step fails.
You appear, in your work, to have used a different formula from that which was proposed. Is there perhaps a typo somewhere? ![]()
Offline
#3 2013-03-18 06:58:42
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Proof by induction question
hi genericname
k=1
But you want T(1) = 2 ???
Let's see what is happening here.
term to term rule:
so if T(1) = 2
T(2) = 3x2 + 2 = 8
T(3) = 3x8 + 2 = 26
T(4) = 3x26 + 2 = 80
........................
So did you mean
Try again k=1
That's better.
Now for the induction step
assume
use the term to term rule
This has the right form, so the induction step is complete.
Bob
Last edited by Bob (2013-03-18 07:03:25)
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#4 2013-03-18 07:29:27
- genericname
- Member
- Registered: 2012-05-16
- Posts: 52
Re: Proof by induction question
Oops, it was a typo. Sorry! It was supposed to be (3^n)-1 like what Bob said.
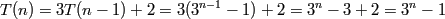
How did you get rid of the n-1 in that step?
Last edited by genericname (2013-03-18 07:29:47)
Offline
#5 2013-03-18 09:20:13
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Proof by induction question
It's just a matter of multiplying out the bracket( by 3)
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#6 2013-03-18 16:38:32
- genericname
- Member
- Registered: 2012-05-16
- Posts: 52
Re: Proof by induction question
Multiplying out the bracket? Sorry, think I might be misunderstanding something, but wouldn't that be (9^(n-1)) - 3 + 2 if you multiply by 3?
Last edited by genericname (2013-03-18 16:45:17)
Offline
#7 2013-03-18 19:13:02
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Proof by induction question
If you times by another 3 you just increaase the power by 1 ie (n-1) becomes n.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#8 2013-03-19 03:16:51
- genericname
- Member
- Registered: 2012-05-16
- Posts: 52
Re: Proof by induction question
Oh, I see. Thank you, bob.
Offline
Pages: 1