Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2006-01-11 21:39:24
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Fundamental theorem of calculus explanation
The direct connection between the integral of a function and its area, I find mystifying. It seems more like a made up rule for a wierd game, but its true! How could it be that the graph of the function who's slope is represented by the current function at a given point, give us the area? How could the line tangent to a graph and area, two seemingly unrelated topics be so directly connected?
There are proofs but most of them usually involve manipulations and application of other theorems which in the end, proves it mathematicly, but doesn't really help us to see WHY it is so.
Pondering over the relations between velocity and position, I've noticed theres an easy way to demonstrate why it is so, which is relativly easy to understand. (but bear in mind you cannot be mathematical idiot to understand this demonstration)
Refer to the following diagram:
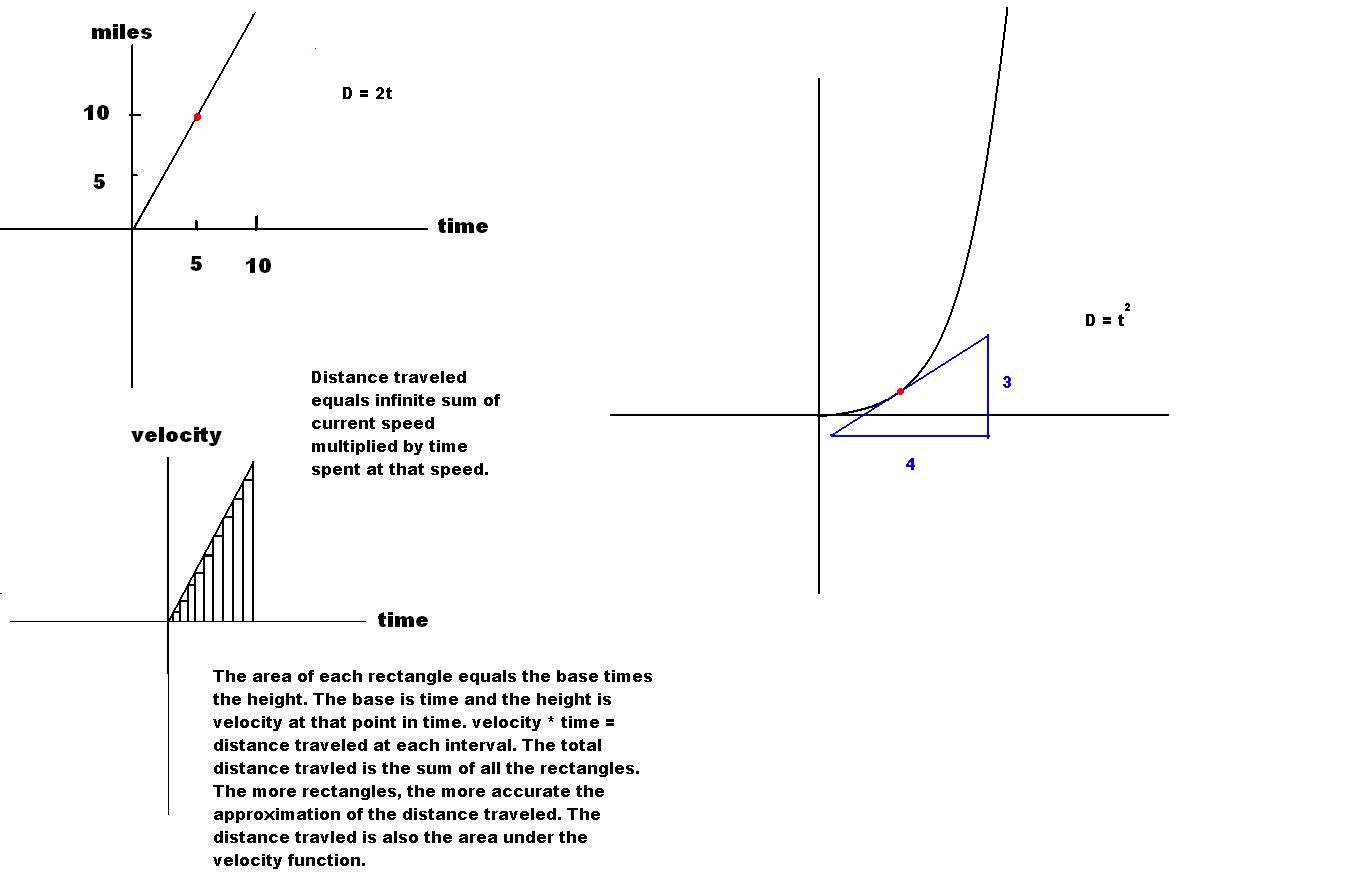
Lets say a car is traveling such that its position is defined by the straight line on the top left. The miles traveled is graphed vertically, and the hours driving is graphed horizontally. It appears the car drove 10 miles in 5 hours. rate * time = distance so rate = distance/time. He traveled 10 miles in 5 hours so his rate was 2 miles per hour. (Now thats a slow car!) Notice how 2 appears to be the slope of the graph!
Now take the graph on the right. In this graph, the distance traveled begins to accelerate upward, so it looks like the car is getting faster. So how fast is the car going at a certain point? Well the speed is constantly changing, but the speed at an individual point can be found, by observing the slope of the line at that particular point. Say for instance the car is at the location of the red dot. The distance he travels (the vertical height) divided by the time it took (the horizontal distance) is his speed at that point, because speed is distance traveled divided by the time it took. At this exact point his speed appears to be about 3 miles per 4 hours. Or if you reduce it, 0.75 miles per hour. NOTE! This does not mean he travled 0.75 miles in one hour, or 3 miles in 4 hours, it simply means his SPEED at that PRECISE location is 0.75 miles an hour, for a SPLIT second.
Hence, if you have a function describing how far you've traveled at a given time, the slope of the function at a given point in time, represents your speed at that point. The derivative of a function is the slope of the line at a given point, and thus, the derivative of a position function of time, is the speed at that given point in time.
Take a moment to be sure you understand why this is.
Now that we have demonstrated the derivative of position equals speed, we can work backwards.
If you are traveling 5 miles an hour, for 10 hours, you will travel 50 miles. Rate * time = distance. If you travel 3 miles an hour for 2 hours, 5 miles an hour for 2 hours, and 6 miles an hour for 2 hours, you will have travelled (3*2 + 5*2 + 6*2) miles, for a total of 28 miles. We see that if the speed is not kept at a constant, the distance traveled equals the sum of the the speed traveled at a particular time, multiplied by the time spent traveling at that speed.
Likewise, if your speed is smoothly increasing, how far you travel is an infinite sum of the speed at a given point multiplied by the time spent traveling at that speed. If you add up all the products of the rate at each infinitly short portion of time, multiplied by the time spent at that speed, at each infinitly small point in time, we will get the total distance traveled. Take a look at the bottom left diagram with the little rectangles. The area of each of these rectangles is the time spent on each short interval, times the height at that particular point in time. The sum of these rectangles approximates the distance traveled. The more rectangles we make, the more accurate the approximation. Notice that this also approximates the area under the velocity function, which also gets more accurate the more rectangles we use. Thus the distance traveled (on a given interval) equals the area under the velocity function. (on that interval)
The point I just made is not easy to explain in words (for me at least) hopefully this is easy for you to comprehend. If you simply can't understand this, then this explanation will not help you.
But we don't need to sum up an infinite number of rectangles who's heights are the current velocity at a given time, and who's bases are infinitly small portions of time. If we already have the position function, and we wanted to know how far the car will go in 5 hours, if the distance traveled by the car is given by D(t) = t^2 the car will travel 25 miles. (in 5 hours).
But what if we didn't have the position function? We have demonstrated that the derivative of a position function (where distance traveled is a function of time) gives us the speed at a given point in time. If speed is the derivative of the distance traveled function, then integrating the velocity (or speed) function, will give us the position, or distance traveled function.
So if we are given the velocity of a car equals 2t, this is the speed of the car at a given point in time. The velocity is the derivative of the position, (or "distance traveled") function. If we integrate we get position = t^2. At t = 5 the car will have traveled 25 miles.
But again recall, how the distance traveled equals the area under the curve of the velocity function (on a given interval). Thus if we wanted to know the area under the curve of the velocity function, we can integrate to find the position function. The distance traveled on a given interval equals an infinite sum of rectangles who's base is an infitly thin portion of time and who's height is the velocity at that point in time. This infinite number of rectangles is exactly the same as the area beneath the velocity function!
If we wanted to find the distance traveled between two points, for instance, how much distance you drove between the second and 5th hour, you always subtract initial position from final position to find the distance from one point to another, if you'd driven a total distance of 4 after two hours, and 25 after five hours, you drove a total of (25 - 4) or 21 miles between the 2nd and 5th hour. Again, distance traveled equals area under velocity function. So the area under the velocity function from a to b, equals the distance traveled at b minus the distance traveled at a. Distance traveled can be found by integrating velocity and the area under the velocity function (on a given interval) equals the distance traveled. So:
area under the velocity function on the interval [a, b] equals the integral of v(t) at t = b minus the integral of v(t) at t = a.
Those of you who see errors or innacuracies in this demonstration please point them out so I can correct them.
Last edited by mikau (2006-01-11 21:53:58)
A logarithm is just a misspelled algorithm.
Offline
#2 2006-01-13 14:20:12
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Fundamental theorem of calculus explanation
Nice explanations, mikau.
I've used these ideas myself to try to do problems on ILovePhysics.com, when I didn't know the formula.
igloo myrtilles fourmis
Offline
#3 2006-01-13 18:01:41
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Fundamental theorem of calculus explanation
WHEW! Someone made a comment! Thanks John E. Franklin. When no one says anything I think everyone hated it but is too polite to say so.
A logarithm is just a misspelled algorithm.
Offline
Pages: 1