Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2005-12-20 18:53:48
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Polynomial division, and more
John E franklin wanted to know about synthetic division, and the rational roots theorem. These are relatively simple so I thought I'd write up some explanations for all to see.
To divide a polynomial such as 2x^3 - 3x^2 + 5x - 7 by x + b, (where b is a constant) we can use traditional polynomial division. For those who don't know/remember how this works I wrote the following tutorial. Heres what we would do if we wanted to divide (2x^3 - 3x^2 + 5x - 7) by (x - 2):
Note! Close your "favorites" menu if you can't see the whole image"

Hope that helped. One thing I really should emphasize is both the divisor and the dividend MUST be written descending power of the variable!
For those who don't remember, this means terms containing variables come first, and those with the greatest exponents come first. The constant comes last. Thus 5x^3 -2x + 6x^5 +6 + 9x^4 - x^2 would be 6x^5 + 9x^4 + 5x^3 - x^2 - 2x + 6 when written in "descending power of the variable". This MUST be done first.
The other thing I should mention is if you wanted to divide a term like x^4 + 2x^2 + 3 by (x + 3). The dividend is already in descending power of the variable, but for polynomial division, it is necessary to to rewrite this as: x^4 + 0x^3 + 2x^2 + 0x + 3 and put this in the box. If you do the problem you will imediatly see why.
You may ask, what if I wanted to divide a polynomial such as (6x^5 + 9x^4 + 5x^3 - x^2 - 2x + 6 ) by binomial containing another variable, such as (x + y) or what if I wanted to divide by a trinomial, such as (x^2 + 3x - 5)? Well I have learned some more complicated polynomial division algorithms, but for this thread, I'm only going to discuss division by a binomial of the form (x + b).
I'll explain Synthetic division shortly. A symplified quicker version of polynomial division which is much faster. Then I will explain the remainder theorem, and the rational roots theorem. :-)
Last edited by mikau (2005-12-20 18:55:14)
A logarithm is just a misspelled algorithm.
Offline
#2 2005-12-20 19:59:55
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Polynomial division, and more
Ok now here's synthetic division.

The most important thing about synthetic division is to use -b in the box when you are dividing by (x + b) and + b in the box when you are dividing by x - b. Basicly when you are dividing by x - b you use b. So if you have x + b, you can rewrite it as x - (-b) and thus (-b) would go in the box.
So to divide by x + 3 use -3 in the box. To divide by x - 1 use 1 in the box. To divide by x - 8 use 8 in the box. To divide by x + 5 use 5 in the box and so on.
Sometimes some of the coefficients of synthetic division will come to zero. This is fine, just eliminate them when your done. It's still correct.
I'll get started on the remaindor theorem in a sec.
Last edited by mikau (2005-12-20 21:26:37)
A logarithm is just a misspelled algorithm.
Offline
#3 2005-12-20 21:16:50
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Polynomial division, and more
Hopefully I'll be able to do this without drawing lots of pictures.
The remaindor theorem.
Lets talk about remainders for a sec. Suppose you had 13 cookies and four kids. Being the wise parent that you are, you know one kid getting one extra cookie then the rest would start World War III. So you want each kid to get an equal number of cookies. But 13 will not divide evenly into 4. You consider cutting the remainders into 4th's with a knife, but they are crunchy cookies and would probably just crumbe. You could try to break them in fourths by hand but if they don't break 100% evenly, the war will start anyway. You decide to eat the remainder(s) yourself. If we use integer division which we all learned a gazillion years ago, finding how many cookies you get to eat is easy! 13/4, the answer is 3 with a remaindor of 1. (aw... you only get one cookie! >:-( ).
Now lets look at this again. What does this remainder represent? Well, if we separate the cookies into 4 groups of 3, 1 will be left The remainder. We had a 13 cookies in all and thus its obvious that 3 * 4 + 1 = 13.
But lets look at this yet again. We divided 13 by 4, got an answer of 3 with a remainder of 1.
13/4 = 3, Remainder: 1
Thus quotient * divisor + remaindor = dividend.
I use the term quotient loosely here. Technically its not a real quotient. Its an integer quotient.
When we learned fractions, we learned to put the remainder on top of the divisor to get an exact answer with no remainders. For situations when an object can be divided into parts of the whole.
Notice, with synthetic division we do the same thing. In the previous example, we got a remainder of 133. We wanted an exact answer so we placed 133 over (x + 2) to get an exact answer.
In algebra, we learned more clearly the direct connection between multiplication and division.
if x/y = 5 then x = 5 * y
Likewise, if:
(5x^4 - 6x^3 + 2x + 9)/ (x + 2) = 5x^3 - 16x^2 + 32x -62 + 133/(x+2)
then: (5x^4 - 6x^3 + 2x + 9) = (x + 2) (5x^3 - 16x^2 + 32x -62 + 133/(x+2))
But the expression on the left is the original polynomial thus we have rewritten the polynomail with a factor of (x + 2)
Remember how I said 133 was the remainder? We cut divided it by (x +2) to even it out, but what if we didn't?
If divide 13/4 and put the remainder over the divisor we get a remaindor of 1/4. But what if we didn't?
Remember earlier? 13/4 = 3 remainder 1. Thus 3 * 4 + 1 = 13.
Likewise (5x^4 - 6x^3 + 2x + 9)/ (x + 2) = 5x^3 - 16x^2 + 32x -62 Remainder 133
Thus (5x^3 - 16x^2 + 32x -62 )(x + 2) + 133 = (5x^4 - 6x^3 + 2x + 9).
But the expression on the left is the original expression. Therefore we've just rewritten it in a different form.
But lets take a look now, if we have the expression, (5x^3 - 16x^2 + 32x -62 )(x + 2) + 133, what value would it have if x = -2? well this would bring the the (x +2) factor to zero, and the whole expression in the parenthesis would have a coefficient of zero, and thus a value of zero. So what would be left? 133. The remainder.
Now lets think about what just happened. We divided the original expression by x + b using synthetic division and hence put -b in the box. The synthetic division allowed us to rewrite the expression into a form with x + b as a factor, and a remainder. (x+b)m + remainder = original expression.
When x has a value of -b, m has a coefficient of zero and no value and thus the expression has the value of the remainder.
Thefore, if we use synthetic division to devide a polynomail by x + b, then if we use -b as a value for x, the expression will have a value of the remaindor of synthetic division. But when we use synthetic division to divide by x + b, we put -b in the box.
THEREFORE! If you use synthetic division to divide a polynomial by placing b in the little box, the remaindor will be the value of the expression evaluated at b! This is the remaindor theorem.
I drew up a quick diagram to illustrate using synthetic division to quickly evaluate f(x) at x values of 3, -2, and 5.
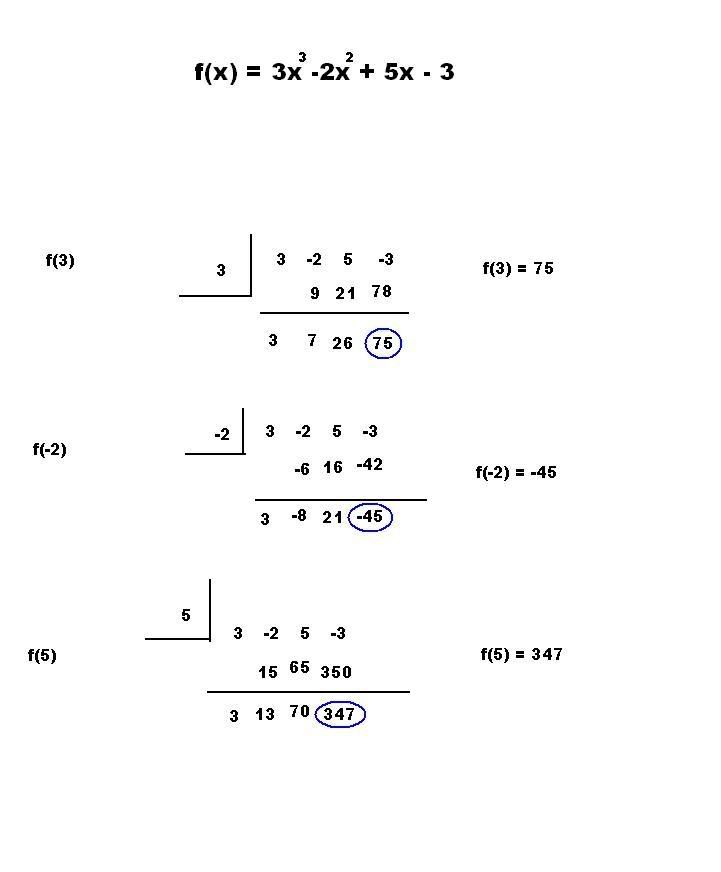
Last edited by mikau (2005-12-20 22:19:38)
A logarithm is just a misspelled algorithm.
Offline
#4 2005-12-20 21:54:01
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Polynomial division, and more
Ok, only one more thing to write about:
Rational roots theorem:
the coefficient of the term with the highest power in a polynomail is the leading coefficient.
ax^2 + bx + c
a is the leading coefficient.
5x^5 + 3x^2 + 9x^3 + 2
5 is the leading coefficient.
There will also always be a constant term in a polynomial. In the polynomial I just mentioned the constant was 2. In some cases there is no constant you could say the constant has a value of zero.
Anyways, I'll try to get right to the point. If a polynomial is written in the form of the equation, then the roots of the equation are those values for which the polynomial equals zero. Hence, you could use synthetic division of the polynomial, placing different values in the little box. If the remainder comes to zero, then you've found a value of x for which the expression has a value of zero, and you've found a root of the polynomial.
The rational roots theorem states, that if a polynomial has any rational roots (values of x that are integers or integer fractions that make the expression have a value of zero) these values can b found by looking at the leading coefficient (the coefficient of the highest degree term) and the constant at the end of the expression. They will give you clues.
The numerator of a root, will be an integral factor of the constant. The denominator of a root will be an integral factor of the leading coefficient.
Its best just to observe:
6x^3 + 2x + 5 = 0
Lets find at the integral factors of the constant 5:
5, 1, -5, -1
Lets find the integral factors of the leading coefficient:
6, 1, -6, -1, 3, 2, -3, -2
If this polynomail has any rational roots, then the root(s) is a/b where a is one of the factors of 5 (the constant) and b is one of the factors of 6 (the leading coefficient)
So if the polynomial has any rational roots then the roots are one or more of these:
1/6, -1/6, 1, -1, 5/6, -5/6, 1/3, -1/3, 1/2, -1/2
We don't know which of these, IF ANY are roots to the polynomail but we could use synthetic division with these values to quickly evaluate the polynomial at one of those values, and maybe get lucky and find one.
A logarithm is just a misspelled algorithm.
Offline
#5 2006-01-03 15:18:26
- God
- Member

- Registered: 2005-08-25
- Posts: 59
Re: Polynomial division, and more
While you're at it, here are some links to some other polynomial solving stuff...
http://mathworld.wolfram.com/DescartesSignRule.html
http://mathworld.wolfram.com/IntermediateValueTheorem.html
And for fun:
http://mathworld.wolfram.com/NewtonsMethod.html
This is horrible but helpful:
Last edited by God (2006-01-03 15:20:23)
Offline
#6 2006-01-03 18:29:49
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,711
Re: Polynomial division, and more
Mikau - you could you edit your posts, and use "Image Upload" like God did ... this way the image gets saved with the forum (in case photobucket stop serving the image).
You don't HAVE to, just an idea.
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#7 2006-01-03 18:50:28
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Polynomial division, and more
I'd love to! Saving to photobucket and copying it here is a real pain! But last couple times I tried that it didn't work. Let me try it again:
A logarithm is just a misspelled algorithm.
Offline
#8 2006-01-03 18:52:09
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Polynomial division, and more
Didn't work. Maybe I'm doing something wrong.
Last edited by mikau (2006-01-03 18:52:35)
A logarithm is just a misspelled algorithm.
Offline
#9 2006-01-04 00:17:09
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: Polynomial division, and more
No, you didn't do something wrong. Just the forum has limit to 1024x1024 pixels pictures.
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#10 2006-01-04 00:18:12
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: Polynomial division, and more
I wonder why Rod didn't think about that.
IPBLE: Increasing Performance By Lowering Expectations.
Offline
Pages: 1