Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#26 2005-11-06 11:54:26
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Here we are:

This is not an actual copy of an image produced by my program, (couldn't figure out a way to do that) just did my best to make a sketch. This is the kind of thing that tends to occur at certain angles. The box looks more like it is shapped like the black outline I drew on the right. The two top front corners appear to be leaning forward disproportionatly as if the front of the box is sloped. Other times the box looks like a paralellegram, and othertimes, it looks just fine.
So the investigation is under way.
A logarithm is just a misspelled algorithm.
Offline
#27 2005-11-06 12:48:30
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
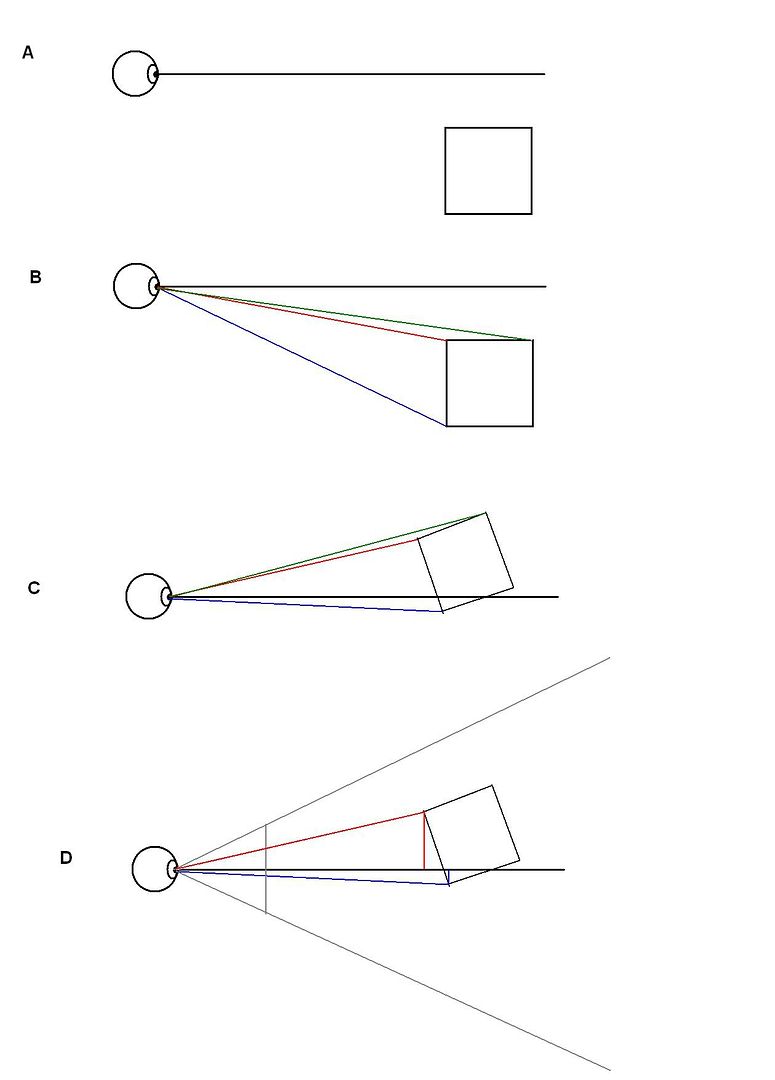
Ok heres a review of how the rotation and projection works. In this example we will only be finding the y coordinate of the point. Finding the x coordinate is the same only we work on the XZ plane rather then the YZ plane.
A. The location of the box on the YZ plane, Y being verticle, and Z horizontal.
B. The direct distance to each point from the viewers location (on the YZ plane) is measured. Using the distance formula sqrt((view.z - z)^2 + (view.y - y)^2) then the angle to the object on the YZ plane is measured in relation to the viewer using my polarangle function. We now have a distance and an angle of each point so we now know their polarform.
C. To rotate our viewpoint, we add the negative of the desired view rotation on the YZ plane to the angle of each points polar form. If a point was at sqrt (104) @ 45 degree's, and we wished to rotate our view 15 degree's down, we subtract 15 from the polarform. sqrt(104) @ 30 degrees. This will rotate every point down by 15 degree's as if we had rotated our viewpoint UP by 15 degrees. We then convert back to rectangular form for the new temporary coordinates of the object. This should work because when you rotate your view, the DIRECT distance from you to every point does not change, but the angle at which you see them does.
D. Now we use the simple projection scaler to scale every point down to the picture plane which represents the computer screen. These distances give us the y coordinates of where the point is to be displayed on the screen.
The same process is done on the XY plane to find the x coordinate.
Whats important is that both the horizontal and verticle rotations must be done BEFORE the projection is made. Because both rotations effect the z distance to the viewer, even though the DIRECT distance to the point is unchanging when you rotate your view.
It all seems correct, so why are some funny shapes showing up with certain angles of rotation and certain distances? I don't know, but I intend to find out. Is it a bug in my program? Or is the mathematical formula flawed in some way? One more possibility exists, viewing an object on a screen is slightly differant then looking at the world through a sheet of glass. I'll get into that in a second.
One thing I did to test the rotation engine, I used the 3d distance formula sqrt(x1-x2)^2 + (y1 - y2)^2 + (z1 - z2)^2) and checked the direct distance from the viewer to a point and had the value constantly being reevaluated and printed to the screen. As I rotated my view the directed distance did not change, as I moved the viewers location the distance changed. Everything working as it should there.
Ok while typing this I just found a new flaw. The object is first rotated on the YZplane and then on the XZplane. This works but they are done one at a time. After one rotation is complete, the next rotation is done horizontally, rotating the points as they were after the verticle rotation. This is like (for instance) looking downward, and then rotating your eyes to the left. If you rotate your eyes left after you rotated them down, then your eyes will begin to look towards your left and upwards, thanks to the vertical rotation. This is hard to explain in words so maybe I'll draw a picture. Anyway, this would result in slight rotations on the XY plane, as if the ground wasn't flat. With that in mind, some of the wierd shapes may actually make sense. I'll have to think for a bit on how to correct this.
A logarithm is just a misspelled algorithm.
Offline
#28 2005-11-06 13:54:39
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Well that might not be a flaw, I just rechecked my program and the XZ rotation is done first. Would it still occur? Seems like it wouldn't but these things tend to be unpredictable.
A logarithm is just a misspelled algorithm.
Offline
#29 2005-11-06 14:14:26
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Anyway, like I said, looking at a screen is differant in many ways from looking through a window. For instance, in a window, as you look though differant area's of the glass, your angle of view is changing. On a screen, your angle of view stays the same no matter where you look. Also when you look att a tv from a reasonably mild angle, your mind tends to correct it as if you were looking at it straight on. Which is why we can watch a movie without being normal to the screen, and it won't look messed up. So this is another differance. How your mind percieves the illusion of 3d on a 2d plane is much differant then where you see objects through a sheet of glass. So the mind may be trying to correct the image on a 2d plane and is actually distorting it. I often find that wierd distortions onscreen tend to not look so weird if I move my face closer to the screen.
Perhaps, my 60 degree viewing cone is simply too wide and requires to to be too close to the screen. If that be the case maybe I just need to shrink it a bit.
A logarithm is just a misspelled algorithm.
Offline
#30 2005-11-06 14:36:17
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
But I doubt thats it. Otherwise 3d images would be pretty demanding about where you sit and they aren't really.
The image looks fine with zero rotation. There must be some flaw with the rotation engine.
A logarithm is just a misspelled algorithm.
Offline
#31 2005-11-07 10:01:30
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Hmmmm to tell you the truth I'm not 100% sure there is something wrong. I just color coded the points and things seem to look better, perhaps I was just confusing the points of the front of the box and the back of the box.
A logarithm is just a misspelled algorithm.
Offline
#32 2005-11-07 18:29:37
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: My 3D engine: reinventing the wheel
As you know, there are some matrix manipulations that can "magically" do some of these things, but there can be a fair amount of number crunching. For example I had to give up on a proper animated torus in Flash, because I wanted to make it out of hundreds of flat surfaces (any less and it looked too chunky), but when the animation started it was too slow.
There is a possibility that your routines may perform faster, and that could make some those type of animations possible in Flash.
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#33 2005-11-08 08:52:43
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
I heard in 3d engines they look for matrices that either never change or change only once in a while and the program is designed to skip reevaluatlion when not necessary and use the result of the previous calculation.
A logarithm is just a misspelled algorithm.
Offline
#34 2005-11-11 00:39:37
- wcy
- Member
- Registered: 2005-08-04
- Posts: 117
Re: My 3D engine: reinventing the wheel
this is simply amazing.. try to make a 3d game!
Offline
#35 2005-11-12 11:09:49
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Thats the general idea but I immediately found I have a lot to learn about 3d linear algebra. Theres a book called "mathematics for 3d game programmers" which I intend to buy as soon as I finish calculus. I'll post more as I learn more. :-)
Btw, this engine still seems to have a few appearant bugs, I'm trying to work them out. So don't get too excited yet.
A logarithm is just a misspelled algorithm.
Offline
#36 2005-11-12 12:31:28
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Also, at this point, this just translates the locations of the points. They need to be connected with lines. This is easy as pi, mathematicly, but program-wise, finding a way to create new objects, and to quickly and efficiently connect them with lines to create a wire frame, and fill in the frames with color. Also programing each object which is a collection of multiple points connected with lines, to be a distinct object (for programming reasons) raises the complexity a bit.
There are also some things that must be implemented like "hiding" and object when it passes behind an opaque surface, also at least a primitive shading engine MUST be written, otherwise a red box could end up looking like a stop sign.
One thing at a time. But you can make a game with see though wire frame images, if you like.
A logarithm is just a misspelled algorithm.
Offline
#37 2005-11-12 19:19:41
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Hehehehheh! Well before I was using dots to plot the location of the corners but I found out, for some reason those dots were not coming out in the right spots. I was using small sprites as dots but when I started just drawing lines without sprites or dots, the new lines appeared in a slightly differant location and the box seems to look better now. On top of that I think I found out how to make screenshots so I may be able to post some shots now.
A logarithm is just a misspelled algorithm.
Offline
#38 2005-11-12 19:51:04
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: My 3D engine: reinventing the wheel
Looking forward to the screenshots. Use "Post reply" and then look for "Upload Slots" - the forum makes thumbnails etc.
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#39 2005-11-13 13:33:03
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Ok here we go.




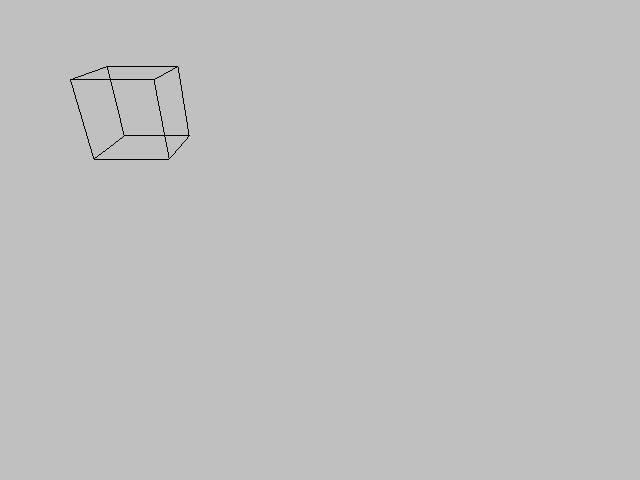
As you can see, some of them look somewhat odd, but I found the variables in these programs don't hold very accurate decimal numbers so this can only plot it so accurately.
A logarithm is just a misspelled algorithm.
Offline
#40 2005-11-13 13:59:49
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
What's somewhat peculiar is the wierd distortions that occur here and there seem to be consistant with the laws of perspective.
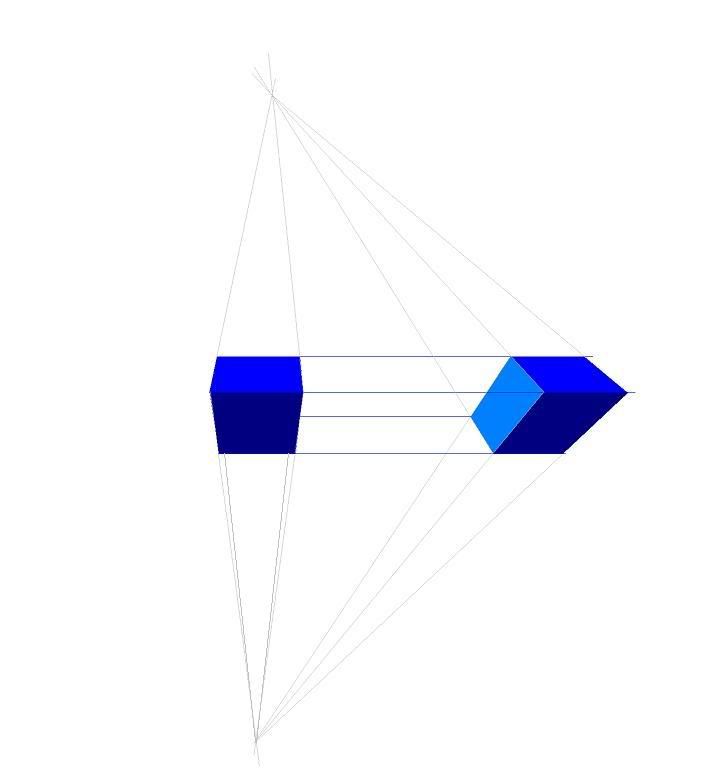
Take a look at this pic. When we look at the box with our angle of view tilted downward, the object appears to get wider as it moves up (since its getting closer to us) or you could just say its vanishing downward. If a box the same size is placed next to it, the same distance from you, and alligned parelell with the other box, all of the vanish points should be the same.
In this pic I drew a box pretty far to the right for an exagurated distortion. As you can see, the object is vanishing to the right points, but the box looks bizzare. Now this box is placed way too far out (the viewing cone should always be restricted to no more then 60 degree's) but like I said this is an exaguration to demonstrate a point.
Anyways, in the last two pics the view is tilted downward and the box is moved to the side. The same leaning occurs. The vanishing points are correct as my drawing demonstates. So, my math appears to be correct. Maybe I just need to keep the viewing cone moderately narrow.
A logarithm is just a misspelled algorithm.
Offline
#41 2005-11-13 15:24:21
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Hmmm... it would seem the problem with that is the vanish point is too close. If we wanted longer vanishing points, well everything would have to be smaller, and the image would need to be scalled up bigger. Take a look at this pic:
This the same box, only I moved the viewer inside it. The box now looks like its as big as a room and the vanishing points are much less abrupt. I think I read once that objects in 3d engines are supposed to vanish very slowly.
Anyways, if we were to use this box as the new room, the vanishing points are much less abrupt and we won't get that bizzare leaning distortion.
To do this, the size of the box would have to shrunk really small, and the scale factor would have to be increased to a very large number.
Of course, this throws off a lot of stuff, for instance a slight change of the viewers coordinates equals a big change in this, miniature world. So I'm really going to have to analyze this and see how everything is effected mathematicly by shrinking the objects size, and increasing the scalefactor. Then rearrange the formula into a more convenient form.
Now we're getting somewhere! :-D
A logarithm is just a misspelled algorithm.
Offline
#42 2005-11-13 15:47:19
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Hmmm... well I found out doing this is actually just restricting the viewing angle. Silly me.
But I still think the problem is definitly that they are vanishing too quickly. I'll need to think about this for a while.
Shrinking the objects and scalling up seems to fix the vanishing points but messes up the rotation. Perhaps if I redefined the rotation engine I could fix this.
A logarithm is just a misspelled algorithm.
Offline
#43 2005-11-13 16:23:54
- ryos
- Member

- Registered: 2005-08-04
- Posts: 394
Re: My 3D engine: reinventing the wheel
Hey mikau - did you ever get the rotation working? To be honest, I pretty much just worked out all that stuff I told you, and I haven't tested it (meaning I don't know if it works). I'd be interested to see if it has worked for you.
El que pega primero pega dos veces.
Offline
#44 2005-11-13 16:48:07
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
The rotation of a point about a line? Well I haven't had much time to work on it, as I've been working on the 3d engine. That question was actually for after I've got the 3d engine working fine, for use with doing character animations. To manipulate a characters limbs so I could rotate their limbs about their shoulders, elbows, etc, based on their current location. I will be looking into that as soon as I'm done getting this display system sorted out.
I do believe I have found a solution for the short vanishing points, I just need to get my thoughts organized. Will be posting as soon as I do. :-)
A logarithm is just a misspelled algorithm.
Offline
#45 2005-11-13 20:27:38
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
I think I've got it! :-)
Ok now this is pretty confusing so read carefully.
A. If we were to look at this 2 by 2 by 2 box from a distance of 12 units, the box would look reasonably small and the vanashing points would be pretty close. If we were to scale up the image size untill the box filled the screen, the vanishing points would be much further away.
B. If we wanted, we could "pretend" we were actually very close to the box instead of far away with a scaled up image.
C. So we're looking at the box from the location of the large head (the redline representing the screen) but we're "pretending" we're viewing it from the location of the small head.
D. But if we're "pretending" that we were as close to the box as I illustrated in B, if we were to rotate our view by about -30 degree's, we would expect to see the corner of the box in the center of the screen. But in reality, rotating our view by -30 degree's would result in that corner of the box being left of the center.
E. But, we insist on pretending we are that close, so instead, we rotate our real viewpoint about our pretend viewpoint. To make it look like feel like we're looking in our pretend direction by getting behind our pretend line of site. (kind of like operating a machine gun) continue below pic.
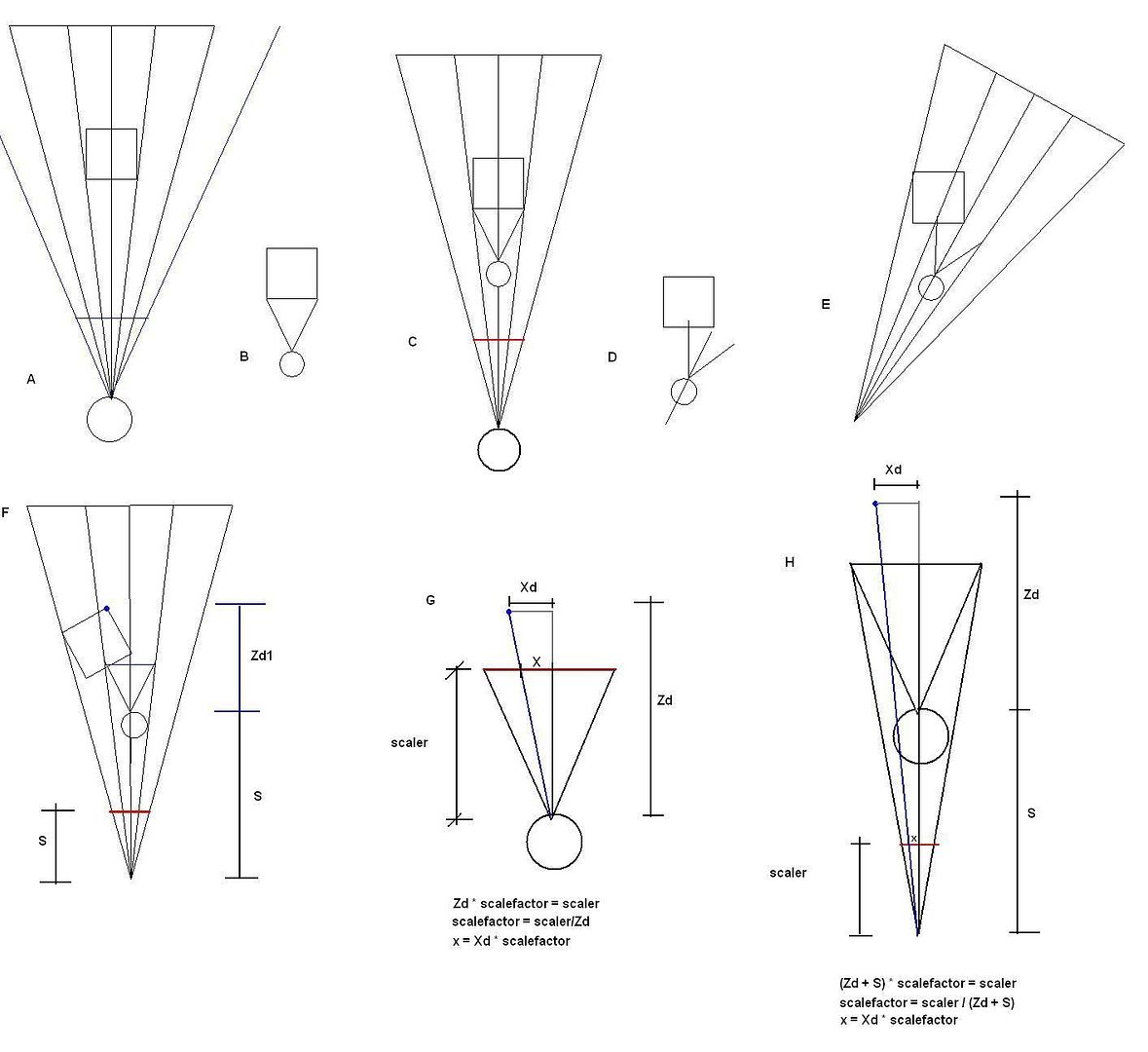
F. But if we rotate the entire picture back to vertical. We will find that the box has really just rotated around the viewer by + 30 degree's (the negative of -30), the same as it always does. So now all we have to do is scale it back to the screen. (the red line)
G. Originally, we found the coordinates of the virtual points using similar triangles. We checked the perpendicular distance from the viewer to the object, then drew two similar triangles. Then we find the scalefactor between the triangles. We then multiply the X distance from the viewer to the object, by the scale factor, to find the length of x. This gives us the x coordinate for where the object is to be displayed on the screen. (I used scaler as a variable, because increasing or decreasing its value, allows you to scale up or scale down the image.)
H. Now heres what it all comes down to. Our real viewing location is actually "S" units farther back then our pretend location. Now we want to scale the image down to the redline which is our screen. So the perpendicular to the point now equals the directed distance from the point to our pretend viewing location PLUS S. We now use (S + Zd) as the long side of the big triangle, and simply scale it down.
All I had to do was add the variable S to the Zdistance before scaling and change its value to adjust the extremity of the vanishing distances. Its a bit difficult to explain exactly why it does that, but its because zooming in makes the box larger and the vanishing points appear farther offscreen. We kind of mimiced the zoom effect by "pretending".
Pretending! A new mathematical concept!
Now I'll post some screens to show how well it works.
Last edited by mikau (2005-11-13 22:02:46)
A logarithm is just a misspelled algorithm.
Offline
#46 2005-11-13 20:58:46
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Here we are! :-D




Sometimes it takes you a second to understand what your looking at. Everything looks good doesn't it? If I ever feel like an object looks like its leaning a bit, like in the second from the top pic, I can fix it by increasing the value of S and scaling up the image. I have it set where I can increment and decrement their values with the keyboard, while the program is running so I can feel around for the right values. I'll toy around with it to find what values work best and eventually make them constant.
A logarithm is just a misspelled algorithm.
Offline
#47 2005-11-13 21:45:17
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
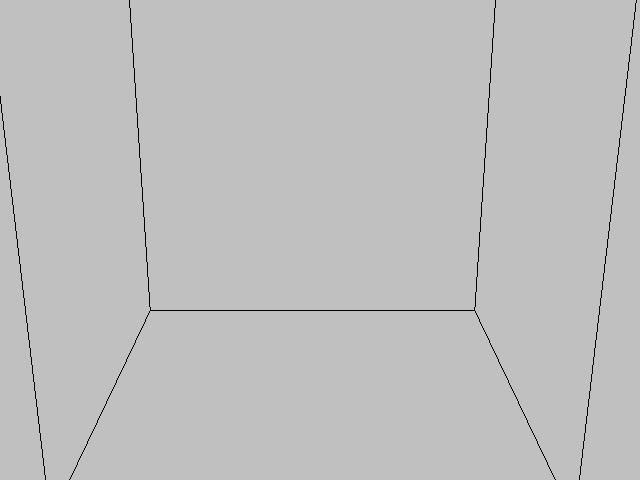
Some things to consider. Top left, At first I was treating the virtual observer, and the real observer as the same thing. This isn't necessarily incorrect but it produces vanishing points that are too short.
Top right. Instead we have the virtual observer (represented by the small circle) looking in one direction but the real obserer slighty behind that. Our angle is narrower but in relation to the virtual viewer, we can see things that would be way far out of his viewing cone. I understand now why in video games it always feels like everything is infront of us when it should far to the right or left of us. :-)
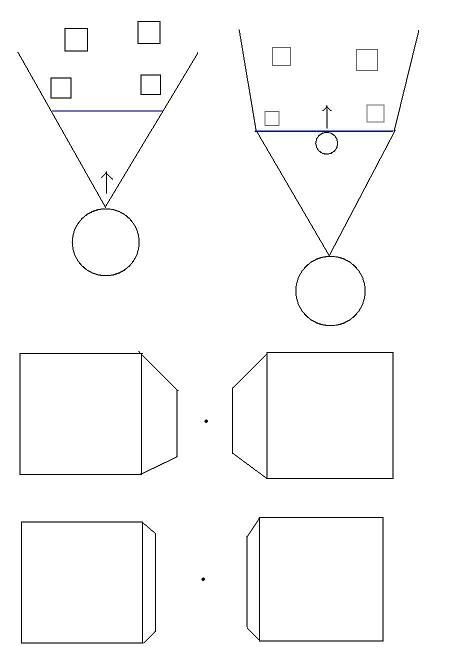
Heres another thing to consider. Bottom left and right pics. Vanishing points are the real meat and potato's of a 3d image. They create the illusion of depth, a third dimension. We needed to increase the distance of the vanishing points to avoid distortions. This is ok since it seems video games appear to do the same thing, but... if the vanishing point is close, we will see a lot of the insides of the two boxes (bottom left) but as the vanishing points get farther away, well, you see less and less of the insides of the box. (bottom right)
As the vanishing point gets farther away, our estimations of how close or far an object is, become more difficult to determine. For instance, in the bottom left, you can see a good deal of the side of the box and its pretty easy to estimate where the midpoint of that side is. On the bottom right, the exact location of the midpoint is more difficult to determine.
This gives me some idea's. For instance, if you wanted to make a video game, and their were certain times when greater depth perception would be helpfull (like in a fight) we could shorten the vanishing points, make the viewing cone more narrow (so we don't see the ugly distortions that quickly appear) and scale up the image a bit. This will give us a larger image, focused on a smaller area with enhanced depth perception. All your concern is your agressor so this would probably work great!
Anyways, thats all for now. :-)
A logarithm is just a misspelled algorithm.
Offline
#48 2005-11-19 17:46:24
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
You guys are about as talkative as I am in real life. (math is the only thing I can yap on about)
Anyways, the system I just invented is fine for third person games. (where you see your character) But is fundamentally flawed and would not work for first person games. When you rotate your view using this method, the actuall view is actually much farther behind then your pretend point of view, so you actually see things that should be behind you. If you program objects to dissapear if they go behind you, then objects disapear into an invisible wall instead of going off the sides of the screen.
The projection formula for plotting the points after the rotations are complete is this:
X = (Scalefactor * Xd)/Zd
Y = (Scalefactor * Yd)/Zd
Where Scalefactor is any desired constant, (which can be adjusted to zoom in or out) Zd is the measured distance from the viewer's z to the point's z on the z axis. Xd is the measured distance from the viewers x to the points x on the x axis. And Yd is the measured distance from the viewers y to the points y on the y axis. (crackers anyone?)
Most significant of those is the measured Z distance (Zd)
Zd = (point.z -viewer.z)
To shorten the vanishing points as I explained above, I added a constant C to this measurement to make everything C units farther away. It is important to note that short at long vanishing points follow the exact same line. BUT when the vanishing points are further back, objects stop vanishing quicker and appear to have less depth. See the pic of the four boxes I drew in the reply above? Both boxes vanish with 45 degree lines, but the boxes on the bottom appear to vanish slower.
So why do objects appear to vanish slower as they get farther away? Give me a sec I'll show you.
A logarithm is just a misspelled algorithm.
Offline
#49 2005-11-19 18:11:53
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: My 3D engine: reinventing the wheel
I read your posts ... like an unfolding novel. It is amazing how far you have come.
I just wish it was all in Flash (actionscript) so it could be shown live on the website. But Flash has relatively slow math compared to Java or C.
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#50 2005-11-20 12:12:44
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: My 3D engine: reinventing the wheel
Thanks. Sorry I was working on a thought and got an idea and stopped to test it. Didn't quite work but I might get it to work. I'll post more later. Busy busy!
A logarithm is just a misspelled algorithm.
Offline