Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2011-05-31 21:55:54
- bobcatfans
- Guest
Flaws in logic of solution to a couple of the logic problems
The solution given for the problem of the white and black marbles is flawed. We are dealing with combinations here and not permutations. Once a white marble is drawn, it doesn't matter if it was the first or second marble. There are only two possible outcomes at this point and therefore the probability is one in two.
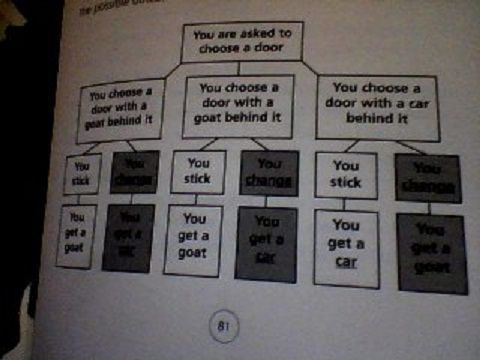
The solution for the problem of the goats and new car is similarly flawed. At the point that the one goat is shown, there are only two possibilities remaining. Changing your pick will NOT increase your probability of winning the car. The probability of your original pick DOES change once the one door is opened!
![]()
#2 2011-05-31 23:42:39
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Flaws in logic of solution to a couple of the logic problems
Hi bobcatfans;
Welcome to the forum.
If you are referring to the Monty Hall problem then switching is definitely favorable. Just tree the problem.
A long time ago Marilyn Vos Savant made a big stir when she caught a bunch of people making a mistake on this problem. The problem first pops up in a statistics journal circa 1958.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2011-06-13 20:58:15
- Anne Smith
- Guest
Re: Flaws in logic of solution to a couple of the logic problems
I quite agree with your last member. The options are only that it is a white or a black marble, because whether or not you have already selected marble 1 or two from bag A the next outcome is a white anyway.
#4 2011-06-13 21:29:30
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Flaws in logic of solution to a couple of the logic problems
Hi Anne Smith;
Welcome to the forum!
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#5 2011-06-14 00:32:19
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: Flaws in logic of solution to a couple of the logic problems
Are you referring to this: Bags of Marbles - Solution ?
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#6 2012-07-24 23:57:17
- Nicholas
- Guest
Re: Flaws in logic of solution to a couple of the logic problems
I agree this answer is wrong it says the answer is 2/3 because you are picking marbles not bags. That answer is if you were picking bags. The probability of you picking a white marble is 3/6 or simplified 1/2.
You have the wrong answer posted.
#7 2012-07-25 00:17:23
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,803
Re: Flaws in logic of solution to a couple of the logic problems
hi Nicholas,
Welcome to the forum!
Do you have a method for generating random events with known probabilities (eg. Excel) ?
If so, then try simulating this a large number of times. Maybe it will help to change your mind. ![]()
Or study Bayes Theorem and probability tree diagrams.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#8 2012-07-25 01:03:30
- anonimnystefy
- Real Member

- From: Harlan's World
- Registered: 2011-05-23
- Posts: 16,049
Re: Flaws in logic of solution to a couple of the logic problems
The problem is called Bertrand's box paradox.
There is another neat solution on wikipedia.
Here lies the reader who will never open this book. He is forever dead.
Taking a new step, uttering a new word, is what people fear most. ― Fyodor Dostoyevsky, Crime and Punishment
The knowledge of some things as a function of age is a delta function.
Offline
#9 2012-07-25 01:19:20
- noelevans
- Member
- Registered: 2012-07-20
- Posts: 236
Re: Flaws in logic of solution to a couple of the logic problems
Does the original problem state that the marbles are distinguishable or not?
Distinguishability makes a big difference in the way probabilities turn out. Could it be that the 1/2 comes from indistinguishability and the 2/3 from distinuishability? The solution in post #5 appears to assume distinguishability.
Some other important concerns in probability: Repetition vs not, replacement vs not, the sample space for the problem. ![]() Probability can be exceedingly tricky!
Probability can be exceedingly tricky!
Writing "pretty" math (two dimensional) is easier to read and grasp than LaTex (one dimensional).
LaTex is like painting on many strips of paper and then stacking them to see what picture they make.
Offline
#10 2012-07-25 01:32:19
- anonimnystefy
- Real Member

- From: Harlan's World
- Registered: 2011-05-23
- Posts: 16,049
Re: Flaws in logic of solution to a couple of the logic problems
I think the probability stays the same in both cases. Did you look at the Wikipeadia article on the Bertrand's box paradox.
Here lies the reader who will never open this book. He is forever dead.
Taking a new step, uttering a new word, is what people fear most. ― Fyodor Dostoyevsky, Crime and Punishment
The knowledge of some things as a function of age is a delta function.
Offline
#11 2012-07-25 06:25:33
- noelevans
- Member
- Registered: 2012-07-20
- Posts: 236
Re: Flaws in logic of solution to a couple of the logic problems
Yup! I looked at the Wiki article. But alas I haven't had time to really think about it all. I'm helping a friend move most of today.
Writing "pretty" math (two dimensional) is easier to read and grasp than LaTex (one dimensional).
LaTex is like painting on many strips of paper and then stacking them to see what picture they make.
Offline
#12 2013-10-22 20:01:06
- ILIA
- Guest
Re: Flaws in logic of solution to a couple of the logic problems
Do you have a method for generating random events with known probabilities (eg. Excel) ?
If so, then try simulating this a large number of times. Maybe it will help to change your mind.
Or study Bayes Theorem and probability tree diagrams.
Bob
Bob thank you for the pointer.
Regarding Monty Hall puzzle (3 doors 2 goats 1 car)
I tried using excel to make an experiment and almost convinced myself the 2/3 answer was right, but then I could not find the flaw in the alternative logic I was using:
Once the goat was revealed I am essentially asked to pick between 2 remaining doors with only one car between them. What makes one more likely than the other to contain the car?
I also tried applying Bayes' theorem:
Let's say I originally picked door 1 then door 2 was opened showing the goat so we want to calculate probability of car behind door 1 given that door 2 has a goat and probability of car behind door 3 given that door 2 has a goat.
Let's denote this P(c1|g2) and P(c3|g2)
Bayes' theorem: P(c1|g2)=P(g2|c1)*P(c1)/P(g2)
Given that door one has a car, door 2 must have a goat since there is only one car so P(g2|c1)=1
Given nothing (other than rules of the game) any door including door 2 has 2/3 goat chance so P(g2)=2/3
Given nothing (other than rules of the game) any door including door 1 has 1/3 car chance so P(c1)=1/3
P(c1|g2)=P(g2|c1)*P(c1)/P(g2)=1*(1/3)/(2/3)=1/2
Similarly P(c3/g2)=P(g2|c3)*P(c3)/P(g2)=1*(1/3)/(2/3)=1/2
As of now while I am not able to find a flaw in the logic that ends up with the answer 2/3 I also can't see any flaw with the logic above that ends up with 1/2 for an answer. Can you?
#13 2013-10-22 20:20:01
- ILIA
- Guest
Re: Flaws in logic of solution to a couple of the logic problems
Actually scratch that I think I do see the flaw in the official answer.
Let me first quote it:
"
Your first choice has a 1/3 chance of having the car, and that does not change.
The other two doors HAD a combined chance of 2/3, but now a Goat has been revealed behind one, all the 2/3 chance is with the other door.
"
The flaw is in the assumption that the 1/3 probability of car behind the door that you originally picked stays as 1/3 after the goat was revealed behind another door.
So let's say I picked door 1 but now door 2 opens and there is a car behind it would you still claim that probability of a car behind door 1 remained 1/3?
The first statement of the official answer is saying that P(c1)=P(c1|g2). Which is incorrect.
#14 2013-10-22 20:28:31
- anonimnystefy
- Real Member

- From: Harlan's World
- Registered: 2011-05-23
- Posts: 16,049
Re: Flaws in logic of solution to a couple of the logic problems
The problem is that door 2 might have a car behind it and not a goat.
Here lies the reader who will never open this book. He is forever dead.
Taking a new step, uttering a new word, is what people fear most. ― Fyodor Dostoyevsky, Crime and Punishment
The knowledge of some things as a function of age is a delta function.
Offline
#15 2013-10-22 22:08:25
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,803
Re: Flaws in logic of solution to a couple of the logic problems
hi ILIA
The game show host knows where the car is. When he/she reveals what is behind a door, this is not a random choice. It has to be a goat door and that's what makes all the difference.
If the first choice (1/3) was the car door, then either remaining door can be revealed, and the contestant will loose the car if a change is made.
But if the first choice was one of the goat doors (2/3) , then the host has to reveal the other goat and a change means a certain win of the car.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#16 2013-10-23 07:56:25
- ILIA
- Guest
Re: Flaws in logic of solution to a couple of the logic problems
Hi bob.
Thank you for your response, it is more convincing than the one in the official puzzle solution, but I am still unclear about where the flaw in my logic is.
I did know that the host didn't chose the door at random and I don't think I made any assumption about that in my logic.
#17 2013-10-23 08:06:11
- ILIA
- Guest
Re: Flaws in logic of solution to a couple of the logic problems
Correction: I do see that I made the assumption about host's random choice when I argued that if he revealed a car ...
That was me arguing for the flaw in the official answer - not a good argument.
But I do not see a flaw in my argument for the "alternative" answer (my first post). Do you?
#18 2013-10-23 08:12:05
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Flaws in logic of solution to a couple of the logic problems
Hi;
The first time I saw this problem is when it appeared in Parade magazine which was printed in Vegas on a Sunday. It pitted alleged super genius Marilyn Vos Savant against several mathematicians. Marilyn said switch and here is why:
http://marilynvossavant.com/game-show-problem/
Neither side knew or maybe Marilyn did that this was published in a rather famous Statistics journal circa 1975. It contained Marilyn's proof.
When you tree this as she did and the statisticians before her did you will see she is right provided Monty knows where the car is.
http://en.wikipedia.org/wiki/Monty_Hall_problem
The role of Monty is underestimated by many. Even the great Paul Erdos could not believe the answer!
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#19 2013-10-23 08:55:40
- anonimnystefy
- Real Member

- From: Harlan's World
- Registered: 2011-05-23
- Posts: 16,049
Re: Flaws in logic of solution to a couple of the logic problems
Even the great Paul Erdos could not believe the answer!
I cannot blame him. It is very counter-intuitive!
Here lies the reader who will never open this book. He is forever dead.
Taking a new step, uttering a new word, is what people fear most. ― Fyodor Dostoyevsky, Crime and Punishment
The knowledge of some things as a function of age is a delta function.
Offline
#20 2013-10-23 15:36:01
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Flaws in logic of solution to a couple of the logic problems
I got it wrong too, proving that bobbym = Paul Erdos. That was all I needed to convince myself that I belonged in math. After all, if I could get the same wrong answer as him I must be great too? I began to search for other probability problems that I could get wrong and lo, I found them.
Anyway, it is too bad that no one remembers the movie "Let's Make Love" with Yves Montand and Marilyn Monroe. In it Marilyn sings the "Specialization" number. How does this relate to anything in particular you might ask? I am glad you asked that question, you see when I saw how easily Marilyn Vos Savant did the problem by treeing it I changed the wording of the song to Computation, computation, you'll rule the barnyard if you compute, whoo hoo hoo hoo.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#21 2013-10-24 08:52:18
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,803
Re: Flaws in logic of solution to a couple of the logic problems
hi ILIA
So what was wrong with your Bayes?
I think you have the order wrong:
(i) A door is picked.
(ii) The host reveals a goat behind another door.
So let's say you pick a door.
Case one: P(it has a car) = 1/3
Now the host has to reveal a goat. That's easy because both remaining doors have goats, let's call them G1 and G2
P(G1 given car) = 1/2 ..... P (G2 given car) = 1/2
So if you choose to switch you will lose with P = 1/3 x 1/2 + 1/3 x 1/2 = 1/6 + 1/6 = 1/3
Case two: P(it has a goat) = 2/3
Now the host has no choice; he must reveal the remaining goat P(goat given goat) = 1
So if you choose to switch you win with P = 2/3 x 1 = 2/3
Bob
ps. I prefer tree diagrams to Bayes as it is easier to see what is happening without specialist knowledge and tree diagrams are much more versatile (you can have many events and more than two outcomes at each stage).
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#23 2013-10-25 03:18:03
Re: Flaws in logic of solution to a couple of the logic problems
Hi Nehushtan;
That is my favorite book but I do not have that diagram?! Did Chris speak about it?
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline
#24 2013-10-25 03:22:18
- Nehushtan
- Member

- Registered: 2013-03-09
- Posts: 957
Re: Flaws in logic of solution to a couple of the logic problems
Hi Agnishom.
Your edition of the book is probably different from mine; mine was published by Vintage. In that chapter of the novel, the narrator proved the Monty Hall problem in two ways: using the tree diagram, and by Bayess theorem.
240 books currently added on Goodreads
Offline
#25 2013-10-25 19:41:11
Re: Flaws in logic of solution to a couple of the logic problems
Hi bobcatfans;
The problem seems to be counter-intuitive to me too. Though I understand the Monte Hall, this version is harder.
However, now since the immediate requirement is to know who is right and who is wrong, we need to resort to some bobbym philosophy, i.e, experimental verification.
'And fun? If maths is fun, then getting a tooth extraction is fun. A viral infection is fun. Rabies shots are fun.'
'God exists because Mathematics is consistent, and the devil exists because we cannot prove it'
I'm not crazy, my mother had me tested.
Offline