Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2010-01-18 08:26:17
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
A silly prime number method.
Objective: Find prime numbers below 100, and the
non-prime or factorable numbers.
I'm going to use an exhaustive approach, that
finds each non-prime number once and only once
without getting double "hits".
You will see the flimsy algorithm unfold below
as utilizing combinations of factors in an
numerical way with the lowest primes being used
first.
Start with 2, and go up.
If multiply to over 100, then move on...
First just list the solely 2-factors: (2) 4 8 16 32 64 128
The next # is 3, and is prime since it is not above in list.
One 3-factor and zero-plus 2-factors: (3) 6 12 24 48 96 192
Two 3-factors and zero-plus 2-factors: 9 18 36 72 144
Three 3-factors and zero-plus 2-factors: 27 54 108
Four 3-factors and zero-plus 2-factors: 81 162
Next #4 is in list above, not prime, it is
4 = 2 times 2.
Next #5 is prime, not listed above.
One 5-factor and no 3-factors and zero-plus 2-factors: (5) 10 20 40 80 160
One 5-factor and one 3-factor and zero-plus 2-factors: 15 30 60 120
One 5-factor and two 3-factors and zero-plus 2-factors: 45 90 180
One 5-factor and three 3-factors and zero-plus 2-factors: 135 270
Two 5-factors and no 3-factors and zero-plus 2-factors: 25 50 100 200
Two 5-factors and one 3-factor and zero-plus 2-factors: 75 150
Two 5-factors and two 3-factors and zero-plus 2-factors: 225 450
Three 5-factors and and no 3-factors and zero-plus 2-factors: 125 250
The next # is 6, and is in a list above, so not prime,
6 = 3 times 2.
Next the #7 is not listed above so it is prime.
One 7-factor and no 5-factors and no 3-factors and zero-plus 2-factors: (7) 14 28 56 112
One 7-factor and no 5-factors and one 3-factor and zero-plus 2-factors: 21 42 84 168
One 7-factor and no 5-factors and two 3-factors and zero-plus 2-factors: 63 126
One 7-factor and no 5-factors and three 3-factors and zero-plus 2-factors: 189 378
One 7-factor and one 5-factor and no 3-factors and zero-plus 2-factors: 35 70 140
One 7-factor and one 5-factor and one 3-factor and zero-plus 2-factors: 105 210
Two 7-factors and no 5-factors and no 3-factors and zero-plus 2-factors: 49 98 196
Two 7-factors and no 5-factors and one 3-factor and zero-plus 2-factors: 147 294
Next # is 8 and it is in the list of 2-factors above, so it is not prime.
Then the # 9 is also listed above, so it is not prime, it is
3 times 3.
The # 10 is listed above, so it is not prime, it is
5 times 2.
Next 11 is prime as it is not listed above.
(Now I will abbreviate "factor" with just "f")
One 11-f and no 7-f and no 5-f and no 3-f and zero-plus 2-f: (11) 22 44 88 176
One 11-f and no 7-f and no 5-f and one 3-f and zero-plus 2-f: 33 66 132
One 11-f and no 7-f and no 5-f and two 3-f and zero-plus 2-f: 99 198
One 11-f and no 7-f and no 5-f and three 3-f and zero-plus 2-f: 297 594
One 11-f and no 7-f and one 5-f and no 3-f and zero-plus 2-f: 55 110
One 11-f and no 7-f and two 5-f and no 3-f and zero-plus 2-f: 275 550
One 11-f and one 7-f and no 5-f and no 3-f and zero-plus 2-f: 77 154
One 11-f and one 7-f and no 5-f and one 3-f and zero-plus 2-f: 231 462
(I am going a bit over 100 here just out of interest and curiosity)
One 11-f and one 7-f and one 5-f and no 3-f and zero-plus 2-f: 385 770
One 11-f and one 7-f and one 5-f and one 3-f and zero-plus 2-f: 1155 2310
Two 11-f and no 7-f and no 5-f and no 3-f and zero-plus 2-f: 121 242
Next is 12, which is listed above, so it is not prime, and is
3 times 2 times 2.
(I will abbreviate "zero-plus" with "zp" hereafter.)
Next # is 13, which is not listed above, so it is a prime number.
One 13-f and no 11-f and no 7-f and no 5-f and no 3-f and zp 2-f: (13) 26 52 104
One 13-f and no 11-f and no 7-f and no 5-f and one 3-f and zp 2-f: 39 78 156
(From hereon out I will not type the "no" quantities; wastes space)
One 13-f and one 5-f and zp 2-f: 65 130
One 13-f and one 7-f and zp 2-f: 91 182
One 13-f and one 11-f and zp 2-f: 143 286
Next # is 14, which is not a prime number as it is listed above.
The #'s 15 and 16 are not prime either as they are listed above.
The #17 is prime as it is not listed above.
One 17-f and zp 2-f: (17) 34 68 136
One 17-f and one 3-f and zp 2-f: 51 102
One 17-f and one 5-f and zp 2-f: 85 170
One 17-f and one 7-f and zp 2-f: 119 238
#18 is above listed.
The # 19 is prime, not above.
One 19-f and zp 2-f: (19) 38 76 152
One 19-f and one 3-f and zp 2-f: 57 114
One 19-f and one 5-f and zp 2-f: 95 190
One 19-f and one 7-f and zp 2-f: 133 266
Numbers 20, 21, and 22 are found above, so they are not prime.
The number 23 is prime and is not listed above.
One 23-f and zp 2-f: (23) 46 92 184
One 23-f and one 3-f and zp 2-f: 69 138
One 23-f and one 5-f and zp 2-f: 115 230
Numbers 24, 25, 26, 27, and 28 are found above, so are factorable and not prime.
The number 29 is the next prime and is not listed above.
One 29-f and zp 2-f: (29) 58 116
One 29-f and one 3-f and zp 2-f: 87 174
One 29-f and one 5-f and zp 2-f: 145 290
The number 30 is not prime as it is
found under the 5's section above.
The number 31 is prime as it is not above.
One 31-f and zp 2-f: (31) 62 124
One 31-f and one 3-f and zp 2-f: 93 186
One 31-f and one 5-f and zp 2-f: 155 310
The numbers 32, 33, 34, 35, and 36 are above so they are not prime.
The number 37 is prime as it is not above.
One 37-f and zp 2-f: (37) 74 148
One 37-f and 3-f and zp 2-f: 111 222
The numbers 38, 39, and 40 are found above, so they are not prime.
The number 41 is prime since it is not above.
One 41-f and zp 2-f: (41) 82 164
One 41-f and 3-f and zp 2-f: 123 246
The # 42 is found in the 7's section above so it is not prime.
The number 43 is not found above, even though 143 is, so 43 is prime.
One 43-f and zp 2-f: (43) 86 172
The #'s 44, 45, and 46 are not prime as they are above.
The # 47 is prime as it is not above.
One 47-f and zp 2-f: (47) 94 188
The numbers 48, 49, 50, 51, and 52 are listed above, so they are factorable,
or non-primes.
All the factorable non-prime numbers below 100 should be listed above
by now, as we are up to fifty, and we have been doubling everything!
So if you want to find a prime number between 50 and 100, just search
for it above, and if it is not found, it is prime.
Let's see if this is true. I'll list the ones not shown above.
I wrote all the numbers listed above that were between 50 and 100,
inclusive, and then found that 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97
were not listed above, so they are prime numbers. The numbers check
with some other internet sources, so that's good.
Last edited by John E. Franklin (2010-01-18 11:47:32)
igloo myrtilles fourmis
Offline
#2 2010-01-18 13:43:12
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
I've been reviewing print-outs of this, and the data structure "tree's" comes to mind when
filling out the non-prime tables in a reasonable order. The higher you get up the tree of
primes, then you have all the primes below it and itself for the sons and daughter member
branches for use in remultiplying. I'll work on a better algorithm soon as time permits and
try to explain it. "Tree's" are like structures in computer programming for things such as
hash sorts, etc.
igloo myrtilles fourmis
Offline
#3 2010-01-18 20:47:43
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: A silly prime number method.
I take it you have not heard of the sieve of Eratosthenes.
Offline
#4 2010-01-19 03:32:33
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
Actually, that's where I got the idea!! But with my way, you have to go to halfway, not the square root, so my
way is more work! And my way doesn't cross off all the even numbers first, just the powers of 2, so there are
differences. But you are right that they are basically the same in that we are crossing out the non-primes! When
I first learned about non-primes, I was very interested that the number of factors was so small.
igloo myrtilles fourmis
Offline
#5 2010-01-19 06:36:27
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
I guess the point of this exercise was to show you could go through
the non-primes using combinations such that you don't come up with
the same non-prime number twice or three times due to it's factors,
as with the Sieve method. But more than that, I am on a personal
mission to increase my awareness on the subject by doing, more than
by reading because I am a really poor reader.
igloo myrtilles fourmis
Offline
#6 2010-01-19 07:50:44
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A silly prime number method.
But with my way, you have to go to halfway, not the square root, so my way is more work!
I alone have the problem of long solutions. When someone comes up with a shorter demonstration than my own, I just scoff.
I am on a personal mission to increase my awareness on the subject by doing, more than by reading because I am a really poor reader.
I like the idea of doing, as I am a poor reader too. I read alot and come away with little.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#7 2010-01-19 08:45:59
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
Thanks for the comments bobby.
I think my next step will be to try to list all non-primes without
knowing the primes up to a 1000 on paper. But this time, I'm
going to do lots of things in parallel, and drop and pick them up
as my count increases. I think I might drop 2's and 3's because
you can tell those at a glance, due to even #'s or adding up the
digits. Just gotta find some really huge paper pad to start my
work on...
igloo myrtilles fourmis
Offline
#8 2010-01-19 09:32:37
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: A silly prime number method.
Just gotta find some really huge paper pad to start my work on...
As part of a fictitious biography:
One of his most important discoveries, still in use today, was that you can turn your paper sideways. This allowed mathematicians to work on even more complex formulas than they were previously capable.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#9 2010-01-19 10:02:09
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
Good one! Or go diagonally, as the work gets harder and easier, in an oscillatory pattern!
igloo myrtilles fourmis
Offline
#10 2010-01-19 13:15:12
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: A silly prime number method.
There was a good scene in "A Beautiful Mind" where JFN efficiently covered an entire blackboard. He even wrote inside the zeros!
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#11 2010-01-20 14:44:33
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
I've worked out the primes up to 500 by skipping products with 2, 3, or 5's in them, and just
starting with 7, 11, 13, 17, etc... Picking up and dropping data for reuse so far is not that hard.
I'll keep going towards 750 or 1000 tomorrow. I'm multiplying each time instead of adding so
I don't get any accumulative errors, just possible singular errors. Data checks with internet though!
It's interesting to me that Daniel Tammet knows all of these up to ten thousand by heart with
colors and feelings, and shapes, and light visualizations.
igloo myrtilles fourmis
Offline
#12 2010-01-21 10:12:25
- valona
- Member
- Registered: 2010-01-21
- Posts: 1
Re: A silly prime number method.
just go in diagonally,it gets easier
Offline
#13 2010-01-22 08:57:46
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
I'm up to 661 now. Diagonally? I'll keep that in mind.
igloo myrtilles fourmis
Offline
#14 2010-01-28 14:07:23
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
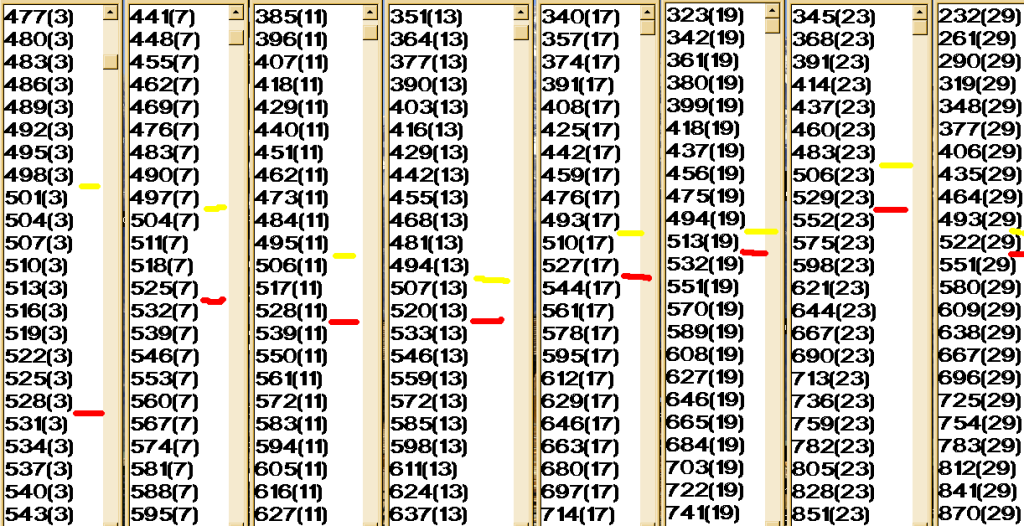
By using parallel multiplication tables, you can have a lot of
fun looking at the non-prime numbers!!!
It's not a waste of time just because the Sieve has already been done before.
Because the multiplication tables are very important.
Maybe someday we will discover more short-cuts for certain numbers if
we keep trying.
Here's a picture of several parallel multiplication tables centering
around the 500 to 530 mark. 500 yellow marker, 530 red marker.
The numbers in parenthesis are just there so you know what mult
table you are in fast.
igloo myrtilles fourmis
Offline
#15 2010-01-29 05:25:23
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
I have over 12 windows on my screen of columns of numbers now and
I just thought of something special Windows could do to the interface.
A button like the minimize button, except, the window simply goes behind
the other windows on the screen. If this exists, I'd love to know about
it, in any operating system. Anyone know.
Say you have Eight slim windows open like shown above in my
previous post, and then you have eight more on top of them.
Is there a way to make each window go behind as far as it can toward
the iconic desktop?? Even if it takes 8 quick clicks, that is fine, or
hot-keys (accelerators) ?
(The windows would remain "open", just go behind other windows...)
(That way, you could do the same to what came to the front when
the time was appropriate, and move it to the back of the screen)
(...kind of like a juggling act...)
Last edited by John E. Franklin (2010-01-29 05:36:29)
igloo myrtilles fourmis
Offline
#16 2010-01-29 14:23:40
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: A silly prime number method.
![]() (:
(:
igloo myrtilles fourmis
Offline
Pages: 1