Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2007-11-08 09:23:32
- tony123
- Member
- Registered: 2007-08-03
- Posts: 230
hexagon
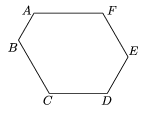
Each interior angle of the hexagon in the figure is 120°. Prove that
AB + FA = CD + DE.
Offline
#2 2007-11-09 23:24:40
- gyanshrestha
- Member
- Registered: 2007-11-06
- Posts: 41
Re: hexagon
if it is regular hexagon is posssible to prove. in that case all sides are equal and proof will easily follow.
if not the case then i think it is not possible.
sorry for inconvinience
http://gyan.talkacademy.com.np
Offline
#3 2007-11-09 23:32:34
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: hexagon
It does not have to be a regular hexagon. All Ive managed so far is to show that opposite sides must be parallel.
Offline
#4 2007-11-10 19:11:36
- gyanshrestha
- Member
- Registered: 2007-11-06
- Posts: 41
Re: hexagon
is it possible that opposite sides are parallel and their sum are equal?
then it must be BF=CE, then is it possible?
http://gyan.talkacademy.com.np
Offline
#5 2007-11-11 00:08:48
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: hexagon
No. Opposite sides do not have to be equal. The question is, prove that the sum of two adjacent sides is equal to the sum of the opposide two adjacent sides.
Offline
#6 2007-11-11 00:36:31
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: hexagon
This is another example of a hexagon with all interior angles equal to 120° but with sides of different lengths. Its been drawn to scale (hopefully) so you can print the image and measure its sides directly. (Presumably Tonys hexagon is also drawn to scale so you could also do the same thing with his polygon.)

Indeed, the result sum of adjacent sides = sum of opposite adjacent sides is true for all even-sided polygons (not just the hexagon) whose interior angles are all equal.
Last edited by JaneFairfax (2007-11-11 00:41:21)
Offline
#7 2007-11-16 09:28:41
- tony123
- Member
- Registered: 2007-08-03
- Posts: 230
Re: hexagon
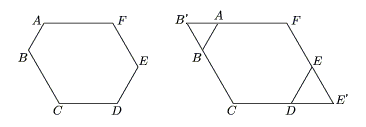
equilateral triangles at two opposite ends
Offline
#8 2007-11-16 09:37:33
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: hexagon
equilateral triangles at two opposite ends
Now that youve pointed it out

Offline