Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2007-08-16 09:55:19
- Manchild
- Guest
A hard question that popped up in the exams 8years ago!
...so the teacher says.
Three equal circles with radius r are drawn as shown, each with its centre on the circumference of the other two circles. A, B and C are the centres of the three circles. Prove that an expression for the area of the shaded region is:
A = r^2 / 2 (Pi - _/3)
I couldn't even start to attack the question ![]()
#2 2007-08-16 10:03:39
- Manchild
- Guest
Re: A hard question that popped up in the exams 8years ago!
Sh!!!!!!
Forgot to send an image of the circle....

#3 2007-08-16 10:05:41
- nsl22
- Member
- Registered: 2007-08-16
- Posts: 8
Re: A hard question that popped up in the exams 8years ago!
I don't see the image "drawn as shown". I know what it looks like, but do not know what the shaded region is.
Nevermind.
What is: "(Pi - _/3)"???
Last edited by nsl22 (2007-08-16 10:07:35)
Offline
#4 2007-08-16 10:26:57
- nsl22
- Member
- Registered: 2007-08-16
- Posts: 8
Re: A hard question that popped up in the exams 8years ago!
you could probably use this:
http://www.mathopenref.com/segmentarea.html
and this: http://www.mathopenref.com/arcsector.html
to come up with an answer.
Offline
#5 2007-08-16 11:32:11
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: A hard question that popped up in the exams 8years ago!
Consider the circle with centre A. The area of the sector bounded by the radii AB and AC and the arc BC (red area in diagram below) is
.This is also the area of the sector bounded by the radii BA and BC and the arc CA in the circle with centre B (blue area in diagram below) and that of the sector bounded by radii CB and CA and arc AB in circle with centre C (green area in diagram below).
Now add up all these areas. You get
. But this actually counts the area of triangle ABC three times. So we must subtract twice the area of the equilateral triangle ABC, which is .Hence the area of the shaded region is
.Last edited by JaneFairfax (2007-08-16 12:04:23)
Offline
#6 2007-08-16 11:58:48
- JaneFairfax
- Member

- Registered: 2007-02-23
- Posts: 6,868
Re: A hard question that popped up in the exams 8years ago!
Ive made three diagrams to illustrate what Im saying above.
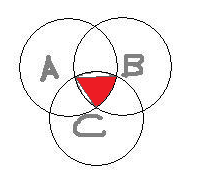
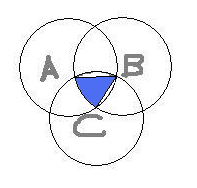
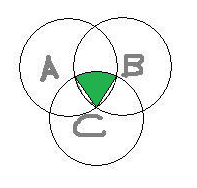
Offline
#7 2007-08-16 13:44:28
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: A hard question that popped up in the exams 8years ago!
Neatly done!
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#8 2014-02-08 07:13:15
- jesjesjesjes
- Member
- Registered: 2014-02-08
- Posts: 4
Re: A hard question that popped up in the exams 8years ago!
Hi, could someone explain why the area of each is
Last edited by jesjesjesjes (2014-02-08 07:13:37)
Offline
#9 2014-02-08 08:13:34
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,825
Re: A hard question that popped up in the exams 8years ago!
hi jesjesjesjes
Welcome to the forum.
The circles have equal radii, so the triangle formed by the three circle intersection points is equilateral, ie. has angles of 60.
The area of a whole circle would be pi r squared, and a 60 sector is 1/6 of this.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline