You are not logged in.
#1 2006-06-20 18:07:07
- tongzilla
- Member
Offline
Coin Problem
There are six identical coins with diameters a whole number of millimetres. I have started making a tray to stack them in, as shown:
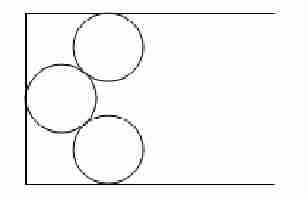
If I stacked the other three coins in the tray in a mirror image pattern of the first three, the smallest tray would be a two-figure number of millimetres wide. But if I repeated the above pattern, putting in a single coin next, then two on the right, the tray’s width could be reduced. In fact, it would be the same as before but with its two digits reversed.
What is the diameter of each coin?
Last edited by tongzilla (2006-06-21 01:43:42)
#3 2006-06-21 08:47:57
- MathsIsFun
- Administrator
Offline
Re: Coin Problem
Good puzzle, tongzilla. Possibly noone has solved it yet!
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
#4 2006-06-27 01:32:58
- tongzilla
- Member
Offline
Re: Coin Problem
Still no one?
I can only see one way of doing this problem, so I would be interested in what other methods can be used to work this out.
I will submit my solution once there is more discussion!
#9 2006-08-21 05:49:22
- mathsyperson
- Moderator
Offline
Re: Coin Problem
That is a very nice puzzle. I'd have tried to solve it earlier, but I've only just seen it because I was busy over the weekend. Anyway, I'm not entirely sure this is right, but here's what I've got:
And if that's not right then I'm well and truly stumped.
Why did the vector cross the road?
It wanted to be normal.
#10 2006-08-22 19:36:17
- tongzilla
- Member
Offline
Re: Coin Problem
mathsyperson, good work!
So which is your FINAL answer out of the two?
I will post my solution soon.
In the mean time, can you tell me what the overlap is given your coin diameters? That should give you a clue 
Last edited by tongzilla (2006-08-22 19:59:00)
#11 2006-08-22 23:49:48
- mathsyperson
- Moderator
Offline
Re: Coin Problem
Ooh, I get it.
Why did the vector cross the road?
It wanted to be normal.
#12 2006-08-23 13:29:52
- tongzilla
- Member
Offline
Re: Coin Problem
Good thinking mathsyperson! You're the winner of a matching salt and pepper set! In fact, there are other "solutions" that seem to fit, but if you examine the amount of overlap you will realise that it doesn't correspond to the diagram shown in the question.
#13 2006-09-05 04:52:19
- tt
- Member
Offline
Re: Coin Problem
Did you compare two coin orders (from left to right) of 1-2-2-1 with 1-2-1-2 or 1-2-2-1 with 2-1-1-2 , Mathsyperson ?
#14 2006-09-05 05:22:26
- mathsyperson
- Moderator
Offline
Re: Coin Problem
I started off with 1-2-2-1 and then switched the right-hand bit to get 1-2-1-2.
Why did the vector cross the road?
It wanted to be normal.
#15 2006-09-05 06:55:20
- tt
- Member
Offline
Re: Coin Problem
4d - 2o = 10a + b
4d - 3o = 10b + a ( a and b are arbitrary numbers between 1 and 9 inclusive)
Quite a lot of this cancels out, leaving o = 9(a-b).
(If o=9 then a-b=1, a>b; o<=d/2)
I came up with almost the same equations but yours are neater (using d instead of r) so I quote yours, hope you don't mind Mathsyperson.
I tried to cancel o out, leaving 4d=28a-17b
4d is even so 17b must be even or b even.
d, a, b are integers and d>0, a>0, b>0, a<>b
Replace a, b with value 1..9 or 2..8 and I have d=18; 8; 32; 46 mm
d=8 too small, d=46 too big a coin, that left d=18 mm (a=5, b=4) or 32 mm (a=7, b=4).
But it looks like only d=18 mm works.
What's wrong with my solution ?
Last edited by tt (2006-09-06 14:39:28)