Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2006-05-28 06:30:20
- lothy
- Member
- Registered: 2006-05-28
- Posts: 1
How do you find X?
Hello,
can anyone help me find X in this ecuation? n=x^x (x power of x), where n is given?
Does anyone know an algorithm for solving this?
Thanks for your time ![]()
Offline
#2 2006-05-28 14:11:17
- RickyOswaldIOW
- Member

- Registered: 2005-11-18
- Posts: 212
Re: How do you find X?
If you take an equation such as
2y = 4
and you wish to get the value of 'y', you must move the 2 over to the other side of the = sign.
We don't know the value of 'y' to start but we know that 2y equals 4. To get just 1y we must divide the 2y by 2:
2y / 2 = y
When you do somthing to one side of the equation you MUST do the same on the other side. Since we have divided the 'y' by 2, we must also divide the 4 on the other side by 2, so:
2y = 4
(2y)/2 = (4)/2
y = 2
_________________________________________________________________
With your example, we start with x^x. You wish to know the value of x. The opposite of to the power of is the root of. So to get x on its own we must:
x√(x^x) = x
We must again do this same step to the other side of the equation
n = x^x
x√n = x√(x^x)
x√n = x
Last edited by rickyoswaldiow (2006-05-28 14:44:20)
Aloha Nui means Goodbye.
Offline
#3 2006-05-28 14:27:26
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: How do you find X?
So the xth root of n is x, I see.
Hey are logs totally different from roots, I guess they are, because roots talk about the exponent, but logs talk about the base, the thing to be powered.
What about log base x of n is x?
Ganesh's puzzle said that log 8/log 2 is 3 because 2^3 is 8.
Hmm, I'm stuck. log n/log x is x because x^x is n. Oh, well that is something I guess.
igloo myrtilles fourmis
Offline
#4 2006-05-28 14:33:30
- RickyOswaldIOW
- Member

- Registered: 2005-11-18
- Posts: 212
Re: How do you find X?
I know nothing about log ![]()
2² = 4 and ²√4 = 2
5³ = 125 and ³√125 = 5
so
So the xth root of n is x, I see.
x^x = n and x√n = x ![]()
Aloha Nui means Goodbye.
Offline
#5 2006-05-28 15:10:12
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: How do you find X?
If the number n is converted to a different base, then if the number has approximately x digits left of the decimal place and the base is also x, then you may be close.
For example 10^10 is a 1 with ten zeros after it in base 10.
And 2^2 is a 1 with 2 zeros after it in base 2.
And 3^3 is a 1 with 3 zeros after it in base 3.
And 4^4 is a 1 with 4 zeros after it in base 4.
I think its funny! LTS (laugh to self)
igloo myrtilles fourmis
Offline
#6 2006-05-28 17:01:41
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: How do you find X?
lothy, they only way I know how to solve a problem like this is to do an approximation method. Find a value for which x^x > n, and find a value where x^x < n. Then take the average of that value, and see if it is greater or less than n. Use this as your new value, and repeat. It might make more sense if I write it out in pseudocode:
Find a, where a^a > n
Find b, where b^b < n
Start loop here:
Let c = (a + b) / 2 //the average of a and b
If c > n
Let b = c
If c < n
Let a = c
Go back to the top of the loop, repeating until you get the accuracy you want.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#7 2006-05-28 17:09:28
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: How do you find X?
Is there only one solution to the problem x^x = n? Its kind of hard to visualize.
x√n = x
I'm not sure what the point of that is, just looks like a rearranged form of the same question.
A logarithm is just a misspelled algorithm.
Offline
#8 2006-05-28 17:33:51
- luca-deltodesco
- Member

- Registered: 2006-05-05
- Posts: 1,470
Re: How do you find X?
so using logarithms, we also get rearranged
and ofcouse neither this or the root one is a formula for x, since it cant be calculated with just being given n
Last edited by luca-deltodesco (2006-05-28 17:39:17)
The Beginning Of All Things To End.
The End Of All Things To Come.
Offline
#9 2006-05-28 18:56:25
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: How do you find X?
Here is the code for approximating solutions:
#include <iostream>
#include <math.h>
using namespace std;
int min(double n)
{
for (int x = 0; x <= n; x++)
{
if (pow(x, x) > n)
{
return x-1;
}
}
}
int max(double n)
{
for (int x = n; x > 0; x--)
{
if (pow(x, x) < n)
{
return x+1;
}
}
}
int main()
{
for (int n = 2; n < 30; n++)
{
double a = min(n);
double b = max(n);
double c;
for (int x = 0; x < 100; x++)
{
c = (a + b) / 2.0;
if (pow(c, c) > n)
{
b = c;
}
else
{
a = c;
}
}
cout << n << ". " << c << endl;
}
return 0;
}That will generate numbers 2 through 29. You can also use this for decimal values as well. Just make n whatever you want.
As for the results:
2. 1.55961
3. 1.82546
4. 2
5. 2.12937
6. 2.23183
7. 2.31645
8. 2.38842
9. 2.45095
10. 2.50618
11. 2.5556
12. 2.6003
13. 2.64106
14. 2.67852
15. 2.71316
16. 2.74537
17. 2.77545
18. 2.80366
19. 2.83022
20. 2.85531
21. 2.87907
22. 2.90164
23. 2.92312
24. 2.94362
25. 2.96322
26. 2.98199
27. 3
28. 3.01731
29. 3.03396
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#10 2006-05-29 01:51:27
- RickyOswaldIOW
- Member

- Registered: 2005-11-18
- Posts: 212
Re: How do you find X?
number n is converted to a different base
I think I see what you mean by this:
2^2 is a 1 with 2 zeros after it in base 2 so x^x is a 1 with x zeros after it? But lothy did specify
(x power of x)
To solve it exactly, I would agree that it's impossible since we have no values given to work with so we can only approximate. I did not know we could do this previously but what you guys are saying seems to make sense ![]()
Aloha Nui means Goodbye.
Offline
#11 2006-05-29 02:00:15
- RickyOswaldIOW
- Member

- Registered: 2005-11-18
- Posts: 212
Re: How do you find X?
Are you studying high/advance level maths lothy or are you a school student?
Aloha Nui means Goodbye.
Offline
#12 2006-05-29 17:48:15
- Zmurf
- Member
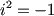
- Registered: 2005-07-31
- Posts: 49
Re: How do you find X?
You can also express it as something like the following.
250 = x^x
x^x = 4^4 - 2^2 - 1^1 - 1^1.
Is there anway to take the collection of these numbers arrange them to accurately form x^x?
Heres my C++ app for finding an appraximation for x:
// System Includes.
#include <iostream>
#include <math.h>
// Other Includes.
// Namespaces.
using namespace std;
// Main Function.
int main(){
// Variables.
double n = 0.0;
double x = 0.0;
double step = 1.0;
double out = 0.0;
// Interface.
cout << "n = x^x" << endl;
cout << "n = ";
cin >> n;
// Calculations.
for (x = 1.0; x < 16.0; x += step){
if (pow(x, x) == n){
cout << "x = " << x << endl;
break;
}
else if (pow(x, x) > n){
if (step < 0.0001){
cout << "x = " << x << endl;
break;
}
x--;
step /= 10;
}
}
// Let user see display.
system("PAUSE");
// Return no value.
return 0;
}Last edited by Zmurf (2006-05-29 18:02:44)
"When subtracted from 180, the sum of the square-root of the two equal angles of an isocoles triangle squared will give the square-root of the remaining angle squared."
Offline
#13 2006-06-02 01:18:53
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
Interesting theme.
I'll post something after a while...
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#14 2006-06-02 02:00:41
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
A plot of x^x:
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#15 2006-06-02 02:13:07
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
Can't we got some series for f^-1(x)?
Using series:
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#16 2006-06-02 02:23:11
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
Only a note- the minimum of the function is at
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#17 2006-06-02 03:16:36
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
The answer is the function:
where W is the productlog function.
So you can compute it directly.
edit: sorry but the first function was incorrect.
Last edited by krassi_holmz (2006-06-02 04:26:54)
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#18 2006-06-02 03:19:46
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: How do you find X?
What is y? And can you write out W?
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#19 2006-06-02 04:29:45
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
What is y? And can you write out W?
Sorry. I assumed that:
and so we're searching x by using y.
For the product log, wikipedia helps much. There's something I'm using to make my own program.
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#20 2006-06-02 04:37:32
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
Here's my program-based on requrent computation of the power log omega.
#include<iostream>
#include<math.h>
using namespace std;
int const pr=10;
double const e=2.7182818284590452354;
double const l2=0.69314718055994530942;
double omega(int n,double x);
int main(){
st: cout<<"Input y (y>1)(0 for quit):";
double y;
cin>>y;
if(y==0.) goto en;
cout<<"The solution of x^x="<<y<<" is:"<<pow(e,omega(pr,log(y)))<<".\n";
goto st;
en: cout<<"Press any key to continue..."<<endl;
char c;
cin>>c;
return 0;
}
double omega(int n,double x){
if(n==0){
return 0;
}
else{
double om=omega(n-1,x);
double omp=pow(e,om);
double result=om-(om*omp-x)/(omp*(om+1)-((om+2)*(om*omp-x))/(2*om+2));
return result;
}
}I'm making tests now. The presiesility may be changed by changing pr.
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#21 2006-06-02 04:42:02
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
Here's a copy of the command prompt:
Input y (y>1)(0 for quit):12089258196146291747061760000000000000000000000000000000000000000
The solution of x^x=1.20893e+064 is:40.
Input y (y>1)(0 for quit):24806364445134114549464918239541268974453058149265416432172060012817382
8125
The solution of x^x=2.48064e+074 is:45.
Input y (y>1)(0 for quit):24889437491384718234
The solution of x^x=2.48894e+019 is:16.0794.
Input y (y>1)(0 for quit):123408471204832479128412342406123046213749812462891384761234
The solution of x^x=1.23408e+059 is:37.5324.
Input y (y>1)(0 for quit):13240127341289348712634981271478293647123058734122348329472198034861239
4712349
The solution of x^x=1.32401e+077 is:46.3026.
Input y (y>1)(0 for quit):IPBLE: Increasing Performance By Lowering Expectations.
Offline
#22 2006-06-02 04:43:35
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
It crashed for y=50^50. I'll see what's the maximum.
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#23 2006-06-02 04:45:47
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
The limit is: 47^47=3877924263464448622666648186154330754898344901344205917642325627886496385062863
What would you say? ![]()
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#24 2006-06-02 04:53:59
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
No, that's not the limit. It solved 87^87!!!
IPBLE: Increasing Performance By Lowering Expectations.
Offline
#25 2006-06-02 04:55:59
- krassi_holmz
- Real Member

- Registered: 2005-12-02
- Posts: 1,905
Re: How do you find X?
It works for all doubles.
IPBLE: Increasing Performance By Lowering Expectations.
Offline