Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2006-04-29 13:26:06
- renjer
- Member
- Registered: 2006-04-29
- Posts: 50
Line Integral of a Helix from Point A to B
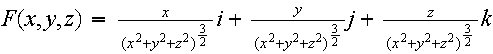
is a vector field. Now how do I evaluate the line integral F.dr in the region C where C starts at the point A(12,0,0), ends at point B (0,12,5) and is an arc on the helix:
x=12cos πt
y=12sin πt
z=2t
where π is the number pi.
I know how to evaluate line integrals for a helix and using F but now with the points added in (point A and B) I have no idea how to begin. Please help.
Offline
#2 2006-04-29 13:54:22
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: Line Integral of a Helix from Point A to B
First, find the limits of integration. That is, find the start and endpoints of your path.
A = (12,0,0) B = (0,12,5)
x=12cos(pi*t)
y=12sin(pi*t)
z=2t
So we want (12cos(pi*t), 12sin(pi*t), 2t) = (12, 0, 0). So it must be that 2t = 0. Thus, t = 0. Try the other ones, and you'll see that they work as well.
Now we want (12cos(pi*t), 12sin(pi*t), 2t) = (0, 12, 5). Again, 2t = 5, so t = 5/2. You can check the others, but it will work out.
So we know that 0 <= t <= 5/2. These are the limits of integration.
Remember that:
So we need to find F(c(t)) and c'(t). Once you find these, take the dot product, and then integrate.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
Pages: 1