Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2006-03-16 09:16:21
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Water pressure
Me and my dad were argueing about water pressure one night, poking holes in a milk bottle and filling it with water for experiments. I noticed something interesting. We had holes poked at several different heights. When the bottle was full, the streams for water seemed to connect at almost the same point. However, when the water level got close enough to a hole, the stream slows to a trickle and eventually stops when the water sinks below it. From this I theorize perhaps, in a container filled with water to a vast height, if the holes are horizontally alligned, the streams will tend to intersect in the same place.
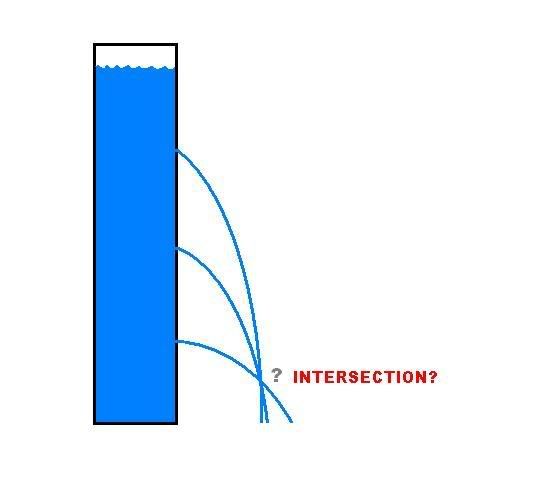
This is just a guess I want to try to figure out if its true. But there are a few things I need to figure out. First I need to say, I don't necessarily think they intersect as the water height tends to infinity. With an infinite water height, the streams coming out would be horizontal and may never intersect! Therefore I think its better just to use managable large theoretical values like 100 or 1000 feet or meters. In calculus, I learned how to find the pressure excerted by water at a given depth, but what I don't know is, how do I translate pressure into velocity when the water comes shooting out?
A logarithm is just a misspelled algorithm.
Offline
#2 2006-03-16 10:03:52
- ryos
- Member

- Registered: 2005-08-04
- Posts: 394
Re: Water pressure
You do a mechanical energy conversion. Since water is incompressible, when it exits the hole its pressure immediately drops to 1 atmosphere and all of the potential energy it had in the form of pressure is converted to kinetic.
I'm at work so I don't have my books, but when I get home I can give you the equations.
El que pega primero pega dos veces.
Offline
#3 2006-03-16 10:25:05
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Water pressure
Thanks!
A logarithm is just a misspelled algorithm.
Offline
#4 2006-03-16 14:50:48
- George,Y
- Member

- Registered: 2006-03-12
- Posts: 1,379
Re: Water pressure
Once I read this problem in a calculus book. the key is a water particle escaping from the hole has a initial velocity ( Sqrt(2gh), 0 ), where h is the depth. The water particle used to be balanced by all other particles around it and the bottle, thus no wonder the velocity is horizontal. But how the magnitude is determined seems to be a physics theorem.
X'(y-Xβ)=0
Offline
#5 2006-03-16 17:00:38
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,711
Re: Water pressure
This will no doubt start off ryos's new subject of "Probaballistics"
BTW I saw this in action one day. A guy on a building site drilled a small hole in a circular column. The column was several meters high, made of steel and hollow inside. And (strangely) full of water!
The water shot out almost horizontal through the tiny hole and ended up hitting the ground some meters away. It kept coming out of the hole for a long time, with the landing point gradually getting closer and closer to the column. Fun to watch.
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#6 2006-03-16 17:14:39
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Water pressure
perhaps thats why he drilled the hole?
What were you doing on a building site?
A logarithm is just a misspelled algorithm.
Offline
#7 2006-03-16 19:03:10
- ryos
- Member

- Registered: 2005-08-04
- Posts: 394
Re: Water pressure
George,Y's equation is derived from potential energy. Gravitational potential energy is U = mgh. Kinetic energy is K = 1/2 mv². Given that energy is conserved, U = K, so mgh = 1/2 mv². Solving for v gives sqrt (2gh).
This solution assumes that the potential energy due to pressure is the same as gravitational potential energy. It makes a kind of sense, because the fluid pressure in an open-air container arises due to gravity.
This problem can be about as complex as you want it to be. For example, as the water flows out of the tank, the fluid level falls, as does the pressure, so you have to take those rates into account. You can determine the flow rate based on the diameter of the hole and the pressure, but the flow rate also varies with depth.
The arc of the water is influenced by air resistance in a complex way.
Etc., etc., etc. You get the idea.
BTW, one useful little formula is P/ρ, or pressure/density, which gives the energy of a fluid under pressure per unit mass (J/kg).
Sorry if this is incoherent, my brain is fried from the physics test I just took.
El que pega primero pega dos veces.
Offline
#8 2006-03-16 19:07:23
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: Water pressure
Mikau, did you make all the holes about the same size for your test?
Sounds interesting.
What was the diameter of the holes, out of interest?
igloo myrtilles fourmis
Offline
#9 2006-03-17 06:30:43
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Water pressure
we tried to make the holes all the same size, about 1/8 inch, but later we found a larger hole seemed to squirt as far as a small one, just with more water.
Yeah Ryos this problem is as complex as we make it. But I'm not trying to land a rocket. What I'm most interested is, will the weight and the water and the height of the fall ballance out such that all the streams intersect in the same place.
sqrt (2gh) ? What does g stand for here?
A logarithm is just a misspelled algorithm.
Offline
#10 2006-03-17 07:10:12
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: Water pressure
g = Gravitational field strength.
Assuming you don't live on a really tall mountain or on the moon or anything, this can be taken as:
9.81 ms[sup]-2[/sup]
Edit because it looked weird before.
Last edited by mathsyperson (2006-03-17 07:12:25)
Why did the vector cross the road?
It wanted to be normal.
Offline
#11 2006-03-17 07:38:54
- ryos
- Member

- Registered: 2005-08-04
- Posts: 394
Re: Water pressure
g is the acceleration due to gravity, or 9.8 m/s². Note also that h is depth, not height (measured from the top of the water, not the bottom).
The position equation for a particle in free fall (where the position is r) is:
Note that r, v and g in this equation are vector quantities. For our case this is fairly simple to deal with because the initial velocity has only an x component and g has only a y component. So, the v term contributes to the x component of r, and the g term contributes to the y.
So, the x position at a given time t is given by:
And the y position at t is:
You should be able to use these to find the intersection. Have fun. ![]()
El que pega primero pega dos veces.
Offline
#12 2006-03-17 10:24:26
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Water pressure
so velocity of x = Sqrt(2(-9.8h) ? I know how to work the vertical position but the horrizontal velocity equation still seems unclear.
A logarithm is just a misspelled algorithm.
Offline
#13 2006-03-17 15:10:29
- George,Y
- Member

- Registered: 2006-03-12
- Posts: 1,379
Re: Water pressure
Both velocity and acceleration are vectors. All vectors can be decomponented into a sum of inter-perpendicular vectors. perpendicular means they don't interfere each other. in this case, a vector can be decomponented to a horizontal one and a verticle one, (eg Sqrt(2gh) i and 0j, where i and j stand for horizantal and verticle unit vector) and the verticle component of the acceleration does not influence the horizontal componet , like g doesn't interfere horizontal velocity.
Thus a motion containing accelerations and velocities and displacements can be decomponented into 3 dimensions.
here 2-d is enough.
horizontally, no a, so v constantly √(2gh) thus displacement sx=v t, where sx stands for horizontal displacement.
vertically, a=g, v0=0 so vt = at = gt, displacement sy=1/2(v0+vt)t = 1/2 a t^2 = 1/2 g t^2
now we know after a certain time t, sy=d,
solve t out, t=√(2d/g)
sx=v t = √(2gh) √(2d/g)= 2√(hd)
sx=2√(hd), when sy=d
t is not contained in this formula, and it applies to water particle escaping from any holes. it states its horizontal displacement after having fallen distance d.
uh o, it seems a lot of difficulty to go further, lazy person like i would like to pass it onto next solver...![]()
Last edited by George,Y (2006-03-17 15:14:49)
X'(y-Xβ)=0
Offline
#14 2006-03-18 06:25:07
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Water pressure
hmm I guess I'm not too familiar with vector terminalogy. Now I'm just confused. I have worked with them in calc but mostly simple stuff I think. I want to take vector calculus (and every other form of calculus)
Simply put: the position of x should be a function of t. x = p(t) what is p(t)? Or V(t) for velocity, and I can integrate to get position. Perhaps I need to get my hands on a physics book. :-/
A logarithm is just a misspelled algorithm.
Offline
#15 2006-03-18 10:08:24
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,711
Re: Water pressure
I would look at it as simple projectile motion.
* The water jets out with a certain horizontal velocity, which you could assume stays constant (ignoring air friction).
* The vertical velocity starts at 0, and increases by 9.81 m/s every second (ie g=9.81 m/s²) due to gravity.
BUT figuring out the horizontal velocity is the trick, and it depends mostly on the pressure of water (which increases with depth), but partly on the hole (friction mainly). George,Y's reference said the horizontal velocity would be Sqrt(2gh), but this may only be an approximation.
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#16 2006-03-18 10:20:37
- ryos
- Member

- Registered: 2005-08-04
- Posts: 394
Re: Water pressure
Vectors aren't that hard to understand--they're just a major pain to work with.
A vector is a quantity having both magnitude (meaning length) and direction. Think of a vector as an arrow drawn in coordinate space. Vectors don't have position, so you can place them anywhere you like in coordinate space, and as long as you don't altar their direction or magnitude, all is well.
Unit vectors are a convenient way to separate a vector into its component parts. A unit vector has magnitude 1 and is directed along one of the coordinate axes. The unit vector for x is called i, y is called j, and z is called k. They're written with a little hat (^) on top, like this: î (don't know if that'll come through).
So, a vector that has magnitude 5 and is directed 30 degrees above the horizontal has components (4)i and (3)j. If you add them together (using vector addition), they produce the final vector.
You can read more about them on your own. But, you don't need to know much about vectors to solve this problem. You can use the one equation to find the x position, and the other to find the y, and see if, at any one time, the three are the same. Like George, I'm too lazy to work it out for you, but it may involve systems of equations, graphing, and the like.
El que pega primero pega dos veces.
Offline
#17 2006-03-18 11:33:03
- Ricky
- Moderator

- Registered: 2005-12-04
- Posts: 3,791
Re: Water pressure
Vectors don't have position, so you can place them anywhere you like in coordinate space, and as long as you don't altar their direction or magnitude, all is well.
That is completely true, in lower mathimatics. But when you get to upper level calculus, you start dealing with things such as vector fields, and there, vectors most certainly have a position.
"In the real world, this would be a problem. But in mathematics, we can just define a place where this problem doesn't exist. So we'll go ahead and do that now..."
Offline
#18 2006-03-19 15:19:29
- George,Y
- Member

- Registered: 2006-03-12
- Posts: 1,379
Re: Water pressure
midhole spays furtherst, if the bottle is placed on ground.
the position of x should be a function of t. x = p(t)
- can we use a cartesian co-ords? A water particle's position is
(x,y)= (x(t),y(t)) , in which x is the horizontal distance from bottle, y is the height it has fallen
define d= depth
x= √(2dg) t (1)
y= g t^2 /2 (2)
solving 2 for t gets
t= √(2y/g)
hence x can be expressed an explicit function of y as
x=2 √(dy)
if you place a full bottle on the ground, a hole at 1/n height of bottle and another hole at 1-1/n height will have their water stream intersect on the ground.
but the hole at the mid point will spray water further, with x=2d , the same as bottle height, when y= d = 1/2 bottle height
X'(y-Xβ)=0
Offline
#19 2006-03-19 20:19:27
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,711
Re: Water pressure
By the way George, it is great to have you on the forum!
Would you like to formally "Introduce" yourself in the Introductions section, so we can all know more about you, where you live, your passions, etc. ![]()
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#20 2006-03-20 00:28:18
- George,Y
- Member

- Registered: 2006-03-12
- Posts: 1,379
Re: Water pressure
Thank you, i will do it
X'(y-Xβ)=0
Offline
#21 2006-03-23 02:43:58
- George,Y
- Member

- Registered: 2006-03-12
- Posts: 1,379
Re: Water pressure
My recent experiment showed the difference between a theory and reality ![]()
X'(y-Xβ)=0
Offline
Pages: 1