Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2006-01-20 06:39:53
- Graeme
- Member
- Registered: 2006-01-19
- Posts: 15
Circle And Square
Here's a new one for you maths brains to puzzle over ![]() Though I'm sure it's not TOO difficult.
Though I'm sure it's not TOO difficult.
In the diagram linked, the square has two of its vertices on the circle and the other two lie on a tangent to the circle. What is the ratio of the area of the square to the area of the circle?
Offline
#2 2006-01-20 08:09:02
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: Circle And Square
I have to attribute this solution to my dad. I showed him this problem and he recalled a method I used to solve another problem which I had showed him and how it could be applied here. (Remember the circle with the four 20 degree inscirbed angles? Thats the one)
Anyways, all we're concerned about is the ratio, so we can assign values to either the circle or the square (but not both) and find the area of the other in terms of the first.
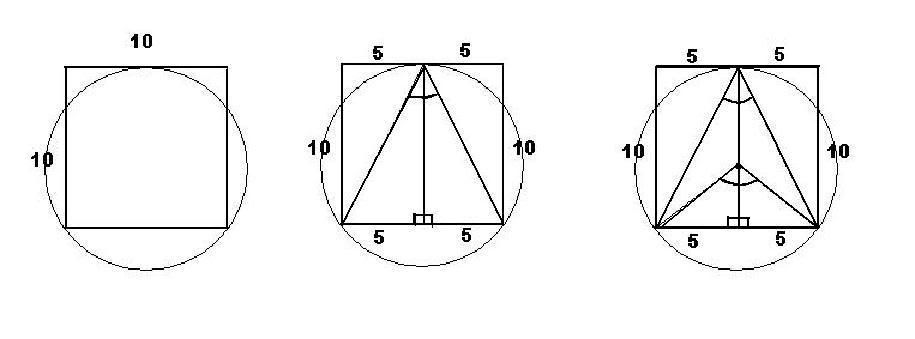
Lets start by letting the square be 10 by 10. If we divide it in two and draw diagonals, we have drawn an inscribed angle inside the circle. The length of this incribled angle is 2 arctan(5/10) thus the measure of the intersecpted arc will be 4 arctan(5/10). We can now draw an angle from the center of the circle to the edges of this arc to find the middle angle. Divide it by 2 to find the angle of a right triangle with a leg of 5. We can now find the radius using trig and solve the problem. :-)
Last edited by mikau (2006-01-20 08:16:06)
A logarithm is just a misspelled algorithm.
Offline
Pages: 1