Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2006-01-18 01:25:58
- Graeme
- Guest
A sphere problem
Three spherical balls, each of radius 15cm are placed in a hemispherical bowl in such a way that they touch each other and each one touches the inside of the bowl. The tops of the balls are all perfectly level with the top of the bowl. What is the bowl's radius?
Thanks for any help
#2 2006-01-18 09:47:47
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
This one was pretty tough being that it really needs to be done in three dimensions.
If you were to look at this hemisphere from the side in line with the point where two of the spheres are touching you would notice that one of the spheres is contained within a 90° arc of the hemisphere. The center of the hemispherical arc coincides with the outer edge of the smaller sphere and the top of the smaller sphere is aligned with the top of the hemisphere. You will notice that a bisector through the center of the sphere from the center of the top of the bowl? will give you the hypotenuse of a triangle whose sides are two dimensions of the three needed. Sorry, I can't draw.
In three dimensions;
R(bowl) = √(x²+y²+z²)
Call the two dimensions above x and z, because x would be the diffence from the center and z would be the difference from the top. Call the hypotenuse B and the radius of the circle r and the space between the circle and the corner s.
The bisector line is 45° below the rim of the bowl so B = r + (r + s)
Because (r+s) is the hypotenuse of the little triangle with sides r, (r+s) = √(2r²)
Now B = r + √(2r²)
Because B = √(x² + z²), B² = x² + z²
B² = r²(3 + √8)
Now for y.
If you now look at the bowl from overhead you will see point B with an offset y from the center of the bowl. This is where it gets tricky.
The centers of the three cirles form an equilateral triangle sharing a geometrical center with the bowl. The distance from this center to the center of the circle containing point B is given by;
sin120°/(2r) = sin30°/y
So y = 2rsin30°/sin120
Now back to the main question, what is R? From what we have seen;
R = √(B² + y²)
Plugging in all of the given numbers gives;
R ≈ 40.142..
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#3 2006-01-18 09:52:00
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
By the way. Graeme, where do you come up with the incredible questions? I still haven't figured out the last one you asked. I am thinking that you are not who you pretend to be.
Should I have solved this as a "Guest"?
Last edited by irspow (2006-01-18 09:53:52)
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#4 2006-01-18 10:07:07
- mathsyperson
- Moderator

- Registered: 2005-06-22
- Posts: 4,900
Re: A sphere problem
There haven't been any posts from that IP address apart from his, so that suggests that Graeme is who he says he is.
Why did the vector cross the road?
It wanted to be normal.
Offline
#5 2006-01-18 12:36:22
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: A sphere problem
It is an interesting problem. I think I could solve it but not in a formal way. (naming the postulates and axioms, etc.)
I really need to review geometry. Did algebra 2 so fast it was like a fleeting dream...
A logarithm is just a misspelled algorithm.
Offline
#6 2006-01-18 16:01:06
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
Didn't I solve it already? Just kidding mikau. I would love to see another solution. I struggled with that one a little, so I would tend to think that there may be a simpler method.
Mathsyperson, couldn't Graeme have two computers?
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#7 2006-01-19 02:24:09
- Graeme
- Guest
Re: A sphere problem
Hi,
I am actually a guest, no one else. I should really become a member though ![]()
I have a different solution to the problem, so can you see any errors in mine?
Solution:
We take the radius of the dish through the centre of one of the balls. Therefore the radius will be 15(ie. radius of ball) + (distance from centre of ball to centre of bowl)
The latter distance is the hypotenuse of a right angled triange (oriented in the vertical plane through the centres of bowl and ball) with a horizontal leg from the centre of the dish to the top of the ball (i.e where they are level). The vertical leg is from the top of the ball to the centre of the ball (ie, the radius).
Using Pythagoras' Theorem we can find the distance from the centre of the ball to the centre of the dish by creating an equilateral triangle through the centres of the three balls, with the triangles sides being 30cm (2 ball radii). This results in the distance from the centre of one ball to the centre of the dish being 30/(sqrt)3
If we put this into the vertical triange then we have two sides of length 15cm and and 20/(sqrt)3 respectively. We can then use Pythagoras' Theorem to finish the problem as:
AB^2= AC^2 + CB^2
= (30/(sqrt)3)^2 + (15)^2
= 900/3 + 225
= 1575/3
AB = sqrt (1575/3)
= 22.912.. +
Therefore the radius of the bowl equals:
15 + 22.912.. +
= 37.912 to 3 d.p
Does there seem to be any error in this solution?
Thanks
Graeme
#8 2006-01-19 09:45:59
- MathsIsFun
- Administrator

- Registered: 2005-01-21
- Posts: 7,713
Re: A sphere problem
Good question!
Yes, you can become a Member, and then tell us a bit about yourself in Introductions. ![]()
"The physicists defer only to mathematicians, and the mathematicians defer only to God ..." - Leon M. Lederman
Offline
#9 2006-01-19 10:23:14
- Graeme
- Member
- Registered: 2006-01-19
- Posts: 15
Re: A sphere problem
I finally became a member lol. Now irspow can find out who I am ![]()
Anyway, thanks for any help with my solution i posted
Offline
#10 2006-01-19 11:07:35
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
Graeme, welcome to the forum. I didn't mean anything by my obviously incorrect assumptions aout you. I just thought that the level of difficulty in the problems that you have posted smelled more of a moderator playing around with the mere mortals around here.
I ran my calculations over two more times to be sure that they were correct. I can not pinpoint where your error lies, however I can tell you that I got the same distance for the space from the center of one ball to the center of the bowl. The only problem was that I computed this distance horizontally along the surface and not as an extention of an angle hypotenuse. I would think that the way that you are using it, it should be larger.
My problem is that I am having a hard time visualizing what orientation that you are using. I have absolutely no idea how you are constructing a single triangle with a vertice at the center of the bowl, and a vertice at the center of a circle to find the radius.
Are you sure that you have not solved this in some way considering only two dimensions? I myself did exactly that twice before getting on the correct track.
I will see if I can post pictures of how I solved it later. If you could do the same then I am sure I can find your error.
Again, welcome to the forum, and have a good time.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#11 2006-01-19 12:10:14
- Graeme
- Member
- Registered: 2006-01-19
- Posts: 15
Re: A sphere problem
Thank you very much irspow for your kind words and help with this.
I will post pictures of my possible solution as soon as possible (within 24 hours hopefully) and hopefully it can clear things up about my idea.
Thanks again
Offline
#12 2006-01-19 14:05:54
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: A sphere problem
This one was pretty tough being that it really needs to be done in three dimensions.
Thats what I thought irspower, but with a little care and a nifty observation, it can be solved in 2d.
Take a look at my pic. Its pretty much self explanatory.
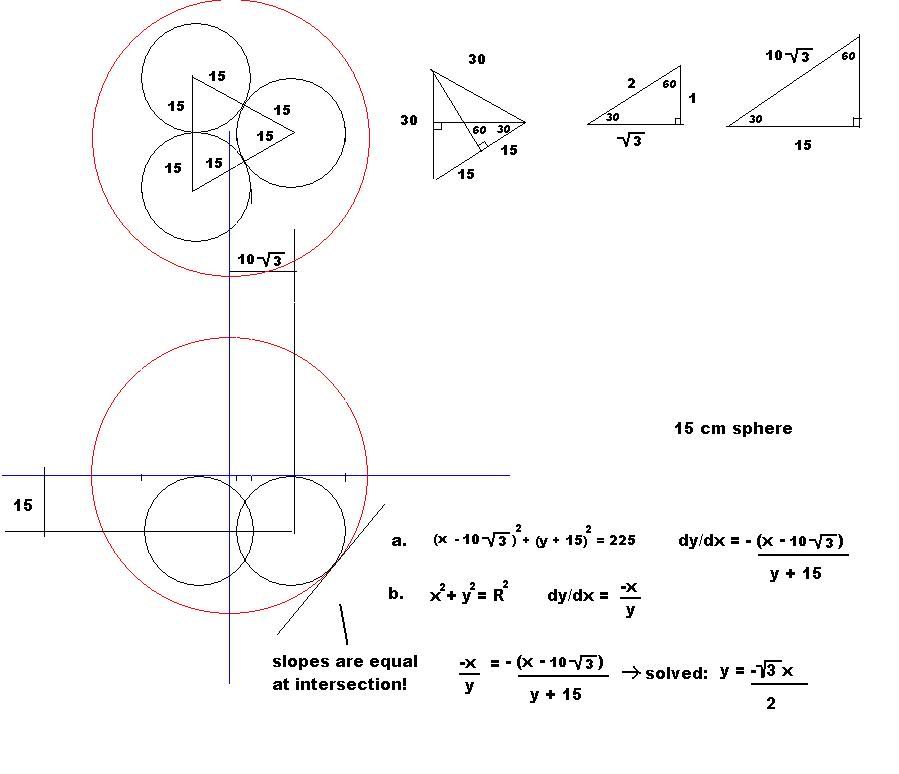
The key to this problem is the slopes of the two cirlces are equal at the intersection. This gives us an extra equation that does not contain R. Then we have two equations for x and y that do not contain R. We can then solved for y in terms of x. Substitute this value of x in equation a to solve for x, then solve for y. Once we have the values of x and y we can use equation b to find the radius.
In the end I got the same answer Greame did, so I guess thats the correct answer.
The slope observation I think is an interesting one that I never made before. Its very usefull in finding the intersection of tangent circles and the size of tangent circles (as in this case). A circle of an unkown radius, with a given centerpoint, can intersect a given circle, at an infinite number of points. But there are only two points for which they intersect, and are tangent, the points of intersection where the slopes are equal. That gives us an extra equation to find the intersection. :-)
Last edited by mikau (2006-01-19 14:10:14)
A logarithm is just a misspelled algorithm.
Offline
#13 2006-01-19 14:50:18
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: A sphere problem
Just read greame's solution and its much simpler. Pretty much the same as mine only uses geometry rather then equations. Works just as well only its faster, so I'd say his is the best way to do it. Still I'm proud of my equal slopes observation. :-)
A logarithm is just a misspelled algorithm.
Offline
#14 2006-01-19 14:55:51
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: A sphere problem
Come to think of it, my not noticing I could use graeme's method was so idiotic its unreal. My equation and graph skill is much higher then my geometry. In my oppinion the simplest solution is the best and graeme's was the simplest. Hats off to you graeme!
Great problem!
A logarithm is just a misspelled algorithm.
Offline
#15 2006-01-19 15:08:02
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
Once again, I show my stupidity....I couldn't figure out how to do it in two dimensions, much less using a single sphere, all the while making it much more difficult.
Thanks for the proof and the visualization. Now I can see exactly how Graeme was looking at the problem.
Graeme, sorry for any inconvenience that I may have caused you.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#16 2006-01-19 15:12:08
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: A sphere problem
heres a drawing of how graeme did it. I take it he found the center coordinates of the small circle same as I did. Then just used the pythagorean theorem plus the radius.

A logarithm is just a misspelled algorithm.
Offline
#17 2006-01-19 15:13:18
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: A sphere problem
I wonder if this problem would be more difficult if the bowl size was given, but not the ball size.
A logarithm is just a misspelled algorithm.
Offline
#18 2006-01-19 15:26:28
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
r(ball) = R(bowl) / [1 + √(7/3)]
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#19 2006-01-19 16:03:30
- mikau
- Member

- Registered: 2005-08-22
- Posts: 1,504
Re: A sphere problem
Maybe. I'm not sure where you got that formula.
I think the reason I didn't see the obvious solution was I did not assume the line drawn from the small circle to the edge of the large, had the angle as the line from the center of the large circle to the point of tangency.
Lets see if I can prove it.
(edit) dang. It seems obvious enough but I can't seem to prove it. I'll keep working on it but maybe you guys can get it before me.
Prove this!
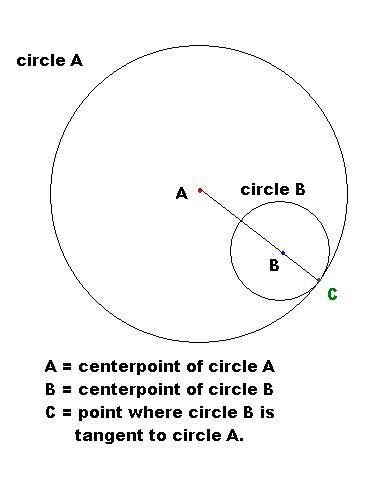
If a small circle B is inside a large circle A, and circle B is tangent to circle A at point C, prove the line drawn through point A to point B passes through the point C. (the point of tangency). Point A and point B are the centerpoints of circles A and B.
Last edited by mikau (2006-01-19 16:50:51)
A logarithm is just a misspelled algorithm.
Offline
#20 2006-01-19 16:31:22
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
I just worked the now easy problem in reverse.
if R = radius of bowl and r = radius of ball and C = number of balls
C = 1; R = 2r
C = 2; R = r(1 + √2) ≈ 2.414r
C = 3; R = r(1 + √(7/3)) ≈ 2.527r
C = 4; R = r(1 + √3) :asmp 2.732r
C = 5; R = r(1 + √[(4sin²54°)/(sin²72°) + 1]) ≈ 2.973r
C = 6; R = r(1 + √5) ≈ 3.236r
C = 7; R ≈ 3.512r
C = 8; R ≈ 3.798r
In general for this equation;
R = r(1 + √((4sin²a / sin²b) + 1))
where a = [180 - (360/C)] / 2 and b = 360/C and C = number of balls.
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
#21 2006-01-20 04:14:07
- Graeme
- Member
- Registered: 2006-01-19
- Posts: 15
Re: A sphere problem
Maybe. I'm not sure where you got that formula.
I think the reason I didn't see the obvious solution was I did not assume the line drawn from the small circle to the edge of the large, had the angle as the line from the center of the large circle to the point of tangency.
Lets see if I can prove it.
(edit) dang. It seems obvious enough but I can't seem to prove it. I'll keep working on it but maybe you guys can get it before me.
Prove this!
http://i21.photobucket.com/albums/b299/ … raeme2.jpg
If a small circle B is inside a large circle A, and circle B is tangent to circle A at point C, prove the line drawn through point A to point B passes through the point C. (the point of tangency). Point A and point B are the centerpoints of circles A and B.
I have an explanation/proof for the line and the points for spheres, however I presume it works in principle for circles also.
Whenever two spheres touch each other (one inside the other or outsides touching), their point of contact will be on the line through their centers. You can see this intuitively if you simplify the problem and picture one ball at the bottom of the bowl--clearly the contact is at the very bottom of the bowl. (You can prove this rigorously by rotating the bowl and sphere about the line connecting their centers. The bowl and
sphere will remain in place because of their symmetry, so their point of contact must as well, meaning it is on the line of symmetry, which only touches the bowl at the bottom). Back to this more complex case, if you froze the spheres in place in the bowl and rolled the bowl so that you look straight down through its center and through the center of one of the balls, it looks exactly like the one-ball case (with two extra balls in the way).
Offline
#22 2006-01-20 04:25:23
- Graeme
- Member
- Registered: 2006-01-19
- Posts: 15
Re: A sphere problem
Come to think of it, my not noticing I could use graeme's method was so idiotic its unreal. My equation and graph skill is much higher then my geometry. In my oppinion the simplest solution is the best and graeme's was the simplest. Hats off to you graeme!
Great problem!
Thank you very much mikau.
Offline
#23 2006-01-20 04:27:01
- Graeme
- Member
- Registered: 2006-01-19
- Posts: 15
Re: A sphere problem
Once again, I show my stupidity....I couldn't figure out how to do it in two dimensions, much less using a single sphere, all the while making it much more difficult.
Thanks for the proof and the visualization. Now I can see exactly how Graeme was looking at the problem.
Graeme, sorry for any inconvenience that I may have caused you.
No problem at all, I appreciate all sorts of approaches to problems. Since I am only young, I haven't even touched on the more complex maths, so alternative approaches are always interesting.
Offline
#24 2006-01-20 04:40:22
- Graeme
- Member
- Registered: 2006-01-19
- Posts: 15
Re: A sphere problem
I just worked the now easy problem in reverse.
if R = radius of bowl and r = radius of ball and C = number of balls
C = 1; R = 2r
C = 2; R = r(1 + √2) ≈ 2.414r
C = 3; R = r(1 + √(7/3)) ≈ 2.527r
C = 4; R = r(1 + √3) :asmp 2.732r
C = 5; R = r(1 + √[(4sin²54°)/(sin²72°) + 1]) ≈ 2.973r
C = 6; R = r(1 + √5) ≈ 3.236r
C = 7; R ≈ 3.512r
C = 8; R ≈ 3.798r
In general for this equation;
R = r(1 + √((4sin²a / sin²b) + 1))
where a = [180 - (360/C)] / 2 and b = 360/C and C = number of balls.
Could you please explain how you worked out this formula. Apologies for the trouble but I can't really work it out.
Maybe it's too early and i'm tired ![]()
![]()
Offline
#25 2006-01-20 09:15:55
- irspow
- Member

- Registered: 2005-11-24
- Posts: 1,055
Re: A sphere problem
Graeme, I am sure that you can look back at all of those wonderful illustrations from earlier in this topic to imagine the lines to which I am referring. Remember how we determined the distance from the center of the bowl to the center of one of the balls? We solved for the distance between balls and the center by creating a geometric figure with each ball's center as a vertice.
In the example above there were only three, forming a triangle, but any number of balls will form some sort of polygon. And any of those polygons will have a geometric center that is equidistant from all of the balls centers.
If you look at any side of one such polygon it will form a triangle with the center of the bowl as the apex and two of the balls centers delineating its base. This apex will always form an angle of 360° number of balls. Either of the base angles will thus always form an angle of [180-(360/n)] /2. That is where the a and b from the formula above come from.
Their use is derived in this way. Looking at one of these triangles as we did above, the distance from the center of the bowl to the center of either ball will be opposite one of the base angles and two of the ball radius' will form the base opposite the apex.
Using the law of sines;
d /sin[(180 - 360/n)/2] = 2r / sin(360/n);
d = {2rsin[(180 - 360/n)/2]} / sin(360/n);
Now, remember that the radius of the bowl equals the radius of a ball plus the hypotenuse of the triangle formed with a horizontal d and a vertical r.
That hypotenuse from the center top of the bowl to the center of one of the balls is then;
√d² + r²;
(instead of typing all of those angle formulas again I will revert to a and b as shown above)
d = 2rsina/sinb; d² = 4r²sin²a / sin²b
The radius of the Bowl, R, is now just;
R = r + √[(4r²sin²a / sin²b) + r²]
Taking out the r² from the radical sign and simplifying yields;
R = r + r√[(4sin²a / sin²b) + 1];
R = r( 1 + √[(4sin²a / sin²b) + 1];
I hope that explained it, just ask if something is not clear. I have done nothing here different from what was done above, but solved it in the general form.
It won't work for other problems. In other words only the number of balls can change and not any of the parameters such as the tops of the balls being even with the top of the bowl....
I am at an age where I have forgotten more than I remember, but I still pretend to know it all.
Offline
Pages: 1