Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2019-06-17 19:46:32
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Expanding Thue Morse sequence i layers of circles
By generating Thue Morses sequence in rings and study the natural numbers N (including 0) represented by radial binary combinations some geometrical properties emerges, such as:
* All odd integers will be arranged in a specific geometric order
* Even integers will be arranged in a specific geometric order
* The one complement will allays be an opposite radial combination where the two radial combinations together constitute a diagonal.
* The two complement for a radial combination can be found by symmetry.
The presentation got a lot of graphics so I can´t post it here but I put it up on my blog if someone cares to take a look.
Some symmetrical properties constructing the natural numbers using Thue Morse sequence
Offline
#2 2019-06-18 22:16:28
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
An example of symmetries regarding the set of odd numbers in a n=4 ring system (or universe - in the terms used in set theory). The two complement to an odd number represented by a binary radial combination will always be perpendicular.
An example of symmetries regarding odd numbers in a n=4 ring system (or universe - in the terms used in set theory). The two complement to an odd number represented by a binary radial combination will always be perpendicular.
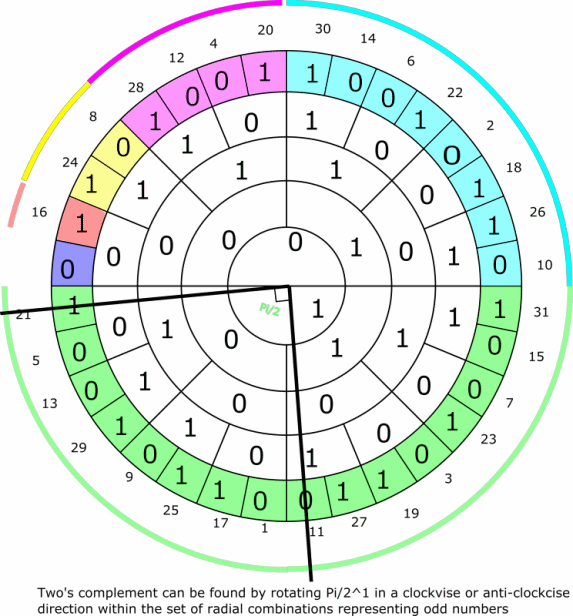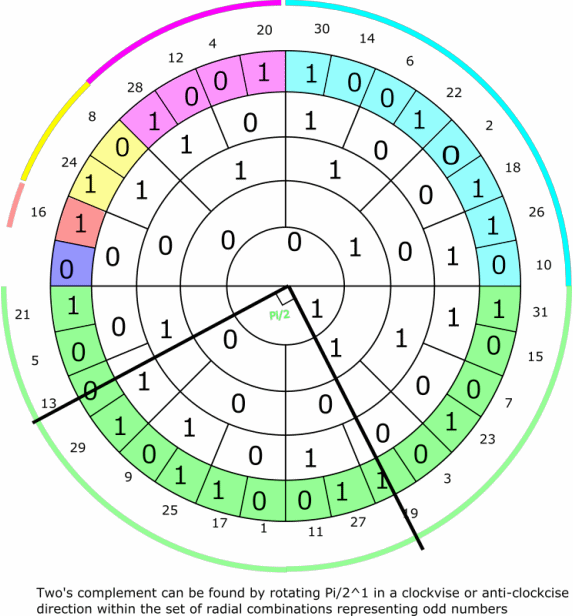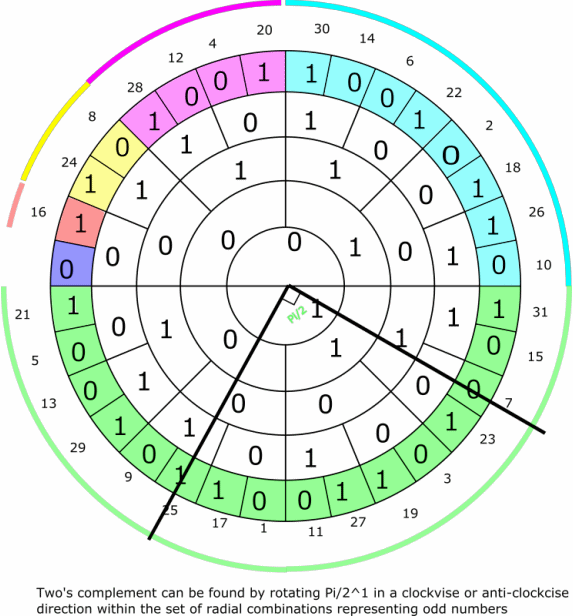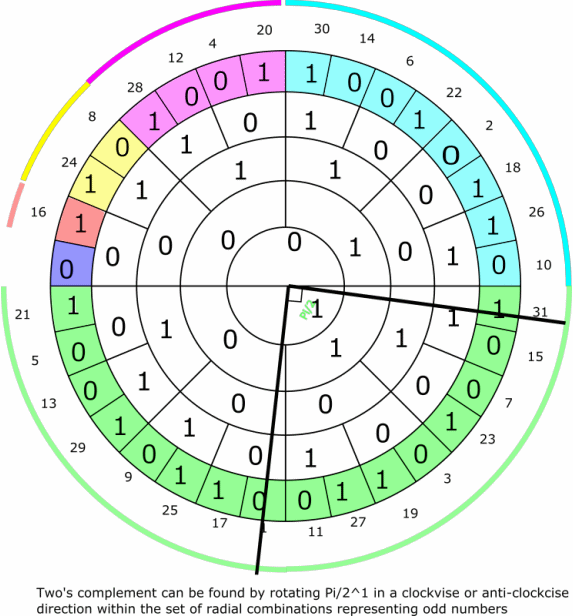
Last edited by Tudde (2019-06-18 23:03:02)
Offline
#3 2019-06-19 16:02:26
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
The two´s complement for the set of even integers represented by binary radial combinations in a n=4 ring system colored light blue (the sets are more formally defined in the presentation - see link above) can be found by rotating Pi/2^2=Pi/4 within the set - illustrated by the animation below.
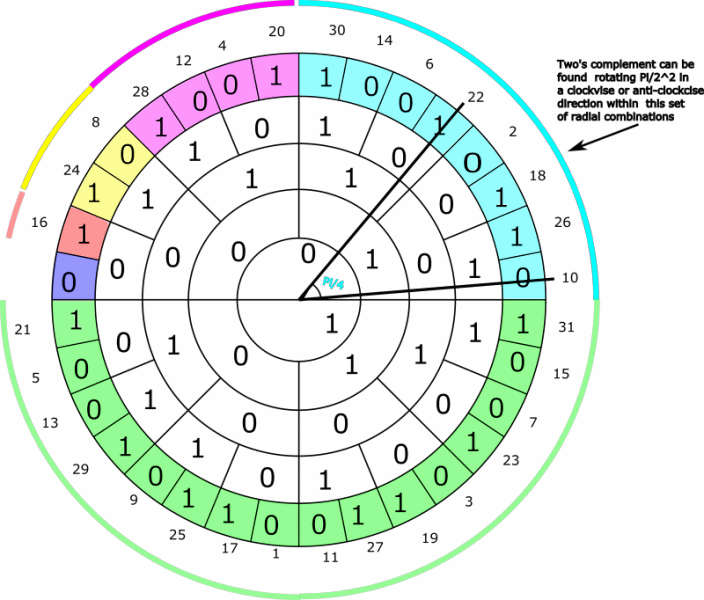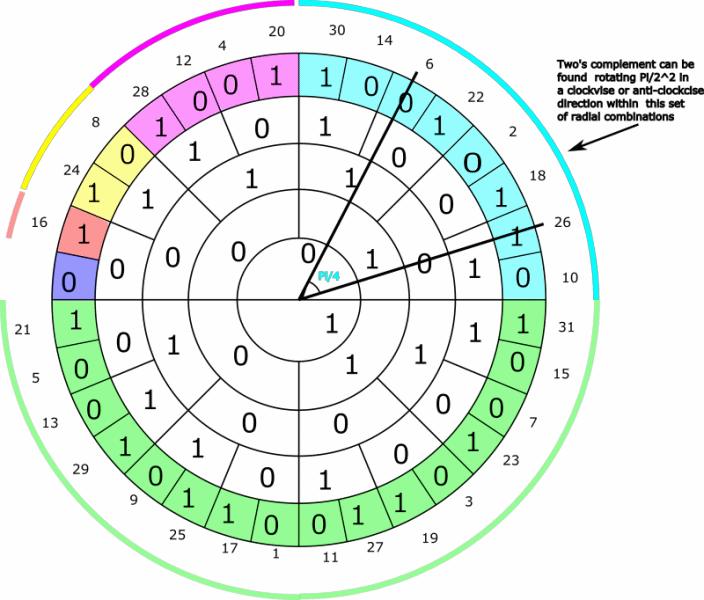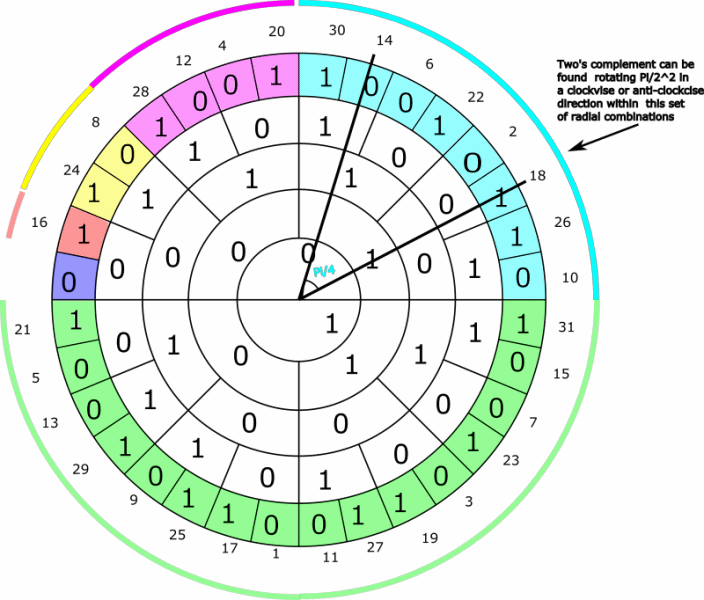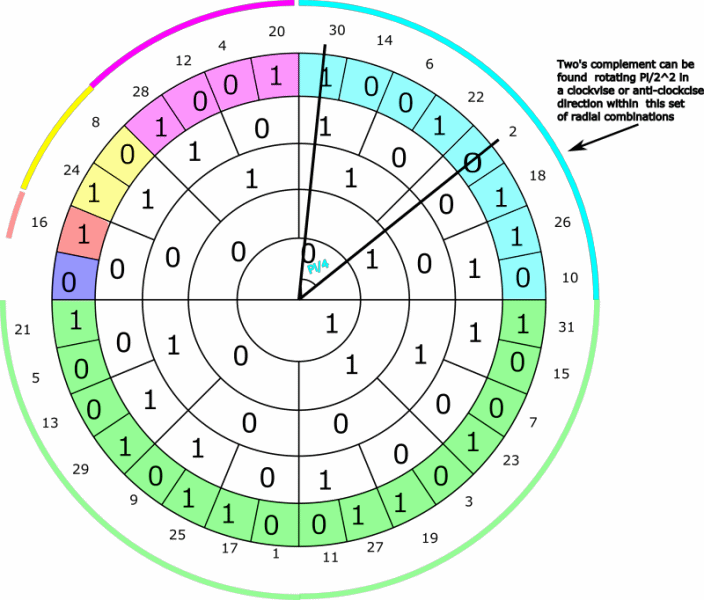
The two´s complement for the set of even integers represented by binary radial combinations colored pink can be found by rotating Pi/2^3=Pi/8 within the set - illustrated by the animation below:
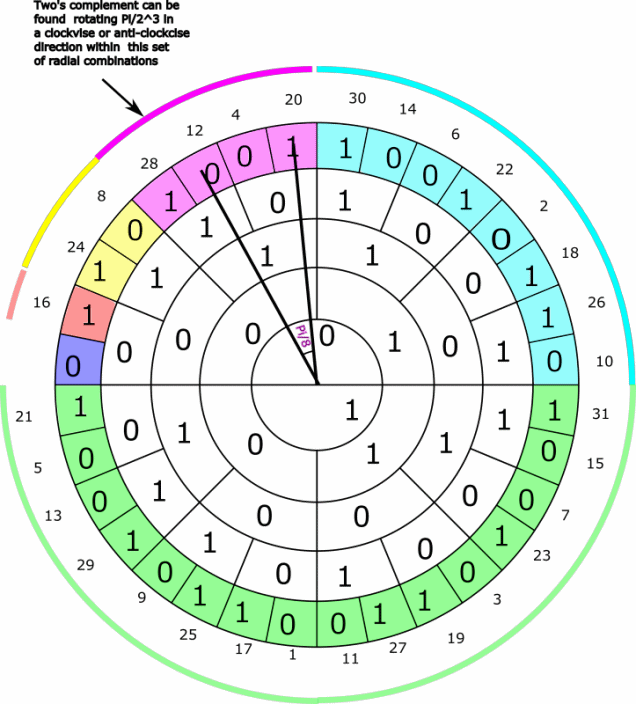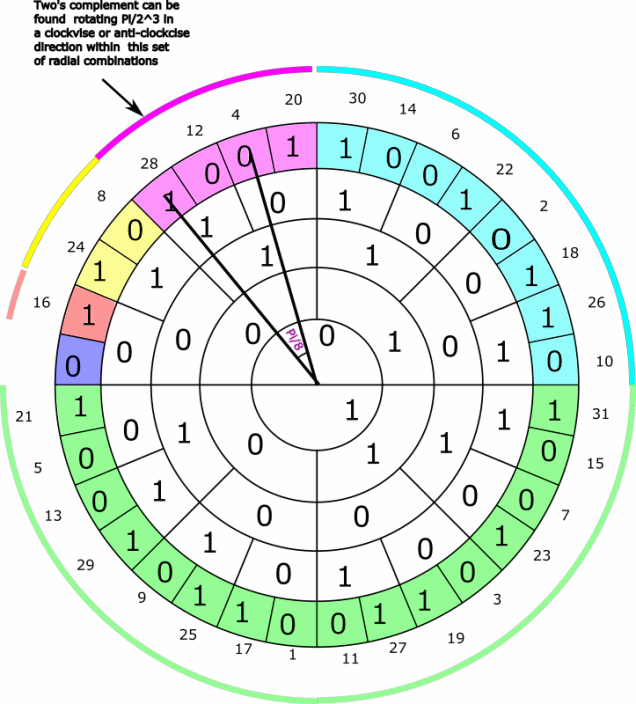
The two´s complement for the set of even integers represented by binary radial combinations colored yellow can be found by rotating Pi/2^4=Pi/16 , that is to say Pi/2*n within the set - illustrated below:
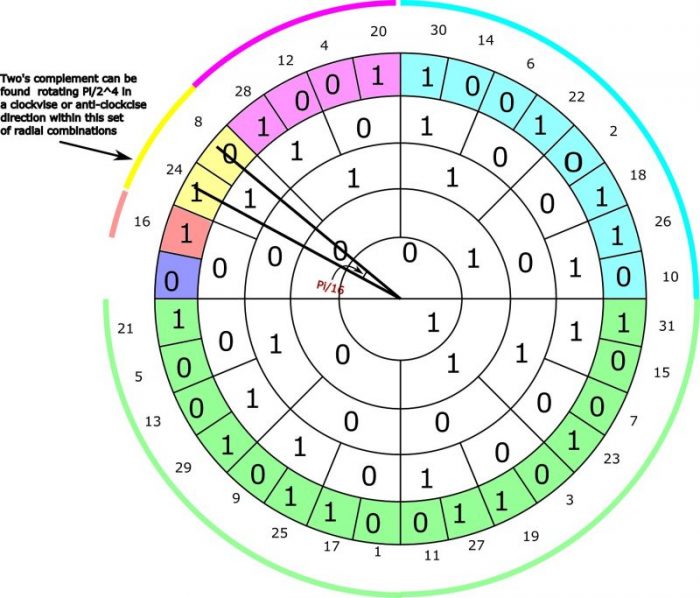
The binary radial combination represented by orange color only consist of one element and will have it self as twos complement
And lastly - the twos complement for the number 0 will result in a carry outside the system – sort of hitting the infinity wall for this universe and a loophole to the next universe (from n=4 to n=5 in the case above).
Above symmetries can be found in ring system n=0 ..... n=5 and can probably proven for all n by induction by generating the Thue Morse sequence in a L-system similar to the way that it can be proven that a given diagonal will consist of a radial combination and it's one complement (see the presentation)
Offline
#4 2019-06-20 16:18:07
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
t’s optional to use angle notations in finding the twos complement in the different sets. In the above example arbitrary radial combination for the two complement for the set of odd integers can be found 8 cells away from any radial combination in the last ring. The two complement in the next set going anticlockwise can be found 4 cells away. The general rule seems to be that the two complements can be found 2^(n-1) , 2^(n-2), 2^(n-3)…….2^(n-n), 0 cells away within the given set following the anticlockwise convention used above. This can probably be shown by some sort of induction proofs since it’s true for systems n=0 to n=5. As shown in the picture below:
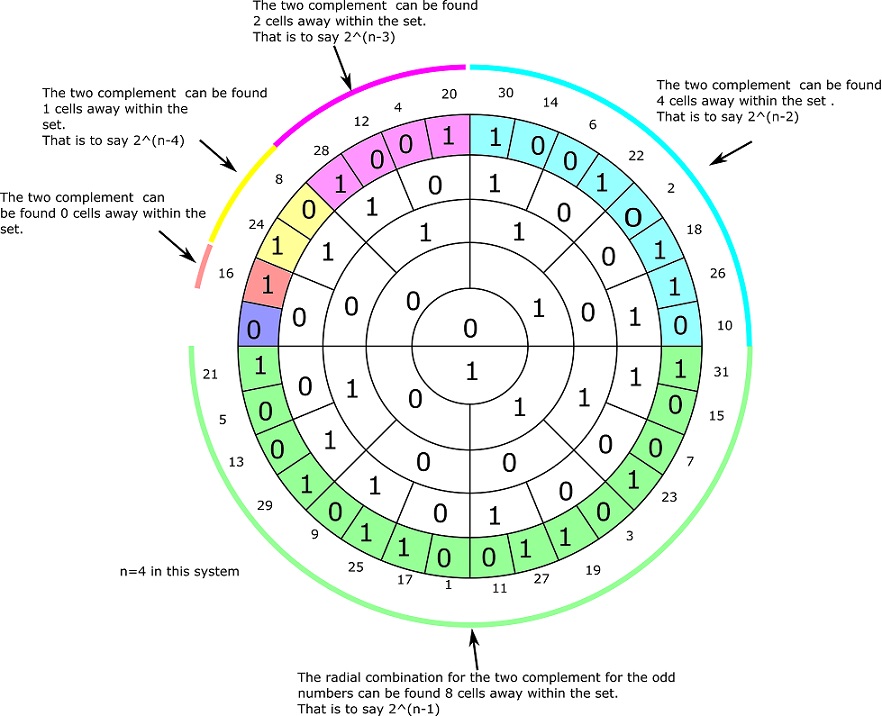
Offline
#5 2019-06-23 15:22:26
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
Any given diagonal will consist of two radial combinations that are the ones complement to each other as shown below. This is true for all radial combinations in a n=4 system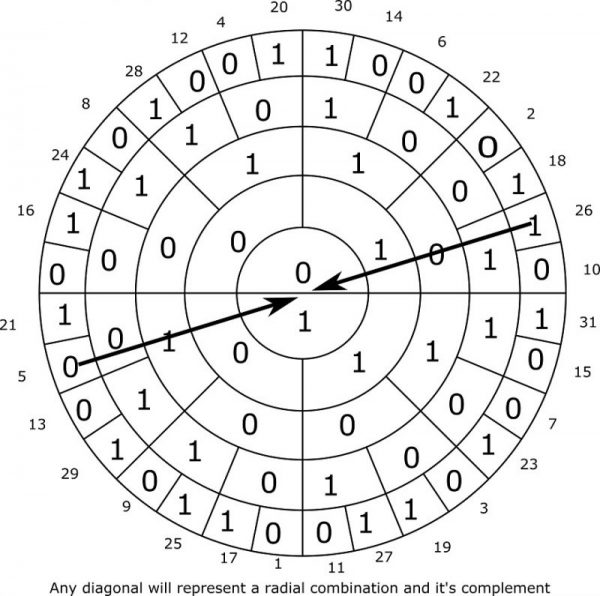
This can be generalized for a general n-system by induction as shown below:
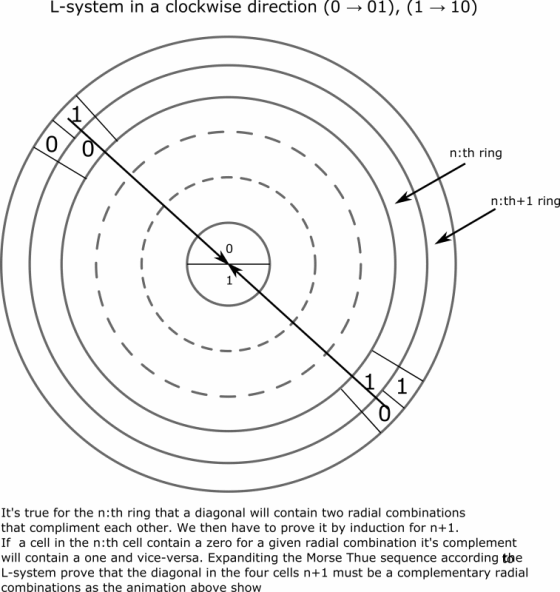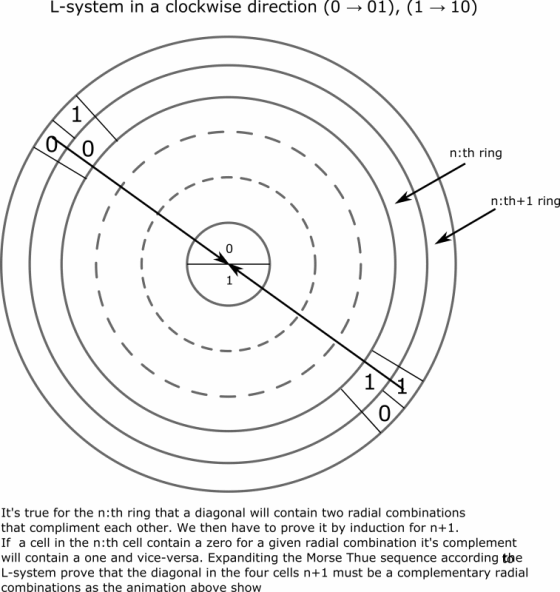
Last edited by Tudde (2019-06-23 15:27:10)
Offline
#6 2019-06-24 14:41:12
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
If we sum the radial combinations in each set defined as above in a system where n=4 we see that starting from the set of odd numbers going anticlockwise the sums adds up to 256, 128, 64, 32, 16 and 0 – see picture below. The general patterns for the sums in a n-system of the sets starting from the odd numbers going anticlockwise seems to be 2^(2n), (2^(2n-1), 2^(2n-2)…. 2^n and lastly 0 (the zero can alternatively be ignored if we exclude it from N). This can probably be proved as a general rule for all n by induction since its true for n=0 to n=5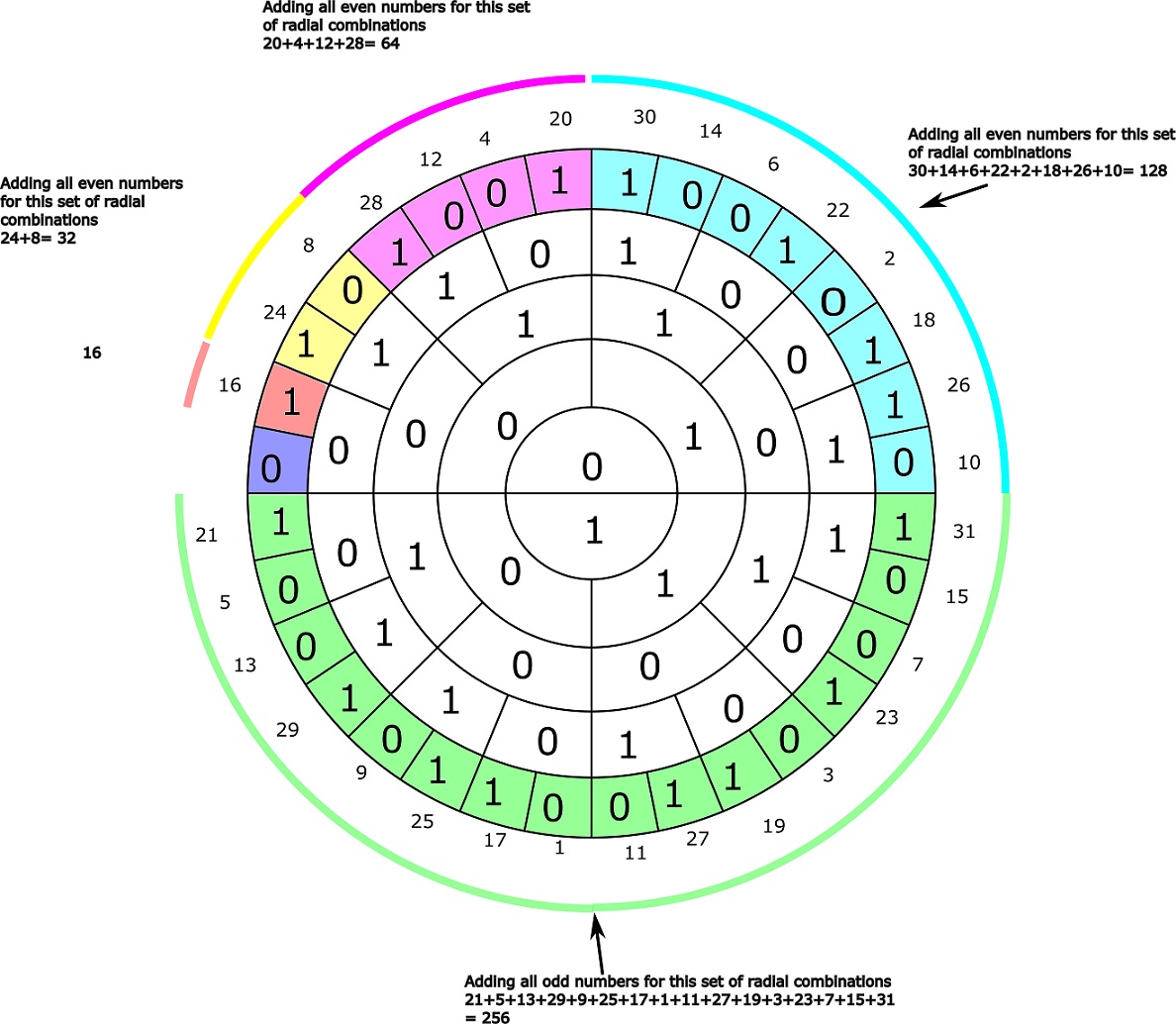
Offline
#7 2019-06-25 17:13:54
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
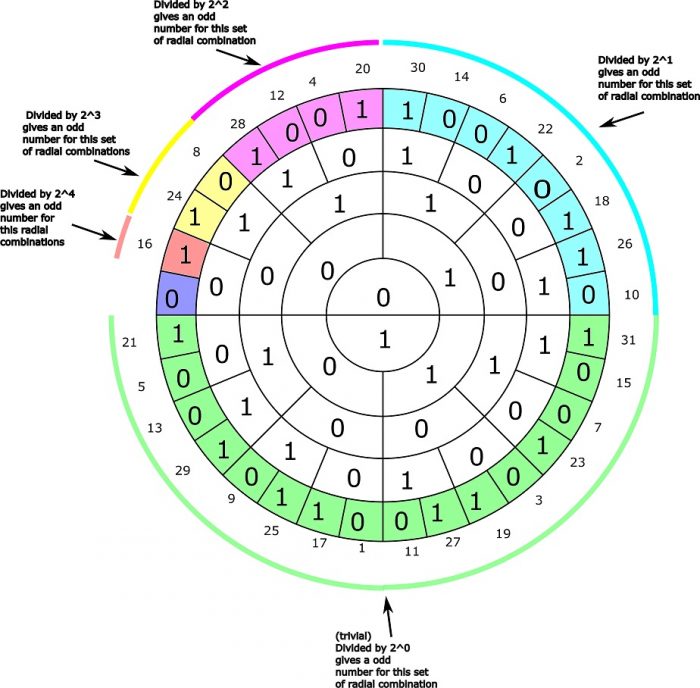
The radial combinations in each set of integers also show how “close” they are to be an odd number as shown below for a system where n=4. It can probably also be proven for an arbitrary n by some sort of induction proof since it’s s true for n=0 to n=5
Offline
#8 2019-06-29 04:20:31
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
The system can also be used as an alternative way to express boolean truth tables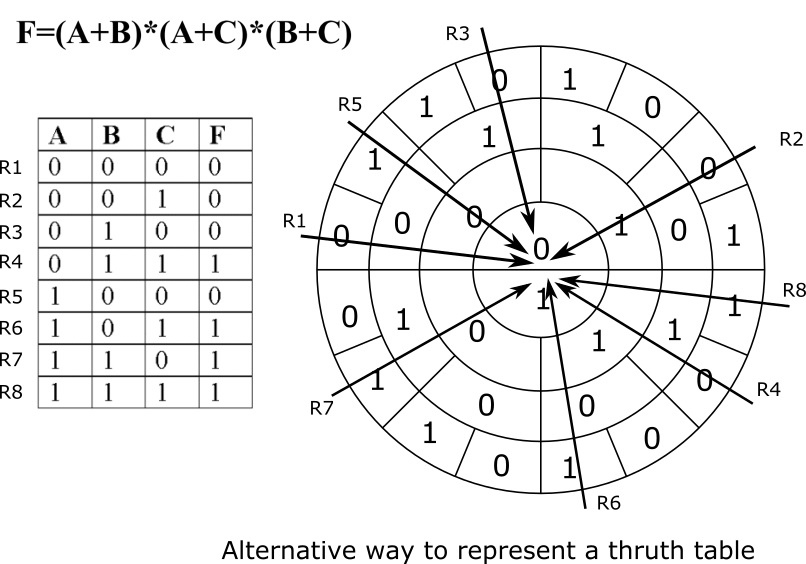
Offline
#9 2019-06-29 18:35:22
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
The remaining radial combinations represent the trythtable for the NOT-function: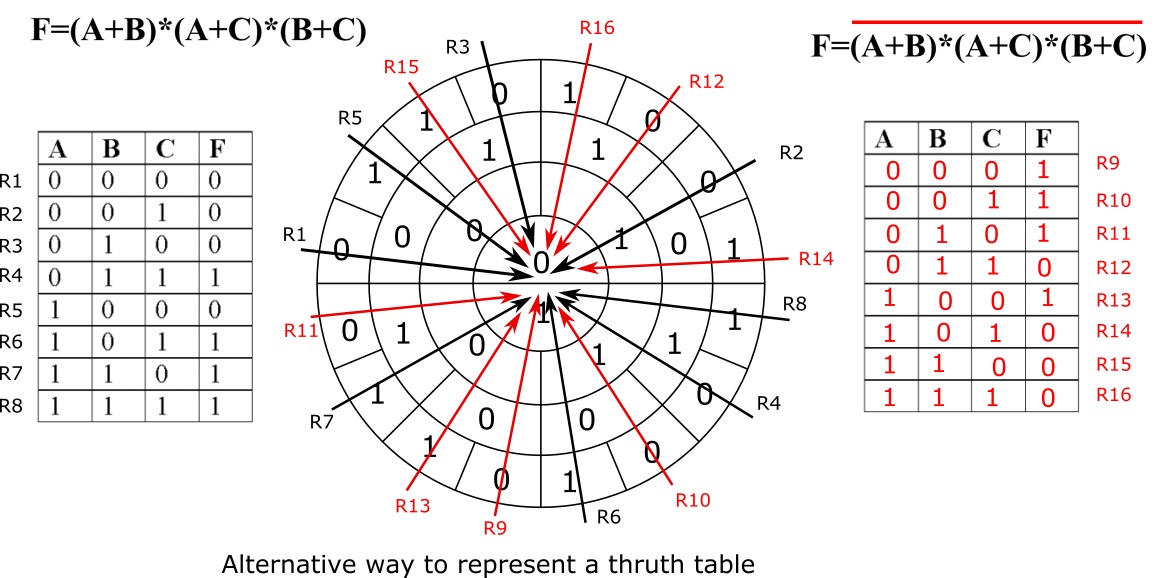
Offline
#10 2019-07-02 21:07:55
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
The system can also be used to do arithmetic. As in the animated example below where 9 is added to 12 giving the result 21. Subtraction can be done by finding the two complements according to the rules established above.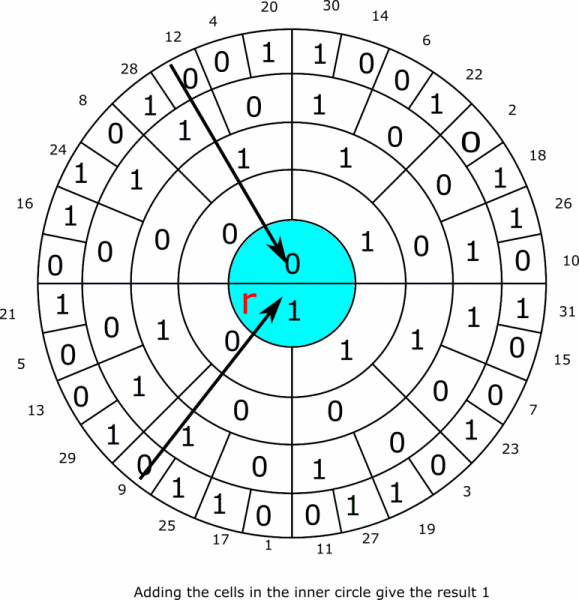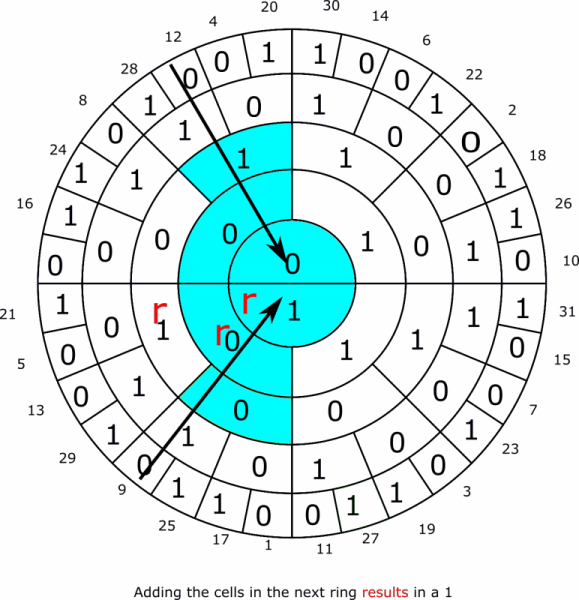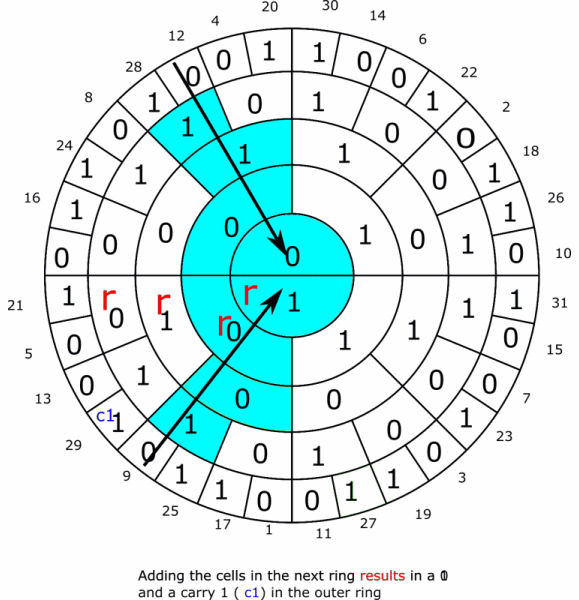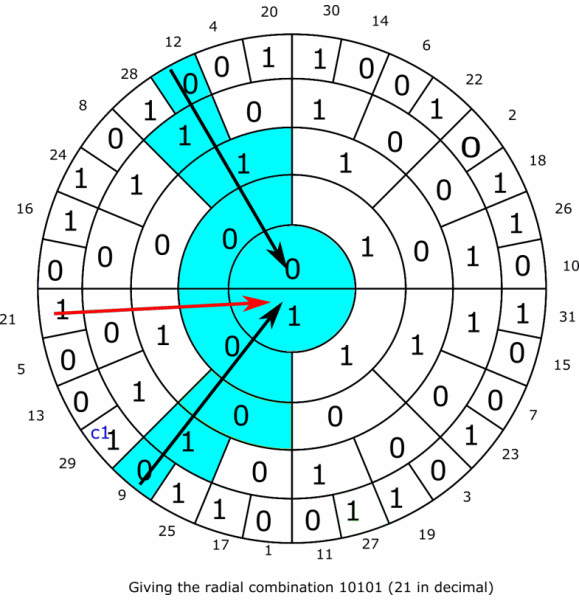
Offline
#11 2019-08-01 03:26:23
- Tudde
- Member
- Registered: 2019-06-17
- Posts: 11
Re: Expanding Thue Morse sequence i layers of circles
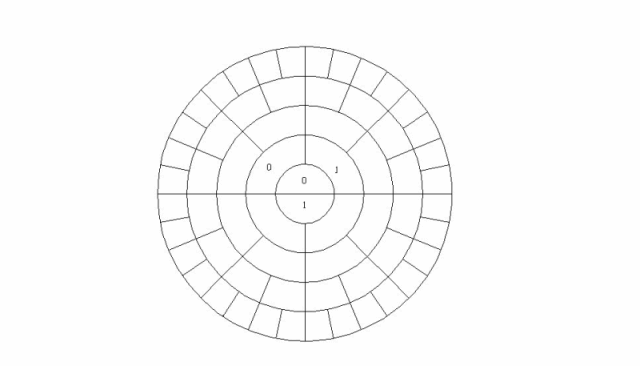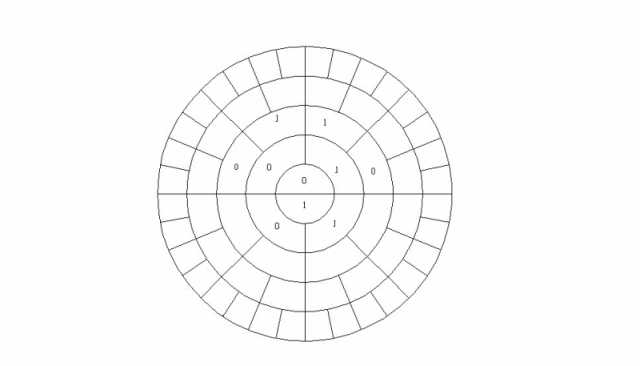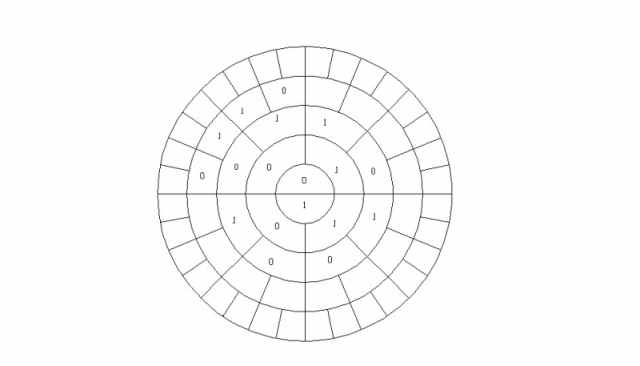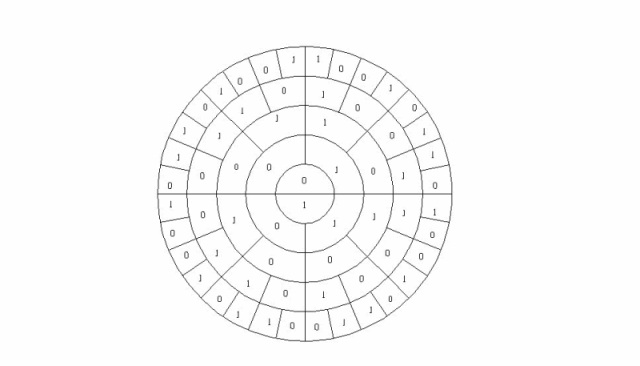
Generating the ring system is quite simple by expanding the Morse Thue sequence starting from the inner circle filling neighboring cells clockwise with 0 and a 1 by applying the L-system (0 → 01), (1 → 10) as shown in the animation below
The inner circle represent 2^0, the first ring 2^1, the next ring 2^2 and so on. Binary radial combinations can then be represented by the combinations of ones and zeros generating the numbers 0 to 31 in binary in the example above. At first the numbers might seem to be rather randomly displaced but, as shown above, there are some very interesting patterns and symmetries hiding in the way the natural numbers are arranged.
Offline