Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2017-03-24 16:00:49
- !nval!d_us3rnam3
- Member

- Registered: 2017-03-18
- Posts: 46
Tough question, need answer before tomorrow night. Thanks!
Let $\overline{PA}$ and $\overline{PC}$ be tangents from $P$ to a circle. Let $B$ and $D$ be points on the circle such that $B$, $D$, and $P$ are collinear. Prove that $AB \cdot CD = BC \cdot DA$.
I've already tried Power of a Point and similar triangles, but I can't seem to get anything to work. Can someone help me directly? By the way, don't post another link from this website, as I've probably checked that one already. Many thanks! ![]()
P.S. I need the answer before Saturday night.
"If we wanna be great, we can't just sit on our hands" - 2017 NFL Bears draft
Offline
#2 2017-03-25 01:37:55
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Tough question, need answer before tomorrow night. Thanks!
hi !nval!d_us3rnam3
Welcome to the forum.
Homework due again? ![]()
Backgound reading here:
http://www.mathisfunforum.com/viewtopic.php?id=22506
Hint: Use the angle between a chord and a tangent is equal to the angle made by the chord to show angle BDC = angle BCP and hence that triangles PCB and PDC are similar.
Do a similar thing for triangles PDA and PAB.
Also note that PA = PC.
Writing ratios for PB/PA should enable you to complete this.
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#3 2017-03-25 02:46:01
- !nval!d_us3rnam3
- Member

- Registered: 2017-03-18
- Posts: 46
Re: Tough question, need answer before tomorrow night. Thanks!
I've already proved similar triangles. Just need a little help going from there. Can you help me through the ratios? Most of the time I get the same result as using Power of a Point.
I'll be on this forum fairly actively if I need any homework help.
"If we wanna be great, we can't just sit on our hands" - 2017 NFL Bears draft
Offline
#4 2017-03-25 05:35:35
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Tough question, need answer before tomorrow night. Thanks!
When I'm working with similar triangles I write equivalent points in the same order, to make it easier to generate ratios; thus:
PDA
PAB
So PB/PA involves taking the first and third letters from the bottom three and the first and third from the top three. I've underlined the ones I mean.
So I can set that equal to another ratio taken in the same way. As I want DA and AB in the final answer, it makes sense to take them; so:
So that's half way there.
Now your turn.
Repeat for the other pair of similar triangles, again looking to make PB/PA. Except there's no PA this time. No worries; because the two tangents are equal, so you can use PB/PC.
Bob
ps. I've never heard of "power of a point". Would you care to explain when you get time?
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline
#5 2017-03-25 06:00:15
- !nval!d_us3rnam3
- Member

- Registered: 2017-03-18
- Posts: 46
Re: Tough question, need answer before tomorrow night. Thanks!
Power of a point, in this diagram, looks like PA^2 = PD*PB = PC^2. 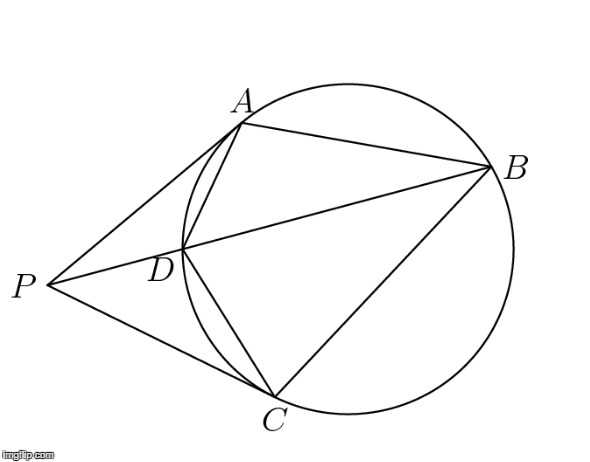
"If we wanna be great, we can't just sit on our hands" - 2017 NFL Bears draft
Offline
#6 2017-03-25 20:56:21
- Bob
- Administrator

- Registered: 2010-06-20
- Posts: 10,808
Re: Tough question, need answer before tomorrow night. Thanks!
My thanks, !nval!d_us3rnam3
I've never heard it called that but, as you will see from this link, I did know this:
http://www.mathisfunforum.com/viewtopic … 92#p368592
Bob
Children are not defined by school ...........The Fonz
You cannot teach a man anything; you can only help him find it within himself..........Galileo Galilei
Sometimes I deliberately make mistakes, just to test you! …………….Bob ![]()
Offline