Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2013-10-25 11:41:55
- mathstudent2000
- Member
- Registered: 2013-07-26
- Posts: 79
amc problems
1. A cube is sliced with one straight slice which passes through two opposite edges. The result is two solids, as shown. The area of the largest face on one of these two solids is 242\sqrt {2} square units. What was the exact surface area of the original cube?
2. A rectangle contains two circles of radius 6 that are each tangent to the rectangle in exactly 3 points. If the distance between the centers of the circles is 10, what is the area of the rectangle?
3. The rectangle below has height 8 and width 9. What value of k would make the shaded triangle's area 12\frac12% of the rectangle's area?
4. A 4" by 6" by 8" rectangular solid is cut by slicing through the midpoint of three adjacent edges. What is the number of inches in the sum of the lengths of the edges of the tetrahedron that is cut?
5. A cube of volume 27 has 1 x 1 square holes drilled through the center of each face and passing through the center of the cube. What is the volume of the figure that remains?
6. The circle is inscribed in a square with sides 8 cm. What is the area of the shaded part in square centimeters? Express your answer in terms of \pi.
Genius is one percent inspiration and ninety-nine percent perspiration
Offline
#2 2013-10-25 16:34:28
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: amc problems
Hi;
5) I am getting that 7 1 x 1 cubes are removed so the resulting volume is 20
Where are the drawings? For instance #6, which area do you want?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2013-10-27 15:26:57
- mathstudent2000
- Member
- Registered: 2013-07-26
- Posts: 79
Re: amc problems
the picture is here: http://classroom.artofproblemsolving.com/latex/e/4/4/e44183c89cddb01c6e653eb0a08526a673fb8717.png
Genius is one percent inspiration and ninety-nine percent perspiration
Offline
#4 2013-10-27 15:30:16
- mathstudent2000
- Member
- Registered: 2013-07-26
- Posts: 79
Re: amc problems
got another question: The triangle ABC shown is a right triangle. The semicircles have the sides of the triangle as diameters. The areas of two of the semicircles are shown. What is the area of the third semicircle?
https://www.google.com/search?tbs=sbi:A … tDeOQ2gUs#
the image is the one in the search
Genius is one percent inspiration and ninety-nine percent perspiration
Offline
#5 2013-10-27 15:35:06
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: amc problems
Hi;
That link gets me to google's front page?
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#6 2013-10-27 22:06:26
- Nehushtan
- Member

- Registered: 2013-03-09
- Posts: 957
Re: amc problems
I get the following thumbnail but I cant open it on the Google page.
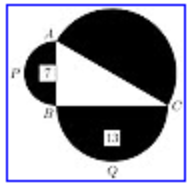
Use Pythagorass theorem and this formula:
where d is semicircle diameter / triangle side and A and is semicircle area. Thus
Hence the area of the third semicircle is 20.
240 books currently added on Goodreads
Offline
#7 2013-11-07 12:41:37
- mathstudent2000
- Member
- Registered: 2013-07-26
- Posts: 79
Re: amc problems
i'm pretty much sure it gets to the main pic
Genius is one percent inspiration and ninety-nine percent perspiration
Offline
#8 2013-11-07 13:26:11
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: amc problems
Hi;
6) 32 pi - 32
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#10 2019-07-29 15:26:43
- Monox D. I-Fly
- Member

- From: Indonesia
- Registered: 2015-12-02
- Posts: 2,000
Re: amc problems
4. A 4" by 6" by 8" rectangular solid is cut by slicing through the midpoint of three adjacent edges. What is the number of inches in the sum of the lengths of the edges of the tetrahedron that is cut?
I got
. Am I doing this right?Actually I never watch Star Wars and not interested in it anyway, but I choose a Yoda card as my avatar in honor of our great friend bobbym who has passed away.
May his adventurous soul rest in peace at heaven.
Offline
Pages: 1