Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#1 2010-09-11 10:58:57
- dude
- Member
- Registered: 2010-09-11
- Posts: 7
Need volume of hole removed from hollow cylinder with 5" thick wall
I also want to know how to work this problem.
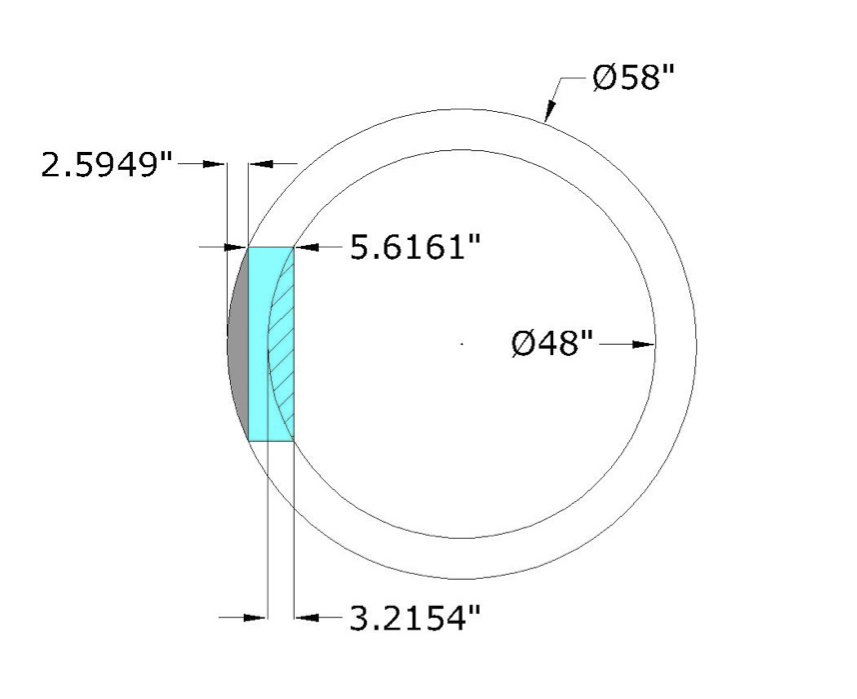
I have a vertical right cylinder that has an inner diameter of 48" and an out diameter of 58" inches. I am going to cut a hole, 24" in diameter through a place in the wall. I need to know how to solve for the removed volume exactly. I am sure after many hours of trying to break this down by geometric shape after shape that integrating may be my only hope. I am not very strong in that area since I am 13 years removed from Cal 1-3 and D.E.
Any help is greatly appreciated.
I have attached a photo to help illustrate my problem. This is just a photo I found while searching for a quest to answer my problem.
Offline
#2 2010-09-11 17:22:34
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Hi dude;
Welcome to the forum! I don't have anything more than a hunch based on some crude drawings. But let me the first to conjecture that the removed volume is:
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#3 2010-09-12 00:28:00
- dude
- Member
- Registered: 2010-09-11
- Posts: 7
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Hey BobbyM. Thanks for replying. That answer is incorrect. You used PI * r^2 * h => PI * 144 * 5 => 720 PI
That does not account for the curved surfaces which makes this problem a real pain in the butt.
I have tried breaking it down, via top view, into geometric shapes and no luck.
The problem is that although it looks like two domes are included in the attached photo, they are not domes.
Offline
#4 2010-09-12 04:56:33
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Hi dude;
Yes, my 5 is incorrect. I also assumed the two curved areas were equal.
Okay, I have that too. I can compute the area's in your 2D drawing ( the curved parts ) drawing easy enough.
There are formulas to compute the volumes of those caps as they are called. Check this out:
http://mathworld.wolfram.com/SphericalSegment.html
I do not think you will require integration.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#5 2010-09-12 06:27:53
- dude
- Member
- Registered: 2010-09-11
- Posts: 7
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Hi dude;
Yes, my 5 is incorrect. I also assumed the two curved areas were equal.
Okay, I have that too. I can compute the area's in your 2D drawing ( the curved parts ) drawing easy enough.
There are formulas to compute the volumes of those caps as they are called. Check this out:
http://mathworld.wolfram.com/SphericalSegment.html
I do not think you will require integration.
I call them domes but they are not. Notice I have a cylinder and those equations are fora sphere. No problem to calculate volume for domes cut from a sphere. Much different on a cylinder wall because the top view cross section is a bit misleading. Remember, I am cutting a circular hole through the cylinder wall.
Offline
#6 2010-09-13 15:17:22
- dude
- Member
- Registered: 2010-09-11
- Posts: 7
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
I will be posting the answer to this very soon. It's a heck of a mess. Get your hp48gx ready.
Offline
#7 2010-09-13 15:18:13
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Hi dude;
Let's see it. Who cares about the mess.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#8 2010-09-14 13:47:41
- dude
- Member
- Registered: 2010-09-11
- Posts: 7
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Letbme get the triple integral worked outvso I can post an exact method.
Offline
#9 2010-09-14 15:45:31
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Hi dude;
Okay. That's fine. I'll wait.
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#10 2010-11-13 16:46:25
- Fruityloop
- Member
- Registered: 2009-05-18
- Posts: 143
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
This is a difficult problem, but I think I have come up with the answer (hopefully).
You have a smaller cylinder intersecting a larger cylinder from the side.
Imagine that you have a 48" diameter cylinder and also a 58" diameter cylinder.
Imagine that you have a 24" diameter cylinder intersecting both.
Now, in order to find the volume of removed material all you have to do
is subtract the volume of intersection with the 48" cylinder from the
volume of intersection with the 58" cylinder. This all seems simple and
clear enough but how does one go about finding this?
Well, if you imagine the 24" cylinder intersecting the 58" cylinder you can
imagine that there will be a normal cylinder with a 'cap' on top.
The difficulty lies in finding the volume of this 'cap'.
The volume can be imagined as a rectangle moving through the 'cap'.
It's a bit hard to visualize but we need both the width and height
of the rectangle.
For the 24" cylinder looking down from above we have the relation
In this case, the x will serve as one of the sides of the rectangle.
For the 58" cylinder we have the relation
The height of the rectangle will be the part of h which is part of the
'cap' above the cylinder which is above 26.40075756.
We need the formula for the rectangle in terms of y since we will
be integrating with respect to y, so we end up with
for the area of the rectangle.
The integral will be from 0 to 12 and will be only 1/4 of the volume.
So the volume is equal to
Can anybody here integrate this?
I don't know how to integrate this so I cheated and used a computer program.
Now this is only the 'cap' so we need to add this to the cylinder
which is
So the total volume is
Now we do the same thing with the smaller cylinder
Total volume is
So the volume of removed material is
This is close to Bobbym's estimate of
Last edited by Fruityloop (2010-11-13 17:16:43)
Offline
#11 2010-11-13 19:15:59
- bobbym
- bumpkin

- From: Bumpkinland
- Registered: 2009-04-12
- Posts: 109,606
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Hi Fruityloop;
This is close to Bobbym's estimate of 2261.946711
bobbym's estimates are doodly doo! Hope that was not too strong a wording. All that numerical analysis has rotted his brain, yesterday I caught him bounding 7 * 13. He said it was greater than 90 but less than 100.
I do not think we will have much luck with an analytical answer for that integral. You were right to use a program on it. Nice work with the volume problem above!
In mathematics, you don't understand things. You just get used to them.
If it ain't broke, fix it until it is.
Always satisfy the Prime Directive of getting the right answer above all else.
Offline
#12 2010-11-14 01:18:41
- dude
- Member
- Registered: 2010-09-11
- Posts: 7
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
Fruityloop got it! That's the answer. Now workmit if your hole (24") was tapered say 1" inward all around.
Offline
#13 2010-11-14 15:20:02
- dude
- Member
- Registered: 2010-09-11
- Posts: 7
Re: Need volume of hole removed from hollow cylinder with 5" thick wall
PS I had to use my Hp48GX to integrate because they were tough. I'll finish the writeup soon and post a link. I have a hand sketch to accompany.
Thatsva tough one for sure.
Offline