Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#176 Puzzles and Games » Cute little problem I saw on another site » 2010-03-19 23:45:06
- JaneFairfax
- Replies: 3
#177 Re: Help Me ! » Lotto combinations » 2010-03-19 01:32:56
Consider how many ways there are of having more than 3 numbers in the same row.
(1) All 6 numbers are in the same row.
(2) 5 of the numbers are in the same row and the last number is in another row.
(3) 4 of the numbers are in the same row and the other 2 numbers are in another row (or rows).
Case (1): If the 6 numbers are in the first row, there are ways of choosing them. If they are in a row other than the first, then there are ways of choosing them in that row; as there are four possible non-first rows, there are 4 × 210 = 840 ways altogether of choosing them this way. Hence the total number of possibilities for Case (1) is 84 + 840 = 924.
Case (2): If the 5 numbers are in the first row, there are
ways of choosing them, leaving 40 possibilities for the sixth number; so there are 40 × 126 = 5040 ways of choosing the numbers this way. If the 5 numbers are in a row other than the first, then there are ways of choosing them, leaving 39 possibilities for the sixth number; so there are 39 × 1008 = 39312 ways of choosing the numbers this way. Hence the total number of possibilities for Case (2) is 5040 + 39312 = 44352.Case (3):
(i) Suppose the 4 numbers in a row are in the first row. There are
(ii) Suppose the 4 numbers in a row are not in the first row. Then there are
ways of choosing these 4 numbers. Now consider the other two numbers. They can be: (a) both in the first row, (b) both in the same row but not the first, or (c) in different rows. For (a), . For (b), . For (c), if one of the numbers is the first row, 9 × (3 × 10) = 270, otherwise 3 × 10 × 10 = 300, giving 270 + 300 = 570. So there are 36 + 135 + 570 = 741 ways of choosing the last 2 numbers, and hence the total number of possibilities for this subcase is 840 × 741 = 622440.Therefore, the number of possibilities for Case (3) is 98280 + 622440 = 720720.
Thus, the number of possible combinations in which at least four numbers are in the same row is 924 + 44352 + 720720 = 765996.
And the answer to your question is
#178 Re: Puzzles and Games » Chess (Flash Version) » 2010-03-18 03:16:26
That is about as good as I can get it with limited computing power. A rewrite in Actionscript could give it 10x the speed and allow deeper thinking.
Well, for a start, you could teach your program
(1) not to move knights to the sides of the board unnecessarily (knights are more useful in the centre of the board, where they are more mobile)
(2) not to touch the a- and h-pawns until later in the game (the side pawns early on are better engaged in defending the more central pawns, which should be deployed to take control of the centre of the board as quickly as possible)
#179 Re: Puzzles and Games » Determine » 2010-03-17 16:31:57
#180 Re: Puzzles and Games » Find all solutions » 2010-03-17 15:35:50
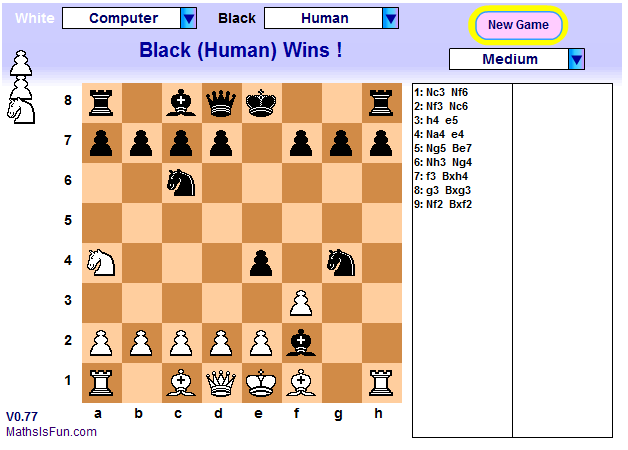
#181 Puzzles and Games » Chess (Flash Version) » 2010-03-17 13:59:49
- JaneFairfax
- Replies: 14
http://www.mathsisfun.com/games/chess.html
This program is really, really, really stupid. This was the game I just played against it.
#182 Re: Help Me ! » Angle between two vectors in the plane.. » 2010-03-17 06:50:35
Do you mean you want angles rotated clockwise to be negative and those rotated counterclockwise to be positive? Then try this formula:
This is computed using the cross product rather than the dot product. In your example (following your style in taking the downward y-direction as positive):
And the cross-product formula gives
While
and the angle with the first vector is
Welcome to the forum, mrfandus. ![]()
#184 Re: Help Me ! » Writting an Equation » 2010-03-12 04:41:43
Write an equation for:
Quadratic with only one zero at the vertex point (-9,0) that is everywhere negative.
I know bobbym has kindly helped you out here, but this is your second time here now. Are you actually putting any of your own effort into doing your own homework, or just waiting for nice people like bobbym to give you something for you to copy?
#185 Re: Help Me ! » bijective inverse function » 2010-03-06 01:10:54
Yes, thats all there is to it. ![]()
#186 Re: Help Me ! » Language » 2010-03-06 00:59:08
From my experience, Spanish is easy to learn. It is also very widely spoken, so it could come in handy. Therefore, Spanish would be my recommendation. ![]()
#187 Re: Puzzles and Games » What comes next in this sequence? » 2010-03-05 09:53:23
Very good! ![]()
#188 Puzzles and Games » What comes next in this sequence? » 2010-03-05 09:28:52
- JaneFairfax
- Replies: 7
01:05:27, 02:10:55, 03:16:22, 04:21:49, 05:27:16, 06:32:44, 07:38:11, 08:43:38, 09:49:05, 10:54:33, ___
Please use hide tags to hide your answer.
#189 Re: Jokes » funny video i did » 2010-03-05 09:16:31
I thought you waited too long before kicking the packet. I suggest shortening the video by cutting maybe the first ten seconds or so of it. Nice little video, by the way. ![]()
#190 Re: Help Me ! » bijective inverse function » 2010-03-05 09:07:43
Your proof of the injectiveness of is perfect.
There is no necessity to prove the converse, which is merely establishing that the inverse function is well defined. Still, if you want to prove it, use the fact that
is injective.To prove ontoness, take an
and find a such that . The obvious choice would be .#192 Re: Help Me ! » simplification of factorials? » 2010-03-03 10:58:16
it is so .... not straight-forward
Yes, it is. You just need to get used to the trick. ![]()
#193 Re: Help Me ! » simplification of factorials? » 2010-03-03 10:33:43
The inductive step should be
#194 Re: Help Me ! » Calculus II - Series/Sequences Questions » 2010-03-03 10:13:30
Equate imaginary parts to solve for each.
#195 Re: Exercises » Is this cool with you? » 2010-03-02 01:30:32
Theyre all wrong. Correct answer is
When k = −5 or 0, it still has 4 real roots (repeated roots count as two roots).
#196 Re: Help Me ! » Even or Odd or Constant function? » 2010-03-01 22:26:25
All of them.
#197 Re: Maths Is Fun - Suggestions and Comments » Spelling? » 2010-02-28 12:24:13
Jane: I think you can have a list of languages in preference order, so you could set en-GB as second.
What I mean is, use American English only for en-US browsers. For all other browsers, including non English-language browsers, use British English. Simple?
I'll throw in another yay for en-GB being correct.
![]()
#198 Re: Dark Discussions at Cafe Infinity » Frankly I am a little miffed. » 2010-02-28 01:10:01
I posted my own little rant at the other thread.
#199 Re: Maths Is Fun - Suggestions and Comments » Spelling? » 2010-02-28 01:06:52
I have my Firefox browser set to fr-FR (because I want to) and it is showing me the American spelling instead.
So I take it that American spelling is the default choice for non en-GB / en-AU browsers.
How about making it so that British spelling is the default choice for non en-US browsers? Wouldnt that be simpler? Hey? ![]()
#200 Re: Help Me ! » real analysis problem!! » 2010-02-27 03:51:47
Youre welcome. I just realized however that you posted this as a real-analysis problem, so it may be that you have to use calculus here. While Jensens inequality gives a quick solution without using calculus, it may not be what your teacher wants. Do check with your teacher on what is required for this problem. ![]()
