Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#176 Re: Help Me ! » Maximise ... » 2014-10-19 04:45:24
Hi bobbym.
Someone has asked the same question on another forum – I think you can answer it. ![]()
[list=*]
[*]http://www.artofproblemsolving.com/Foru … 6&t=610381[/*]
[/list]
#177 Re: Help Me ! » A question about limits » 2014-10-18 20:49:53
Well, let us assume at each step the original line is broken into fragments of equal length. After the first step we have 4 fragments of length 1/4, after the second we have 16 fragments of length 1/16, etc. Then we have
[list=*]
[*]
[/list]
Hence
[list=*]
[*]
[/list]
#183 Re: Help Me ! » Critical points problem: Differential equations » 2014-10-13 22:30:13
I think you mean dy/dt in the second equation. If you divide the second by the first you should get
[list=*]
[*]
[/list]
eliminating the parameter t.
#185 Re: Help Me ! » Logarithm which goes first? » 2014-10-10 07:57:51
There seems to be some confusion here. What Whizzies means is that (excluding complex numbers) log(y) is only defined for y > 0. The problem involves log(x+3), so y = x+3. It is fine for x = −1; it is the y that needs to be > 0.
#186 Re: Help Me ! » Logarithm which goes first? » 2014-10-10 04:32:43
You’ve got as far as
[list=*]
[*]
[/list]
Now just solve it for x. ![]()
#187 Re: Help Me ! » mathematics » 2014-10-09 06:13:05
[list=*]
[*]
[/list]
#189 Re: Help Me ! » Maximise ... » 2014-10-08 22:07:26
Why?
It would make no sense for the maximum to be biased towards either x, or y, or z. So It ought to be when they are equal.
That was what I thought as well until I found this: ![]()
That might be the maximum but I don’t know how prove it yet (with or without Langrangian multipliers). ![]()
#190 Re: Dark Discussions at Cafe Infinity » Princeton, Harvard and MIT? » 2014-10-08 05:03:11
I almost got half right.
You did better than over 50% of students from Princeton, Harvard and MIT. ![]()
#191 Re: Dark Discussions at Cafe Infinity » Princeton, Harvard and MIT? » 2014-10-08 04:26:41
Well, they’re not that difficult. ![]()
#1. What is CD in Roman numerals?
#2. The cube of a number is that number multiplied by itself three times – true or false?
#3. What is the pseudonym of the writer Mark Twain?
#192 Re: Help Me ! » Sequence Limit Proof » 2014-10-08 04:13:33
You’re welcome. ![]()
As I said, problems of this kind often demand a lot of ingenuity from the solver, but practice and experience can help a lot. Don’t worry if you can’t come up with such things on the spot – I certainly didn’t for this one! I had to think hard about it for a while. While thinking about it, I realized that the 1 was going to be a problem if I was going to use the triangle inequality, so I tried splitting the 1 into the terms of the sum – and it worked. I mean, it might not have worked and then I would have to start again from the beginning, but fortunately it did. So yeah – practice, practice, practice. ![]()
#193 Re: Dark Discussions at Cafe Infinity » Princeton, Harvard and MIT? » 2014-10-08 04:04:58
Perhaps those students of Harvard, Princeton and MIT would also be interested in the following questions? ![]()
[list=1]
[*]What is CD in Roman numerals?
[/*]
[*]The cube of a number is that number multiplied by itself three times – true or false?
[/*]
[*]What is the pseudonym of the writer Mark Twain?[/*]
[/list]
#194 Re: Help Me ! » Sequence Limit Proof » 2014-10-08 01:01:50
If you define N as the minimum of two values, both values must be positive. However for limit problems it’s more usual to define N as the maximum of two values, not minimum.
For problems of this kind you often have to be imaginative. And for this problem I think the key is this:
[list=*]
[*]
[/list]
Hence:
[list=*]
[*]
[/list]
Now for r = 1, …, n, we have
[list=*]
[*]
[/list]
Thus:
[list=*]
[*]
[/list]So given you can take .
#195 Re: Help Me ! » Sequence Limit Proof » 2014-10-07 01:39:00
This step
is not valid. Epsilon might be less than or equal to 2.
I don’t really know how you could go about choosing a suitable N for this problem. Let me think about it. ![]()
#196 Re: Maths Is Fun - Suggestions and Comments » Emoticons - Smilie Expressions » 2014-10-07 01:34:42
Any plans to make the smilies clickable again? ![]()
#198 Re: Help Me ! » Discrete Mathematics - Reduction / Deduction! » 2014-10-06 02:16:55
So the given implication is correct.
#199 Re: Help Me ! » Differential equations problem » 2014-10-01 21:25:31
So instead of x' you have to type x^{\prime}?
[list=*]
[*]
[/list]
#200 Re: Help Me ! » Differential equations problem » 2014-10-01 20:53:21
[list=*]
[*]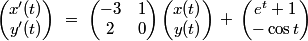 [/*]
[/*]
[/list]
Off-topic: Why isn’t LaTeX working? ![]()