Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#76 Re: Help Me ! » need a geometry reminder » 2008-09-11 10:21:17
thanks for the replies, and the interesting discussion! ![]()
fortunately I found a relation between L1, L2 and L3, but only if you consider them as vectors.
consider the points A,B,C and Q and the scaler k defined as below: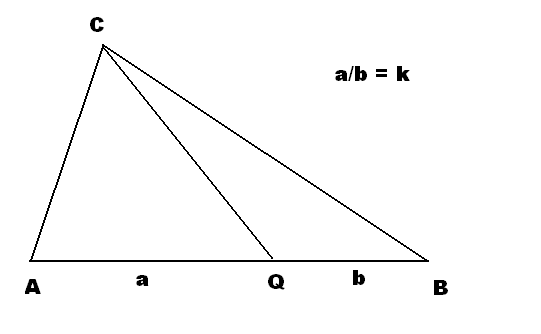
obviously,,
and
and observe:
so
thus multiplying equation (2) by k and adding the result to equation (1), and solving for (C-Q) yields
not exactly the problem i asked initially, but it gives me the sort of relation i wanted.
#77 Re: Help Me ! » need a geometry reminder » 2008-09-09 23:37:12
Congrats on 3000 posts! ![]()
But I'm not sure I follow you. You mean draw a line straight down from the upper left vertex, and extend the base line leftward to meet it?
#78 Help Me ! » Events, Sample spaces, Sets and boolean logic » 2008-09-09 09:20:12
- mikau
- Replies: 1
So my discrete math book, in the section on sets suddenly begins using the terms 'event' and 'sample space' without defining them.
I think I can guess the idea. It sounds like an 'event' is a set of possible occurrences, and an occurrence is thus an instance of an event. Or an element of an event.
What a sample space is i'm not sure. I seem to recall that term from probability.
Anyway, so the impression I get is that we have a kind of event, such as the event of a building fire, and the event of building collapse. And we can therefore consider these as sets and take the intersection, to 'AND' both events together, to get the event that a building is on fire and collapses.
Moreover, we can take the union to 'OR' both events together, to get the event that either the building is on fire or collapses. Lastly, we can negate or 'NOT' an event by using the 'without' set operation, for instance, the event in which the building is on fire, without the collapsing event
so it looks like you can construct logical statements about events using intersection, union, and 'without' (or complement) for AND, OR, and NOT.
So here's two problems, please let me know if my approach is correct:
Let A B C be events of some sample space Q. Write in symbols:
(1) The event that at least two of the three events occurs
(2) The event that at most one of the three events occurs
(1), we have that either 2 of the events occur, or all 3,
two events means (A and B) or (A and C) or (B and C) or (A and B and C)
the last is redundant though it shouldn't hurt anything,
so for set operations we replace 'and' with 'intersection' and 'or' with 'union' and we should get a valid answer, right?
(2) only one most occur at a time, so we have A and not (B or C) or B and not (A or C) or C and not (A or B)
we can replace 'and' and 'or' with 'intersects' and 'union' and not (in this case) with 'without'.
Is this the correct approach to these problems?
If so, this relation between set theory and boolean algebra is pretty sweet.
#79 Re: Help Me ! » Least common multiple of every natural number? :O » 2008-09-09 08:27:27
Thanks, mathsyperson!
That makes sense. On the otherhand, my alternate suggestion for how to build an infinite intersection also makes sense. Tricky thing about the infinite, so often two conflicting propositions seem correct.
I'll have to think about this for a while. Hmm.. maybe Anthony R. Brown can clear it up for me. ![]()
![]()
#80 Help Me ! » Least common multiple of every natural number? :O » 2008-09-09 07:20:26
- mikau
- Replies: 3
okay, so I proved in one of my homework problems that the intersection of the sets
{0, a, 2a, 3a, ... } and {0, b, 2b, 3b, ... } is { 0, u, 2u, 3u, ...} where u = LCM of a and b.
but in a later homework problem, it says:
let A[sub]n[/sub] = { kn ; k ∈ N }
(1) find the union of all the sets A[sub]n[/sub] from n = 1 to infinity
(2) find the intersection of all the sets A[sub]n[/sub] from n = 1 to infinity
1 is easy. Any element of A[sub]m[/sub] is also an element of A[sub]1[/sub]. So the union is just the natural numbers.
2, i don't know what to say. Given any finite upper limit M, we can find the intersection as
{0, u, 2u, 3u, ... } with u = lcm(1,2,3, 4, ... , M) but if we let M equal infinity, I don't know if u makes any sense.
![]()
#81 Re: Help Me ! » need a geometry reminder » 2008-09-09 07:07:03
does no one remember any sort of proportionality relation for this? I could have sworn there was one.
#82 Re: Help Me ! » program that solves stuff step-by-step » 2008-09-07 23:32:32
Typically, students want those programs not to learn, but to get the answer on a homework. When it comes time for an exam or quiz, they fail miserably.
hahaha, there are two guys i can think of at my school that only passed math 171 and 271 (calc II and III) because they had a fancy calculator. I said it looks like the number associated with the course (171, 271) corresponds to the cost (in dollars) of the calculator they need to pass the course. ![]()
So I guess it does enable you to pass in some exams or quizzes, but... definitely you're setting yourself up for failure in the very near future. (probably in the next subsequent course)
#83 Re: Help Me ! » program that solves stuff step-by-step » 2008-09-07 12:17:45
man, i love compiling time..
#84 Help Me ! » need a geometry reminder » 2008-09-07 12:11:08
- mikau
- Replies: 9
if we are given the triangle in the attached diagram, and we know the ration of a/b, does that tell give us any equations relating L1, L2, and L3?
#85 Help Me ! » interesting set proble, is this the simplest solution? » 2008-09-05 18:16:55
- mikau
- Replies: 2
The set S is formed according to the following rules:
1: 2 ∈ S;
2: n ∈ S ⇒ n+5 ∈ S
3: n ∈ S ⇒ 3n ∈ S
Find the largest integer in the set:
{1, 2, ... , 2008} that does not belong to S.
My solution:
observation 1: every element of S is of the form 2*3^n + 5m where m and n are natural numbers.
proof by induction: clearly it holds for 2, as 2 = 2*3^0 + 5(0). Suppose by induction that it holds for the first k elements, that is each of those elements is of the form 2*3^n + 5m. then any new element obtained by rules (2) and (3) gives
2*3^n + 5(m+1) and
2*3^(n+1) + 5*(3m) respectively, and clearly m+1, n+1, and 3m are natural numbers if n and m are, and the proof is complete.
observation 2:
Each element of the set is therefore of the form, 2*3^n + 5m and so for any element of the set, we may subtract 5 a certain number of times to get a number of the form 2*3^n, (note n may be 0, and we may not need subtract any 5's)
observation 3: any multiple of 5 cannot be an element of this set.
proof: suppose s is a multiple of 5, if s ∈ S, then by observation 2, we may subtract 0 or more 5's until we obtain a term of the form 2*3^n, but subtracting any number of 5's from a multiple of 5, we still get a multiple of 5. But 2*3^n contains no 5 in its prime factorization, and hence cannot be a multiple of 5. A contradiction. Thus any multiple of 5 cannot be in the set.
Therefore, the maximum integer between 0 and 2008 thats not in the set must be 2005 or greater. Now I just show that 2006, 2007 and 2008 are in the set:
2006: multiply 2 by 3, and add 5 four hundred times
2007, add 5 to 2 four hundred one times
2008, multiply 2 by 3, by 3 again, add 5 three hundred ninety eight times.
so it must be 2005.
was that a good way to go about solving this problem? or is there a more intuitive solution? My solution seems a bit convoluted, and i feel like there must be a simpler argument. ![]()
#86 Re: Dark Discussions at Cafe Infinity » Where to learn higher calculus? » 2008-08-21 12:21:23
Okay, but does that mean vectors in R^n/ C^n, or does it deal with the elements of any vector space?
Seems to me you should be able to develop a calculus for any vector space over a Field that contains an infinite number of elements between a and b...
#87 Re: Dark Discussions at Cafe Infinity » Where to learn higher calculus? » 2008-08-21 06:17:17
I thought Vector Calculus WAS multivariable calculus!
Whats the difference?
#88 Re: This is Cool » 0.9999....(recurring) = 1? » 2008-08-12 13:52:15
if you have 1/3=0.333... & you multiply both sides by 3 then you would get 1=0.999... But then doesn't that make it true that 1 is not equal to 0.999... ?
um.. no? Multiplying both dies of 1/3=0.333 gives you 1 = 0.999..." which says they are equal. It does not say they are unequal. So how would that suggest they are unequal?
#89 Dark Discussions at Cafe Infinity » file organization in Windows XP » 2008-08-04 08:06:44
- mikau
- Replies: 10
So I recently discovered that my hard drive is actually pretty close to full! ![]() Its a 40gb hard drive and I'm up to about 37gb. And I honestly don't know where all that went!
Its a 40gb hard drive and I'm up to about 37gb. And I honestly don't know where all that went!
So I thought I'd find out. I went to the root directory C:\ to view all the folders there, and checked the size of each folder. The three largest folders were:
program files: 16.8 gb
documents and settings: 8.85 gb
WINDOWS: 3.84 GB
thats roughly 29 gb there. But the rest of the 33 folders are pretty much all less than 1 mb in size. Seems like there's about 8 gb unaccounted for. Any ideas where this could be?
#90 Re: Help Me ! » Some Questions way Over my Head.... » 2008-07-26 07:43:07
Proof by example works usually to show that something is not true in all cases. For instance, prove that not all quadratic equations have two unique roots. You can prove this by taking the example of x^2 -4x + 4 = 0, 2 is the only (real) root of this equation. Even if this happened to be the only equation without two unique roots, it would still hold that all of them don't have that.
As for backwards proofs, you have to be careful with which way the implication works in your logic. All dogs have 4 legs but not everything with 4 legs is a dog. In this problem you are given a premise, equation 1 and have to show that equation 1 implies equation 2, so 1 ⇒ 2 (1 implies 2) but you can't just start with 2 and show that 2 ⇒ 1.
What you can do is proof by contrapositive. In which you say suppose 2 is not true, if you can prove that 2 is false implies 1 is false, then clearly if 1 is true, then 2 must be true.
Not however, that many times when showing two equations are equivalent, you can work in both directions, but not always. You must be careful.
#91 Re: Help Me ! » If a trig equation has one answer, how many answers will it have? » 2008-07-25 21:05:57
I'm guessing he means,
if sin(x) = a,
how many angles can satisfy the equation?
in which case the 'answers', or better, the set of values that satisfy this equation are ... an infinite number of values!
However, if you consider them as angles, and consider angles that differ by integer multiples of 360 degrees to be equivalent, then you fill find that for any angle A, you can find another B such that sin(A) = sin(B), in other words, there are two answers. The same holds for cosines.
remember its best to think of sine and cosine functions with the unit circle. The sine of an angle θ is the y coordinate you obtain from rotating the point (1,0) about the origin (counter clockwise) by θ degrees. (or radians). The cosine of θ is the x coordinate of that same point.
So you know if two angles have the same sine if they have the same vertical height on the unit circle, and the same cosine if they have the same horizontal position on the unit circle. See diagram.
But I'm only guessing at what you meant! >.< I just felt like babbling about the unit circle, because I love the unit circle! ![]() Seems to me that if you understand the unit circle, you understand trigonometry!
Seems to me that if you understand the unit circle, you understand trigonometry!
#92 Re: Help Me ! » matrices » 2008-07-25 19:34:45
thanks jane, but didn't I tell you not to prove it? ![]()
fortunately, I got that much of the proof, but that assumes initially that, given ax = 1, there is some matrix y such that ya = 1 (has a left/right inverse implies has a right/left inverse). If we can show one exists, then we can show by the above proof that they must be equal.
I'm simply trying to prove that, if Ax = 1 implies xA = 1.
for one, I noted Ax = 1 implies (Ax)A = A(xA) = A, but I'm not sure if AM = A implies M = I, and so the problem reduced to trying to prove that.
#93 Help Me ! » matrices » 2008-07-24 16:46:59
- mikau
- Replies: 3
reviewing some linear algebra.
Is it true that for an invertible nxn matrix A, that
that is, if A has an inverse, does the inverse works from either side? Don't tell me how to prove it, i just want to know if its true.
#94 Re: This is Cool » Zero !!! » 2008-07-21 05:43:36
hahaha, I even caught my calc teacher at school making that exact mistake, marked it wrong when I said
wrote infinity in red ink. A lot of people thanked me when I pointed out that 'does not exist' was indeed the correct answer.
The two sided rule is just a technicality thats easy to forget. Just an honest mistake, not bs. Did you get enough sleep, Jane? ![]()
#95 Re: This is Cool » Zero !!! » 2008-07-20 15:15:37
because division by exactly zero is undefined. The operation has no meaning. And I think I can hear Ricky groaning when you say 1/∞ is equal to 0.
#96 Re: This is Cool » end of world » 2008-07-19 06:56:31
this post made me laugh.
Does you BRAIN end with that...
hahahaha, that guy is one of a kind!
#97 Re: Dark Discussions at Cafe Infinity » Fake Science ramphant in commercials » 2008-07-04 07:38:56
Hey, thanks, Ricky. It feels better that we've not been using some totally bogus product all this time.
#98 Re: Coder's Corner » installing C++ libraries » 2008-07-01 09:52:44
Thanks for the response!
Yes, I've noticed makefile's typically appear. I opened the readme of a particular library and it gives instructions for Unix installation, and says the process can be emulated for mac or windows. Not sure what that means, though.
In any case, configure, make, and make install. Can you tell me where I can learn how to perform these three steps?
I really know very little about command line processing, which I think is what this is.
#99 Re: Coder's Corner » installing C++ libraries » 2008-06-28 20:36:14
Is it not possible to, for instance, copy the folder of a new library into your particular projects folder, and compile and access the library exclusively in that project?
#100 Re: Dark Discussions at Cafe Infinity » Fake Science ramphant in commercials » 2008-06-28 13:56:08
While we're on the subject of science and oral health, has anyone else heard the claim that Fluoride, an ingredient commonly used in toothpaste that is supposed to strengthen your teeth, actually does no such thing? Many conspiracy theorists seem to endorse this notion, and I've often wondered if there's any truth to it.