Math Is Fun Forum

  Discussion about math, puzzles, games and fun.   Useful symbols: ÷ × ½ √ ∞ ≠ ≤ ≥ ≈ ⇒ ± ∈ Δ θ ∴ ∑ ∫ • π ƒ -¹ ² ³ °

You are not logged in.

Pages: 1 2

#26 Re: Help Me ! » Finally back! Need help on this advanced algebra problem. » 2018-07-02 05:50:45

!nval!d_us3rnam3

Ok, thanks!

#27 Help Me ! » Finally back! Need help on this advanced algebra problem. » 2018-07-02 05:10:44

!nval!d_us3rnam3
Replies: 2

(a) Determine all nonnegative integers $r$ such that it is possible for an infinite arithmetic sequence to contain exactly $r$ terms that are integers. Prove your answer.

(b) Determine all nonnegative integers $r$ such that it is possible for an infinite geometric sequence to contain exactly $r$ terms that are integers. Prove your answer.

I know this problem may have been answered before, but I didn't find those explanatory enough. If you can find a thorough resource, refer me to that, please. Otherwise, solve it here.

#28 Re: Help Me ! » Triangle Proofs » 2017-05-18 13:35:16

!nval!d_us3rnam3

Em, whatever. I've finished it already tongue
Thanks anyway!

#29 Re: Help Me ! » Triangle Proofs » 2017-05-17 01:32:31

!nval!d_us3rnam3

Thank you!
I just need help with one more problem. (Please don't just give me a link to somewhere else, work me through some of it here.)

Two circles are externally tangent at point

, as shown. Segment
is parallel to common external tangent
Prove that the distance between the midpoints of
and
is

EDIT: I extended lines AC and BD to meet at Q, then proved that QAB is similar to QCD. Then what?
And y duz the

insist on creating its own line -.-

#30 Re: Help Me ! » Triangle Proofs » 2017-05-16 13:48:02

!nval!d_us3rnam3

What are the sign differences, may I ask? Just wanna make sure I didn't miss something.

#31 Re: Help Me ! » Triangle Proofs » 2017-05-15 02:09:17

!nval!d_us3rnam3

Yknow, I did it already, but I'll still post my answers for all of them.
(b) x^2=y^2+xy
(c)r^2+r=1, r = {sqrt(5)-1}/2
(d) cos 36 = {sqrt(5)+1}/4, cos 72 = {sqrt(5)-1}/4

#32 Re: Help Me ! » Triangle Proofs » 2017-05-12 08:21:32

!nval!d_us3rnam3

Can you actually walk me through part (d)? I did (a), (b), and (c).

#33 Re: Help Me ! » Triangle Proofs » 2017-05-11 06:08:22

!nval!d_us3rnam3

Can you walk me through parts (b), (c), and (d)? I'm having a little trouble with them. (a) is easy enough, though.
Many thanks!

#34 Re: Help Me ! » Yes, bob bundy, again. XD Need answer by tonight. Thanks! » 2017-04-06 08:24:55

!nval!d_us3rnam3

What did you get as your cone volumes and final answer? Just checking my answers.

#35 Re: Help Me ! » Yes, bob bundy, again. XD Need answer by tonight. Thanks! » 2017-04-06 07:44:44

!nval!d_us3rnam3

Thank you so much! big_smile

#36 Re: Help Me ! » Yes, bob bundy, again. XD Need answer by tonight. Thanks! » 2017-04-06 05:45:30

!nval!d_us3rnam3
bob bundy wrote:

So you end up with

4x = 3y  and

4x + 24 = 10 - 3y

Replacing 4x in the second equation with 3y (since 4x = 3y) and adding 3y to both sides gives 6y + 24 = 10. Subtracting 24 from both sides gives 6y = -14, or y=-7/3. We can't have negative lengths. I think the equation screwed up somewhere. wink

EDIT: Otherwise, your solution is nice and clear, and I feel that I can take the rest.

#37 Re: Help Me ! » Yes, bob bundy, again. XD Need answer by tonight. Thanks! » 2017-04-06 05:26:08

!nval!d_us3rnam3

I get a negative fraction as y. X is equal to y too, for some reason.... what Did you mess up somewhere?

#38 Re: Help Me ! » Yes, bob bundy, again. XD Need answer by tonight. Thanks! » 2017-04-06 03:14:59

!nval!d_us3rnam3

Is there an easier way than that, because I'm still confused? Technically, all we need to do is find the top length of the frustum, then we can find the bottom length of the frustum easily. All that we need after that is to find a formula for the volume of a frustum and prove it. (That doesn't really seem easy, but now I'm desperate. I've visited 6 help sites and I'm still none the wiser. Can you be a little more detailed?) hmm

#39 Re: Help Me ! » Yes, bob bundy, again. XD Need answer by tonight. Thanks! » 2017-04-06 01:29:35

!nval!d_us3rnam3
bob bundy wrote:

hi !nval!d_us3rnam3

http://i.imgur.com/UBcgXOV.gif

If you 'drop' a perpendicular from A to the base you can work out FB using Pythagoras.

Then use similar triangles to work out EF and GH.

Then it should be straight forward to finish the task.

Well, I'll need to find the volume of the top cone. Either that, or I prove a rather confusing frustum volume formula. I know the height is 6, and FB is 8, and slant height is 10, so now what?

#40 Help Me ! » Yes, bob bundy, again. XD Need answer by tonight. Thanks! » 2017-04-05 13:58:05

!nval!d_us3rnam3
Replies: 17

A sphere with radius 3 is inscribed in a conical frustum of slant height 10. (The sphere is tangent to both bases and the side of the frustum.) Find the volume of the frustum.

I haven't tried much, I'm just really stuck, can you give me a solution skeleton (i.e. where I prove a few things myself)? Thanks in advance!
~ !nval!d_us3rnam3

P.S. Please, don't give me another link to somewhere else on the website, because I've probably read it already. Just help me out here. Thanks again smile

P.S.S. If you have time, what's the list of working emojis on this website, other than smile, wink, big_smile, sad, tongue, yikes, and shame? Thanks yet again!

P.S.S.S. How do people get the title of "Real Member"?

#41 Re: Help Me ! » 3d plane in a cube » 2017-03-27 10:08:02

!nval!d_us3rnam3
kk63353 wrote:
bob bundy wrote:

SA = 10/3

From the second pair SA/SD = AQ/RD

=> RD =  1 x (5+10/3)/(10/3) = (15+10)/10 = 25/10 = 2.5

Can't we just say SA/SD=2/5=AQ/RD, so since AQ=1, RD=5/2?

I was thinking the exact same way. Why not use the slope of the line, and the height it gains as it crawls along the edge of the cube, rather than a big long solution that I partially didn't understand? This is my reasoning:

PA = 2, and AQ = 1, so line PQ has a slope of 1/2. Therefore, when the line QR, which is just a continuation of PQ, goes 5 units laterally, it climbs 2.5 units. Therefore, DR = 2.5.

Q.E.D.

#42 Re: Help Me ! » Tough question, need answer before tomorrow night. Thanks! » 2017-03-25 06:00:15

!nval!d_us3rnam3

Power of a point, in this diagram, looks like PA^2 = PD*PB = PC^2. 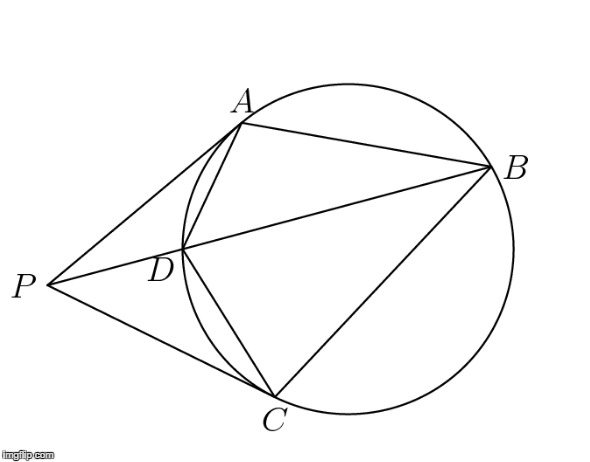1m35i9.jpg

#43 Re: Help Me ! » Tough question, need answer before tomorrow night. Thanks! » 2017-03-25 02:46:01

!nval!d_us3rnam3

I've already proved similar triangles. Just need a little help going from there. Can you help me through the ratios? Most of the time I get the same result as using Power of a Point.

I'll be on this forum fairly actively if I need any homework help.

#44 Help Me ! » Tough question, need answer before tomorrow night. Thanks! » 2017-03-24 16:00:49

!nval!d_us3rnam3
Replies: 5

Let $\overline{PA}$ and $\overline{PC}$ be tangents from $P$ to a circle. Let $B$ and $D$ be points on the circle such that $B$, $D$, and $P$ are collinear. Prove that $AB \cdot CD = BC \cdot DA$.

I've already tried Power of a Point and similar triangles, but I can't seem to get anything to work. Can someone help me directly? By the way, don't post another link from this website, as I've probably checked that one already. Many thanks! smile

P.S. I need the answer before Saturday night.

#45 Re: Help Me ! » Help me; need answer before tonight. Thanks! » 2017-03-18 09:03:01

!nval!d_us3rnam3

Thank you so much for helping! smile

#46 Help Me ! » Help me; need answer before tonight. Thanks! » 2017-03-18 02:52:19

!nval!d_us3rnam3
Replies: 3

Let the incircle of triangle $ABC$ be tangent to sides $\overline{BC}$, $\overline{AC}$, and $\overline{AB}$ at $D$, $E$, and $F$, respectively. Prove that triangle $DEF$ is acute.

I have tried proving that triangle DEF's angles were less than the opposite angles in triangle ABC, but that wasn't really complete. Can anyone help? Thanks! big_smile

Pages: 1 2

Board footer

Powered by FluxBB