Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2007-03-06 11:51:38
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Hi! Are you ready for a G A M E ? Go to Post #12 (see #s right) and have fun!![]() !
!
____________________________________________________
Here is a little preview:
This was discovered by 5 year old boy who later was called Mozart of mathematics.
What's his name?

Last edited by skymus (2010-06-04 05:13:41)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#2 2007-03-06 12:05:12
- Zhylliolom
- Real Member

- Registered: 2005-09-05
- Posts: 412
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Sounds good Kyle, I'm surprised you know of Tao. But honestly, I've heard Euler, Gauss, Erdos, and others referred to as "the Mozart of mathematics", and this "discovery" isn't something so unique that only one child would figure out, I'm sure at least one of these others realized such a thing when they were quite young.
Offline
#3 2007-03-06 20:53:08
- Toast
- Real Member

- Registered: 2006-10-08
- Posts: 1,321
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Funny thing is, even though he's Aussie, and the 'Mozart of Mathematics', go up to any average person on the street and 9/10 times they won't have a clue who he is.
Offline
#4 2007-03-07 06:04:12
- Zhylliolom
- Real Member

- Registered: 2005-09-05
- Posts: 412
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
I would bet even as much as 9/10 math majors wouldn't know who he is, unless they are particularly interested in mathematics competitions (that is how I first learned of him). But who knows, I've never asked anyone if they know of him before.
Offline
#5 2007-03-07 06:05:23
- lightning
- Real Member
- Registered: 2007-02-26
- Posts: 2,060
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
i don't know him
Zappzter - New IM app! Unsure of which room to join? "ZNU" is made to help new users. c:
Offline
#6 2007-03-09 10:35:46
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
![]() - good discussion!
- good discussion!
Simple discovery is most often a deceptive one. It usually contains a surprise element. The magic is not in what it contains, but rather in what it doesnt. ![]()
1 + 3 + 5 = 3*3 what principle does it contain and what it does not?
If 1 + 3 + 5 = 3^2, does 2 + 4 + 6 = 4^2 ?... Obviously not.
Find the play (rule/formula) for multiples a and b, which would work for both:
for
and for .
When you find the a * b rule, then determine if the same rule plays out for
natural, whole, integers, rational, irrational numbers X1, X2,
in equation . Give some examples.

Now come back to 1 + 3 + 5 = 3*3 and see the hidden simplicity in it.
Mozart music also contains the highest level of deceptive simplicity,
which Albert Einstein recognized and adored in his violin journey.
Last edited by skymus (2010-06-04 05:01:51)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#7 2007-03-12 09:16:59
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
... breaking down the puzzle ![]() :
:

if ,
so we have that X1 + X2 + ... + Xn = a * b for a = n and b = (X1 + Xn)/2:
Now it is your turn:
2 + 4 + 6 = _ * [( _ + __ ) / 2] = _ * _ ?
Next, may you bring an example with integers? ![]()
The Lady Tasting Tea. How Statistics Revolutionized Science in the XXth Century by David Salsburg. The book author described discovery of the five-year-old in a few sentences (p.138, Chapter 14. THE MOZART OF MATHEMATICS). It does deserve our playfull minds... let's have fun and may even create a game on the numbers right here.
Last edited by skymus (2010-06-04 05:31:12)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#8 2007-03-12 09:18:52
- lightning
- Real Member
- Registered: 2007-02-26
- Posts: 2,060
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
i thought mozart was a composer
Zappzter - New IM app! Unsure of which room to join? "ZNU" is made to help new users. c:
Offline
#9 2007-03-12 09:41:05
- Devantè
- Real Member
- Registered: 2006-07-14
- Posts: 6,400
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Right. So what do you think the 'Mozart of Mathematics' means?
Offline
#10 2007-03-13 03:45:13
- skymus
- Member
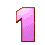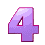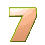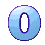
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Here is an example with rational numbers:
-10.9 - 9.8 - 8.7 - 7.6 = 4 * [(-10.9 + -7.6) / 2] = 4 * [(-18.5) / 2] = 4 * (-9.25) = -37
May you bring your example with rational numbers? ![]()
Now come back to our original puzzle!

Pascal Triangle
Last edited by skymus (2010-06-04 07:01:30)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#11 2007-03-21 04:14:56
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Let's now play a little game: !![]() !
!
Come back to our original formula:
1 + 3 + 5 = 3*3
How many numbers are on the left side of the above equality? That's right: 3 !
Follow the same reasoning for other numbers as it is done below:
Example: roll a 6-sided dice to receive amount of number participants in the game:
e.g., Roll #1 = 5 and you make equality of 5 members. Always start from 1 and add 2 to get next number:
1 + 3 + 5 + 7 + 9 = 5*5
next: Roll #2 = 2, then 1 + 3 = 2*2
Roll #3 = 6, then 1 + 3 + 5 + 7 + 9 + 11 = 6*6
Roll #4 = 4, then 1 + 3 + 5 + 7 = 4*4
Roll #5 = 1, then 1 = 1*1
Game: roll 5 times and count the sum of all 5 rolls. The highest sum wins. ![]()
Let's count our 5 rolls: 25 + 4 + 36 + 16 + 1 = 82.
Roll your dice 5 times and try to reach that 82.
Your turn...give me your Roll #1 = ___ ![]()
Last edited by skymus (2007-03-22 09:29:31)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#12 2007-04-02 04:59:12
- skymus
- Member
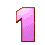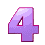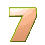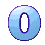
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
![]()
![]() gives... 6
gives... 6
for Roll # = 6, write down the equality here:
1 + ... = 6 * 6
![]()
Last edited by skymus (2007-04-02 05:04:58)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#13 2007-04-02 05:23:19
- lightning
- Real Member
- Registered: 2007-02-26
- Posts: 2,060
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
1+5=6 there you got all figured out and it only took me............................1 hour nah i'm joking it actully took me 0.01 secs to figure that out! lol
Zappzter - New IM app! Unsure of which room to join? "ZNU" is made to help new users. c:
Offline
#14 2007-04-02 05:31:38
- Devantè
- Real Member
- Registered: 2006-07-14
- Posts: 6,400
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
He said write an equality, and plus it would be wrong if that wasn't even asked, anyway. It isn't basic mathematics, you'll get taught about equalities and inequalities in later years.
Offline
#15 2007-04-02 05:35:47
- lightning
- Real Member
- Registered: 2007-02-26
- Posts: 2,060
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
i'm in year 7 not the high school but a couple of days soon and i will be in 1st year whooooo hoooooo!!!!!!!!!!!
Zappzter - New IM app! Unsure of which room to join? "ZNU" is made to help new users. c:
Offline
#16 2007-04-26 10:08:05
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
For previous case of Roll # = 6, the equality is:
1 + 3 + 5 + 7 + 9 + 11 = 6 * 6
Next, let us say ![]() gives... Roll # = 3:
gives... Roll # = 3:
for Roll # = 3, write down the equality here:
1 + ... = 3 * 3
_______________________________________
![]()
![]()
![]()
Now let us have even more fun!
Let's say that ![]() gives...
gives...
1
... Roll # = (∫x³dx)-¹
0
First, count Roll# = __
Then, write down the equality here: _ + _ + ... = _ * _
Have fun ![]()
Last edited by skymus (2007-04-26 10:16:48)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#17 2007-05-16 07:46:20
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
![]()
![]()
![]()
For Roll # = 3 the equality is: 1 + 3 + 5 = 3 * 3.
![]()
![]()
![]()
________________________________________________
![]()
![]()
![]()
![]()
![]()
Use the table to find ![]() :
:
1
Roll # = (∫x³dx)-¹
0
![]() Anybody give it a try?..
Anybody give it a try?.. ![]()
Last edited by skymus (2007-05-17 11:31:58)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#18 2007-06-09 11:42:17
- skymus
- Member
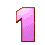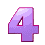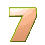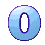
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
![]()
![]()
![]()
ok, ok. Let's do it together!
![]()
![]()
![]()
![]()
![]()
Find:
1
Roll # = (∫x³dx)-¹
0
![]()
Use the table to find it:
1
for (∫x³dx)-¹: (x^4/4)-¹ = 4/x^4 ??? Nope! See Mr. Franklin's corrective post below
0
It is:
1
for (∫x³dx)-¹ we plug 0 and 1 into formula as follows:
0
(x^4/4)-¹ ol¹ = [(1^4)/4 - (0^4/4)]-¹ = (1/4 - 0/4)-¹ = (1/4)-¹ = 4
![]()
![]()
![]()
![]()
![]()
Therefore:
1
(∫x³dx)-¹ = 4 and thus Roll # = 4
0
![]()
![]()
![]()
PS I've got too much pre-occupied with placing correct math symbols as x^4 and ∫
to miss on the flow of the calculation itself.
It is interesting that we have x³ ready to use here, which is x^3, but not the same for x^4.
Thank you, John, for interaction.
Last edited by skymus (2010-06-01 05:42:53)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#19 2007-06-11 06:56:40
- John E. Franklin
- Member

- Registered: 2005-08-29
- Posts: 3,588
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Right, the integral from 0 to 1 is (1^4)/4 - (0^4)/4, which is 1/4 - 0/4, which is 1/4.
Then you flip 1/4 over to 4/1.
igloo myrtilles fourmis
Offline
#20 2007-07-25 04:04:11
- skymus
- Member
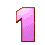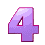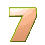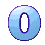
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
![]()
![]()
![]()
![]()
![]()
For previous case of Roll # = 4, the equality is:
1 + 3 + 5 + 7 = 4 * 4
![]() Do you remember?
Do you remember? ![]()
1
(∫x³dx)-¹ = 4 and thus Roll # = 4?
0
______________________________________
Ok, now is your turn. ![]()
May you roll a dice to give me your Roll #?
![]()
![]()
![]()
Last edited by skymus (2007-07-25 04:25:17)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#21 2007-10-02 12:51:24
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
So, Post #12 defined the game out of 5 rolls.
The number to reach and overcome is = 82.
Until this moment ![]() gave us the following rolls:
gave us the following rolls:
6: 1 + 3 + 5 + 7 + 9 + 11 = 6 * 6 in Post #13
3: 1 + 3 + 5 = 3 * 3 in Post #18
4: 1 + 3 + 5 + 7 = 4 * 4 in Post #19
We need two more rolls!
![]()
![]()
![]()
![]()
![]() CAN anybody ROLL the DICE?.... ANYBODY ? . . . .
CAN anybody ROLL the DICE?.... ANYBODY ? . . . . ![]()
![]()
![]()
![]()
![]()
Let's do the deal: you will roll the dice and I will count the numbers!
Last edited by skymus (2007-10-04 06:47:06)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#22 2007-11-23 13:23:41
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
![]()
![]()
![]()
Winnie the Pooh: Hellooooooo.... Is anybody at home??????
![]()
![]()
Rabbit: No, NOBODY!
...
![]()
Winnie (to himself): if somebody says NOBODY, than it means there should be somebody.
_______________________________________________________________
Winnie:
Can Anybody Roll the Dice?
![]()
![]()
![]()
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#23 2007-11-23 14:50:28
- Identity
- Member

- Registered: 2007-04-18
- Posts: 934
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Winnie is philosophical thinker
Offline
#24 2008-01-28 09:29:02
- skymus
- Member
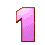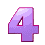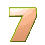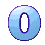
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
![]()
So, Post #12 defined the game out of 5 rolls.
The number to reach and overcome is Total = 82.
Until this moment ![]() gave us the following rolls:
gave us the following rolls:
Roll #1 = 6: 1 + 3 + 5 + 7 + 9 + 11 = 6 * 6 in Post #13
Roll #2 = 3: 1 + 3 + 5 = 3 * 3 in Post #18
Roll #3 = 4: 1 + 3 + 5 + 7 = 4 * 4 in Post #19
Total = 36 + 9 + 16 = 61
We need two more rolls!
Today we will Roll #4 = ...
Ready, Set and Ready, Go: . . . 5
Thank you, ![]() !
!
Thus, Roll #4 = 5: 1 + 3 + 5 + 7 + 9 = 5 * 5
Total: 61 + 25 = 86
![]()
![]()
![]()
![]()
![]()
Can Anybody roll the dice for the last Roll #5? ![]()
Last edited by skymus (2010-06-04 04:53:01)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
#25 2010-06-01 06:29:17
- skymus
- Member
- Registered: 2007-03-06
- Posts: 16
Re: 1+3=2^2, 1+3+5=3^2, 1+3+5+7=4^2 etc.
Do you remember...
1
Roll # = (∫x³dx)-¹ = ?
0
![]() We still need one more roll ... Anybody wants to give it a try?..
We still need one more roll ... Anybody wants to give it a try?.. ![]()
P.S. You may use the table to find ![]() :
:
1
(∫x³dx)-¹ = ?
0
Last edited by skymus (2010-06-01 09:25:02)
Playful Math: Even Double
Aim to Win-Win
ArtuM101Options
Offline
Pages: 1