Math Is Fun Forum

Ok, what we want to do basicly in a 3d engine is convert 3d, to 2d. We are creating an illusion to graph 3d objects on a 2d plane (a computer or tv screen) so that they appear to be three dimensional even though its being displayed on a flat surface.

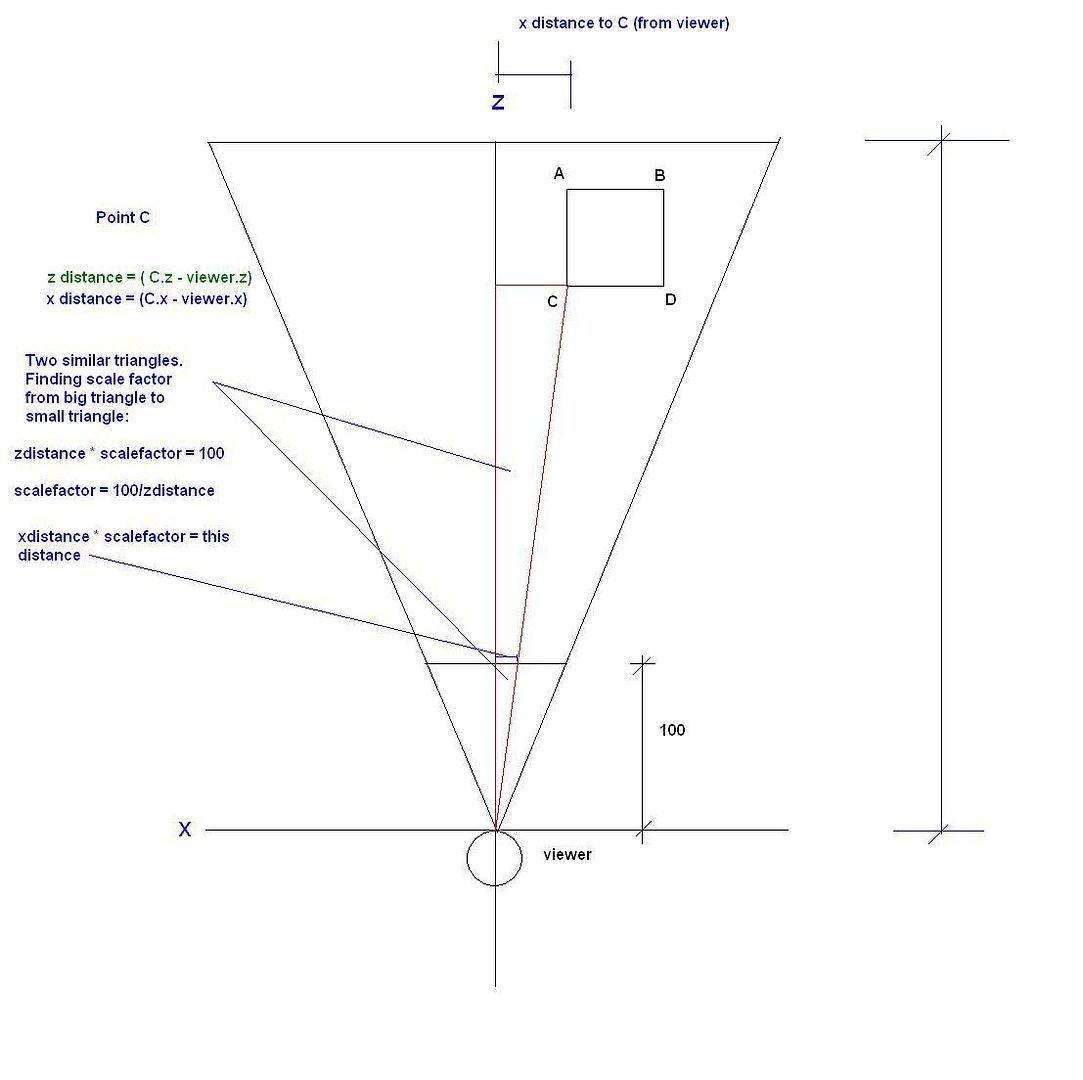
A computer screen is supposed to be like a window to a world. If you were to look through a window at a box, the image of the box would be passing through the window at a certain point and entering your eyes. If you were to replace the window with a board and draw the box at the exact same place where the original box passed through the glass, it would look just like the real box through the window.

The first pic below illustrates this. If your standing behind a window, looking at a box. And you look at corner C, you are looking through a specific point on the glass. The point where the redline I drew, thats drawn from your eyes to the box, crosses through the window. If you were to draw corner C at that point on the window, and draw all the corners where they intersect the glass, and connect the points with lines. You would see a 3d image of the box exactly as you saw it through the glass.

A computer screen is just like a window to another world so we can do the same to graph 3d points, only it must be done mathematically. First I placed the viewer on an X,Z plane at 0,0. And placed a 2 by 2 box 10 units in front of the viewer. I then placed a small "screen" in front of the viewer. We want to know exactly where every point intersects that screen to graph it.

First we draw a line from the viewer to a point (we'll use point C) Then a line from the viewers location, straight forward, and finally, a line that passes through point C that is paralell to the computer screen or window. We know have two similar triangles. On the big triangle, the horizontal piece is the horizontal distance from the viewer to the point. On the small triangle, this corresponding side is the distance from the center of the computer screen to the point where point C will be placed. Since the triangles are similar all we have to do is scale the parts. We will make the vertical length of the small triangle 100 units. (100 will most likely be bigger number even though its drawn smaller but it still works). We then have to find the scale factor of the big triangle to the small triagnle. First we find the Z distance to the object by subtracting the viewers Z coordinate from the objects Z coordinate. The distance in this case will be 10 since I set the point 10 units out. So now we have corresponding side lengths so we can find the scale factor. 100 * scalefactor = 10. scalefactor = 0.1. We can now use this scale factor to find the horizontal side of the small triangle. We find the x distance from viewer to object by subtracting the viewers x from the objects x. We then multiply by the scale factor to get the length of the small triangle and the location on the computer screen.

This only gave us the new x coordinates. You also need to do the same thing on the Y,Z plane to find the new height as well, but its the same process so I don't think we need to go through it. 

The first pic below is an illustration of what we're doing.

The bottom pic shows using the system with the x,y,z coordinates of a 2 by 2 box 10 units away, translated and graphed using this system. (except I scaled the distances in relation to 200 instead of 100 to make it easier to graph.

results:

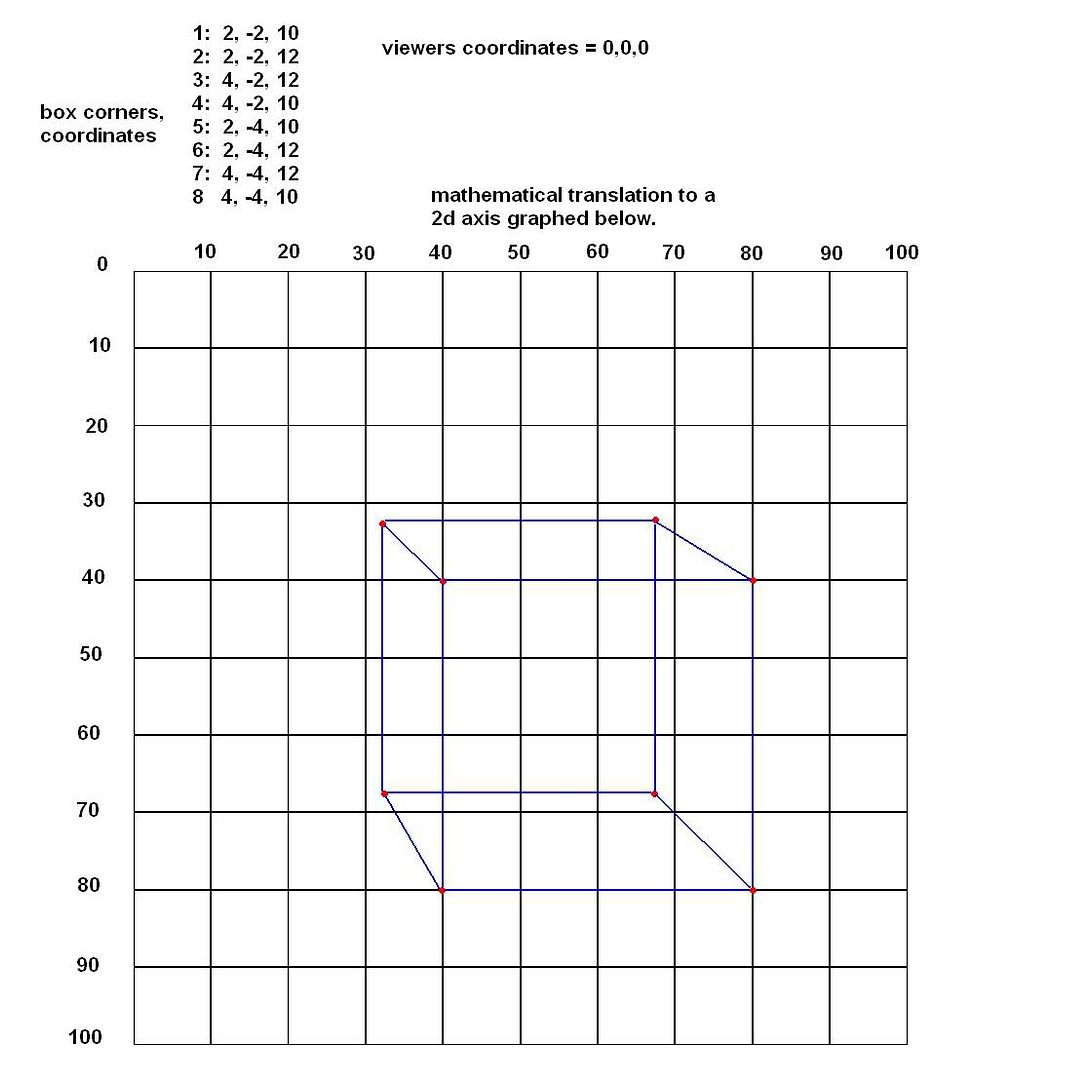
First we find the perpendicular distance to the object from the viewer, by finding the z distance between them. We subtract the objects

Things are going well. I just ignored the slight inaccuracies. I already tried writing pi to a lot more decimal places but that just ended up writing really small numbers in scientific notation when it should have been zero.

But in the end, it seemed the inaccuaracies were small enough not to be detrimental to the program.

It would be much easier (and clearer) to just pass in points as arguements, rather then having to individually pass in horizontal and vertical coordinates. But then I'd have to define a new function for every plane. xy, xz, yz. I wonder if it would be worth it...

Well I guess I could just take the sine of the complement angle since thats what cosine means and the sine function appears to be working fine. (I call this sort of thing "humoring the computer")

Great minds think alike. But I have my reasons. I already have a class "point" with x,y,z member data. But this polar angle function is going to be used not just on the x,y plane. Its going to be used on x,z plane, a y,z plane, as well as the x,y plane. So if I use x and y, in somecases I'd have to use y, for x, instead of y, for y. The same reason why I didn't pass in "points" as arguements. Because sometimes I'll be using only their y,z coordinates, other times their x,z coordinates, etc. There is probably a simple way to do it with points but I haven't thought of one yet.

I'm writing a math program to calculate the location of a point (on an x,y plane) based on its x,y, z coordinates, the observers x,y,z coordinates, and the angle at which he's looking. Basicly I'm reinventing the 3d engine myself, trying to figure things out on my own. I've heard real 3d engines just use matrices but my system seems to work anyways.

Your object and origin suggestions are good, the only reason I didn't pic "origin" is because that usually means 0,0,0.

I really need to rename the parameters... :-/

Hey it works! Thanks again mathisfun! Are there functions for arcsin, arccos, and arctan?

Thats exactly what I'm looking for! :-D Thanks a yotta, Mathisfun!

??? e as in the natural logarithm?

Thanks, man. :-)