Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#126 Re: Help Me ! » Math Review » 2013-09-11 02:22:11
If there is a goat tied to a rectangular barn on a 50 foot lead and the barn is 20 feet by 20 feet (floor), what is the maximum grazing area? If there are regions you can't find the area of, provide as good an estimate as you can. Assume the goat is tied to a corner outside the barn, cannot get in, and that the barn is not grazing area. (Remember, this will be based on parts of circles, no other shapes...the goat's rope will only get shorter when he tries to go around the barn...)
6. How much of the 50 foot circle can the goat reach without getting interrupted by the barn? What is that area?
Answer: I would say it can go 3/4 of the area. So 3/4 x 50^2 x pi = 1875 PI
7. When the rope goes around the barn, what is the new radius? How much of a circle can it make without hitting the barn or overlapping area you've already found? What is that area?
Answer: The area for this would be 1/4 and 30 would be the new radius here. So 1/4 x 30^2 x PI = 225 PI
8. When the rope goes around the barn the other way, what is the new radius? How much of a circle can it make without hitting the barn or overlapping area
you've already found? What is that area?
Answer: This would be the same as #7, answer being 225 PI.
9. The areas you found in 7 and 8 overlap each other. How much do they overlap? What *approximate* shape do they make? What is that area?***
10. What is the total grazing area the goat can reach?***
#127 Help Me ! » Math Review » 2013-09-11 01:32:21
- demha
- Replies: 42
I got a math review today. I just wanted help to to check if I got these right and/or help understand any questions that I need to know better. Any questions/answers with this symbol ( *** ) means that I need help on it or do not understand. Thank you!
I have a pizza. The radius is 10 inches long. The pizza was cut into 16 equal slices. When 1 slice was left, my sister and I both wanted it, so we agreed to cut it in half, but I like the crust more than she does, so we decided to cut it the "other way." In other words, the two pieces would not be symmetrical. The inside piece would contain all topping, and the outer piece would contain some topping and some crust.
1. Find the area of the whole pizza.
Answer: (pi)(10^2) = 314.159
2. What is the area of one piece of pizza?
Answer: 314.159 divided by 16 = 19.634
3. What is the area of a half-piece?
Answer: 19.634 divided by 2 = 9.817
4. What would the area of the whole pizza be if it were made of half pieces?***
Answer: I am guessing they mean the 9.817 pieces. So 16 whole pieces make a pizza. They want to know how many halfs so 16 x 2 = 32. Now I do 32 x 9.817 = 314.144. Is this method correct? If not, what is the correct way?
5. What is the radius of a half-piece? (ie, where do I need to cut to make two equal halves out of a piece?)***
Answer: The area of half a piece is 9.817. So I do 9.817 divided by pie which comes up to 3.124, then i square it to get 1.767. Is this correct?
---
NOTE: this is the first half. i am currently doing the second half and will post later for help on this topic.
#128 Re: Help Me ! » Circumference and Arc Length » 2013-09-03 04:24:36
Ah, thank you once again Mr. Bob for spending your time to check these for me ![]()
Sent in the lesson and got 10.000.
#129 Re: Help Me ! » Circumference and Arc Length » 2013-09-03 02:14:41
I have some more from my next lesson. I would like to know if I got them right.
Area of Circles and Sectors
~What is the area of the circle if the radius is: ~
1. 4 - i said C
A 23*pi
B 18*pi
C 16*pi
D 34*pi
E 41*pi
F 60*pi
2. SQRT(3) - i said B
A 9*pi
B 3*pi
C 1*pi
D 5*pi
E 6*pi
F 7*pi
3. 7 - i said E
A 67*pi
B 53*pi
C 75*pi
D 82*pi
E 49*pi
F 34*pi
4. 6x - i said D
A 29 x^2 * pi
B 84 x^2 * pi
C 65 x^2 * pi
D 36 x^2 * pi
E 15 x^2 * pi
F 75 x^2 * pi
5. 10 - i said A
A 100*pi
B 89*pi
C 54*pi
D 72*pi
E 37*pi
F 55*pi
~What is the radius if the area of the circle is: ~
6. 9(PI) - i said F
A 7
B 2
C 5
D 6
E 4
F 3
7. 4x^2(PI) - i said B
A 5x
B 2x
C 9x
D 3x
E 6x
F 1x
8. 25(PI) - i said A
A 5
B 7
C 9
D 15
E 8
F 4
9. 81(PI) - i said A
A 9
B 3
C 5
D 7
E 2
F 6
10. 5(PI) - i said D
A sqrt 7
B sqrt 3
C sqrt 8
D sqrt 5
E sqrt 4
F sqrt 9
11. (9/16)PI - i said E
A 7/6
B 3/1
C 5/2
D 9/5
E 3/4
F 4/1
12. 25y^2(PI) - i said D
A 9y
B 3y
C 6y
D 5y
E 2y
F 10y
13. 16z^2(PI) - i said C
A 9z
B6z
C4z
D7z
E 5z
F 2z
14. t^2(PI) - i said D
A 3.146
B 5
C 2
D t
E 9
F 7
15. (PI) - i said E
A 2
B 6
C 8
D 3
E 1
F 5
~What is the area of the sector if the radius is 6 and the degree measure is: ~
16. 26 - i said C
A 1.9*pi = 9.523
B 6.7*pi = 3.491
C 2.6*pi = 8.168
D 5.1*pi = 7.054
E 9.2*pi = 3.115
F 7.8*pi = 1.274
17. 30 - i said F
A 6*pi
B 5*pi
C 9*pi
D 1*pi
E 6*pi
F 3*pi
18. 50 - i said A
A 5*pi
B 4*pi
C 3*pi
D 9*pi
E 2*pi
F 7*pi
19. 90 - i said D
A 8*pi
B 3*pi
C 1*pi
D 9*pi
E 7*pi
F 2*pi
20. 120 - i said F
A 23*pi
B 74*pi
C 89*pi
D 24*pi
E 59*pi
F 12*pi
#130 Re: Help Me ! » Circumference and Arc Length » 2013-09-03 01:32:14
This is what I got and the teacher said they were all correct. Thank you for your help ![]()
1. c correct
2. f correct
3. a correct
4. d correct
5. f correct
#131 Help Me ! » Circumference and Arc Length » 2013-08-28 04:42:03
- demha
- Replies: 5
I'm not understanding as to how to solve these. I would really appreciate a good explanation as to how to solve them. Maybe you could create a problem similar to one below and solve it step-by-step explaining what to do (I would REALLY love that ![]() ).
).
What is the radius if:
1. n=30 L=1/3xy(pi)
A 6xy
B8xy
C2xy
D10xy
E 3xy
F 14xy
2. n=40 L=8/9(t)(pi)
A 20t
B5t
C9t
D18t
E 12t
F 4t
3. n=15 L=(21/36)pi
A 7
B21
C28
D62
E 56
F 14
4. n=5 L=1/2pi
A 24
B30
C45
D18
E 66
F 39
5. n=18 L=6(y)pi
A 30y
B45y
C120y
D90y
E 15y
F 60y
#132 Re: Help Me ! » Review » 2013-08-14 04:07:28
Would this method be correct?
cos(30)=x/10
10 cos(30) = x
cos(30) = 1/2
so10 *1/2 = 5
#133 Re: Help Me ! » Review » 2013-08-14 03:58:21
Hi Bob,
My teacher said everything is correct, but for number 1 she wants me to use trigonometry to solve it. Here is the question again with my original answer:
1.
Q. A 30-60-90 triangle has a hypotenuse of 10. Use trig to find the short side. Show your work.
A. Answer is 5. Shortest side is always half of the hypotenuse. The longest side would be the shortest leg and (sqrt3).
---
What equation (or method) am I supposed to use exactly?
#134 Re: Help Me ! » Review » 2013-08-12 14:07:47
So do I do this:
cos(60) = g/12
.5 = g/12
g = 12 x .5
g = 6
So the ladder is 6 feet away from the wall, then we do:
6 - 3 = 3.
The base of the ladder from the bottom of the fence is 3 ft.
Is this method correct?
#135 Re: Help Me ! » Review » 2013-08-12 07:13:23
image
#136 Re: Help Me ! » Review » 2013-08-12 07:09:25
#3.
b = c^2 - a^2?
b = 16^2 - 8^2
b = 256 - 64
b = 192
(after squaring)
13.856 = b
I DID IT!!
---
#8.
I uploaded an image of my diagram. Not too sure if its correct though. And what kind of equation would I be making?
#137 Help Me ! » Review » 2013-08-12 04:02:26
- demha
- Replies: 9
This is a review I need to do. It will involve Triangles, Sohcahtoa, Pythagorean Theorem and the Special Right Triangles (30 - 60 - 90 and 45 - 45 - 90). Please help me understand them and check if they are correct: (NOTE FOR #3 and #4, there must be something wrong. I thing I am doing something wrong in #3. Help would be appreciated! I would like to learn a method to find the answer if mine is wrong.)
1.
Q. A 30-60-90 triangle has a hypotenuse of 10. Use trig to find the short side. Show your work.
A. Answer is 5. Shortest side is always half of the hypotenuse. The longest side would be the shortest leg and (sqrt3).
2.
Q. A 30-60-90 triangle has a hypotenuse of 10. Use special right triangle formulas to find the long side. Show your work.
A. We understand that the shortest leg is 5.
The shortest leg is 5.
The hypotenuse is (5 x 2) or 10.
The longest leg will be 5 (sqrt3)
The final answer for the longest leg will be 8.660
3.
Q. A 30-60-90 triangle has a hypotenuse of 16 and a short side of 8. Use the Pythagorean theorem to find the third side. Show your work.
A.
a^2 + b^2 = c^2
8^2 + 16^2 = c^2
64 + 256 = c^2
320 = c^2
(after squaring)
C = 17.888
4.
Q. A 30-60-90 triangle has a hypotenuse of 16 and a short side of 8. Use special right angle formulas to find the third side. Show your work. Does your answer match what you got on number 3?
A.
8 (sqrt3) = 13.856
5.
Q. A 45-45-90 triangle has a leg of 4[sqrt(2)]. What is the hypotenuse? Show your work.
A.
4 (sqrt2) x (sqrt2) = 4 (sqrt4) = 8
6.
Q. A right triangle has legs of 4 and 5. What is the hypotenuse? Show your work.
A.
a^2 + b^2 = c^2
4^2 + 5^2 = c^2
16 + 25 = c^2
41 = c^2
(after squaring)
C = 6.403
7.
Q. A right triangle has a hypotneuse of 13 and a leg of 8. What is the other leg? Show your work.
A.
13^2 - 8^2 = b^2
13^2 - 8^2 = b^2
169 64 = b^2
105 = b^2
(after squaring)
B = 10.246
8.
Q. A 12-foot ladder is leaning across a fence and is touching a higher wall located 3 feet behind the fence. The ladder makes an angle of 60 degrees with the ground. Find the distance from the base of the ladder to the bottom of the fence.
A.
NOTE: not sure exactly how to do this, I would appreciate a method on how to solve this one too.
cheers ![]()
#138 Re: Help Me ! » Special Right Triangles » 2013-07-28 13:56:25
So that means (sqrt3) x (sqrt12) = (sqrt36)
Square that and I get 6 which is answer B: 6
#19.
Answer is B: 6
#20.
Answer is D: 6.2414
#139 Re: Help Me ! » Special Right Triangles » 2013-07-25 05:31:25
#15.
9 divided by 3 = 3
and
3 x 3 = 9
So I will choose F: 3 sqrt3
#16.
I choose D: 6 sqrt3
#17.
I choose E: 3
#18.
I choose A: 1.7321
#19.
not too sure how to solve it with just a SQRT(12)
#140 Re: Help Me ! » Special Right Triangles » 2013-07-24 19:26:51
Yes I think that would be great if you could help out a little with those.
#141 Re: Help Me ! » Special Right Triangles » 2013-07-24 03:27:46
Alright I think I got the rest of them!
#6.
Answer is C: 4
#7.
Answer is B: 8
#8.
Now here is how I did this, tell me if I'm wrong/right:
SQRT(3) divided by 2 = SQRT1.5.
after squaring I get 1.224. Do I round off to the nearest which is answer A: 1.225?
#9
Answer is D: 3 sqrt2
#10
Answer is D: 84
#142 Re: Help Me ! » Special Right Triangles » 2013-07-24 02:21:38
Let me just do #6 to see if I got it right:
SQRT(8)
8 x 8 = 64
62 x 2 = 128
square 128 for 11.313 and round off to nearest number which will be A: 12. | Is this the correct way?
----
#10:
7sqrt(72) x 2 = 7(sqrt144).
7(sqrt144) = 7(12) = 7 x 12 = 84
Answer is 84... correct?
#143 Re: Help Me ! » Special Right Triangles » 2013-07-23 11:36:30
2.
The answer is going to be sqrt 3 I believe.
---
5.
6[SQRT(6)]
6 x 6 x 6 x 6 x 6 x 6 = 46656
(after squaring) 216
Cut in half for 108.
(after squaring) 10.3923
ANSWER: A - 6 sqrt(3) or 10.3923
#144 Help Me ! » Special Right Triangles » 2013-07-23 04:54:31
- demha
- Replies: 13
I'm not understanding too well. I would really appreciate an explanation. I answered what I could (which isn't much at all). All the ones I did not answer, I would really appreciate an explanation as to how to solve them.
If you have a 45-45-90 triangle:
1. And the length of one leg is 3, what is the length of the other leg? - Answer: A
A 3
B 6
C9
D12
E 15
F 18
2. With a hypotenuse of SQRT(6), what is the length of one leg?
A sqrt 81
Bsqrt 3
Csqrt 12
Dsqrt 23
E sqrt 37
F sqrt 42
3. And one leg has a length of 5, what is the length of the hypotenuse? - Answer: F
A 2sqrt3
B6sqrt4
C7sqrt9
D9sqrt7
E 4sqrt5
F 5sqrt2
4. With a hypotenuse of 7[SQRT(2)], what is the length of one leg? - Answer: 7
A 12
B94
C22
D7
E 45
F 2
5. With a hypotenuse of 6[SQRT(6)], what is the length of one leg?
A 6 sqrt(3) or 10.3923
B4 sqrt(10) or 9.3156
C3 sqrt(4) or 2.5631
D1 sqrt(5) or 3.5941
E 2 sqrt(9) or 8.2145
F 8 sqrt(7) or 6.2211
6. And one leg has a length of SQRT(8), what is the length of the hypotenuse?
A 12
B9
C4
D18
E 26
F 2
7. And one leg has a length of SQRT(32), what is the length of the hypotenuse?
A 24
B8
C46
D12
E 65
F 34
8. With a hypotenuse of SQRT(3), what is the length of one leg?
A 1.225
B2.189
C7.641
D1.218
E 4.321
F 1.657
9. With a hypotenuse of 6, what is the length of one leg?
A 11sqrt3
B4sqrt7
C7sqrt8
D3sqrt2
E 8sqrt9
F 2sqrt5
10. And one leg has a length of 7[SQRT(72)] what is the length of the hypotenuse?
A 04
B48
C91
D84
E 75
F 23
If you have a 30-60-90 triangle:
11. And the length of the shortest leg is 4, what's the length of the hypotenuse? - Answer: 8
A 5
B12
C20
D52
E 8
F 4
12. Working from #11, what's the length of the other leg? - Answer: 6 (i understand that is is 4(square root 3), 4 x 4 = 16, 16 x 3 = 48 then square root this to get the answer. is my method correct?)
A 3.0713
B4.1579
C9.2357
D6.9282
E 10.084
F 9.1157
13. And the length of the longest leg is 5[SQRT(3)], what's the length of the other leg? - Answer: E
A 2
B7
C16
D27
E 5
F 24
14. Working from #13, what's the length of the hypotenuse? - Answer: A
A 10
B24
C57
D91
E 39
F 46
15. And the length of the longest leg is 9, what is the length of shortest leg?
A 6sqrt5
B9sqrt2
C5sqrt6
D7sqrt5
E 4sqrt2
F 3sqrt3
16. Working from #15, what is the length of the hypotenuse?
A 2sqrt5
B3sqrt4
C8sqrt9
D6sqrt3
E 10sqrt2
F 7sqrt4
17. With a hypotenuse of 2[SQRT(3)] what is the length of the longest leg?
A 7
B33
C9
D27
E 3
F 14
18. Working from #17, what is the length of the shortest leg?
A 1.7321
B1.9443
C1.8459
D1.2946
E 1.0906
F 1.6504
19. And the length of the shortest leg is SQRT(12), what is the length of the longest leg?
A 29
B6
C38
D56
E 61
F 17
20. Working from #19, what is the length of the hypotenuse?
A 8.4197
B1.9764
C10.5742
D6.2414
E 2.4971
F 6.9282
#145 Re: Help Me ! » Trigonometry » 2013-07-17 04:07:28
I have an idea of how to do it. Not sure if it is exactly correct:
20/x = tan[30]
This gives me the answer of 36.64 which is answer F in #20.
#146 Re: Help Me ! » Trigonometry » 2013-07-16 15:11:17
After doing some research I figured it out!
15. Building 1 Angle 71o Distance 20 meters - i said F
A 89.26 m
B 74.23 m
C 25.62 m
D 19.23 m
E 67.23 m
F 58.08 m
16. Building 2 Angle 45o Distance 10 meters - i said D
A 4.13 m
B 8.73 m
C 25.62 m
D 10.00 m
E 5.46 m
F 58.08 m
17. Building 3 Angle 20o Distance 15 meters - i said E
A 4.13 m
B 8.73 m
C 25.62 m
D 10.00 m
E 5.46 m
F 58.08 m
18. Building 4 Angle 5o Distance 47.22 meters - i said A
A 4.13 m
B 8.73 m
C 25.62 m
D 10.00 m
E 5.46 m
F 58.08 m
19. Building 5 Angle 1o Distance 500 meters - I said B
A 4.13 m
B 8.73 m
C 25.62 m
D 10.00 m
E 5.46 m
F 58.08 m
~~~
For number 20, I am having a little trouble finding out how to figure this problem out. I could definitely use help on this.
20. You have climbed to the top of a tall tree. When you get to the top, you use your clinometer to discover that the angle between the tree and the line of sight to your red lunchbox is 30o. You know you left the lunchbox 20 meters from the base of the tree. How tall is the tree? (Careful! This is a little different than the building problems!)
A 75.36 m
B92.09 m
C20.17 m
D51.25 m
E 18.95 m
F 34.64 m
#147 Help Me ! » Trigonometry » 2013-07-16 14:42:33
- demha
- Replies: 5
I need a little help.
here is the question:
You have collected data on several buildings. For each building, you are given the angle of the line of sight up to the top of the building, and the distance to the building. Calculate the height of each building.
15. Building 1 Angle 71o Distance 20 meters
Now I know I can set it up either way:
tan71 = h/20
OR
h = 20tan71
I just don't have an idea as to how to solve it. I would really appreciate step by step help. There are more questions similar to this but, I want to know how to do this one so I can try to do the others.
#148 Re: Help Me ! » Geometry Review » 2013-06-25 06:55:33
Thanks guys!
#149 Re: Help Me ! » Geometry Review » 2013-06-24 10:33:05
7.
Would it be 2:1?
#150 Help Me ! » Geometry Review » 2013-06-24 03:42:13
- demha
- Replies: 11
So I just need help to make sure I got my answers right and there are also a few I was not too sure on how to do them, so help with those would be great ![]()
SO numbers 1 - 4 are referring to the image. It's only numbers 1 - 3 I'm not understanding too well on how to answer them. I would appreciate help with the first one (like a walk through) to help me understand. thanks! ![]()
REVIEW:
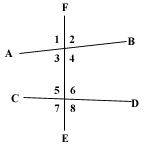
1.
Q. Refer to the image at the right. If angle 1 is 30 degrees, and angle 5 is 70 degrees, are the two lines parallel? Explain.
A.
2.
Q. Refer to the image at right. If angle 2 is 30 degrees and angle 4 is 60 degrees, are the lines parallel? Explain.
A.
3.
Q. Refer to the image at right. If angle 2 and angle 6 are both 70 degrees, are the lines parallel? Explain.
A.
4.
Q. Refer to the image at right. If the lines are parallel, and angle 4 is 50 degrees, what is the measure of angle 6?
A. Angle 6 will be 130 degrees.
5.
Q. What is the measure of the inner angle of a regular hexagon? Show your work (and be sure to explain anything you deem necessary to make sure your work is clear.)
A. A hexagon has 6 sides.
180 x 6 = 1080
The sum of the angles of deviation is 360
SO
1080 360 = 720
The final answer is 720
6.
Q. What is the measure of the inner angle of a regular decagon? Show your work (and be sure to explain anything you deem necessary to make sure your work is clear.)
A. A decagon has 10 sides.
180 x 10 = 1800
The sum of the angles of deviation is 360
SO
1800 360 = 1440
7.
Q. Polygon A has sides of 4, 3, 5, and 3. Polygon B has sides of 8, 6, 10, and 6. What are the two possible scale factors here? Explain.
A.
To get my scale factor, I will need to divide the two polygons. This is how I will do it along with the answers for each number:
4 / 8 = 1/2
3 / 6 = 1/2
5 / 10 = 1/2
3 / 6 = 1/2
So now we know the scale factor is 1:2.
8.
Q. A triangle has angles of 34 degrees, 56 degrees, and 90 degrees. It also have sides of 6, 8, and 10. Which side is across from which angle?
A.
Side 6 will be across angle 34.
Side 8 will be across angle 56.
Side 10 will be across angle 90.
9.
Q. A triangle has one angle measuring 52 degrees, and one angle measuring 18 degrees. What is the measure of the third angle?
A. The third angles measurement is 110 degrees.
10.
Q. A right triangle has a 90 degree angle, and an angle x. What will the measure of the third angle be?
A. I believe the answer for this would be 90 x.