Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#101 Re: Puzzles and Games » Calculus » 2016-02-17 05:30:00
Solve what?
#102 Re: Puzzles and Games » Perfect Squares » 2016-02-17 03:21:53
I was bored so I searched Anna's old posts for some more mentally challenging puzzles, and I found this. Allow me to present my solution.
Consider an integer x. If we add 30, then the result is a perfect square. If we subtract 30, the result is also a perfect square. How many such integers are there?"
So two perfect squares differ by 60. The difference between two perfect squares n² and (n+m)² is 2mn+m². Consider then all possible values of n and m such that 2mn+m²=60. NB: (i) Obviously m has to be even. (ii) We can also assume WLOG than both m and n are positive.
From here on 60−m², and hence n, will always be negative. Hence two are only three such integers, which are
[list=*]
[*]
[/*]
[/list]
#103 Re: Help Me ! » Summing » 2016-02-16 22:39:13
The fact is that the series 1+2+3+4+5+… diverges to +∞. Most of the statements in the mock proof don't make sense unless you take S = ∞ and treat infinity as a number (so you would have
[list=*]
[*]
[/list]
etc). Of course infinity isn't a number and people who don't know what they're doing should never treat it as a number. The above was only a mock proof of a mock statement – just an exercise in meaningless symbol manipulation.
#104 Re: Help Me ! » Summing » 2016-02-16 20:13:15
How about this?
Also
Substituting from [2]:
[1] + [3] ⇒
But we also have
Substituting [5] into [4]:
Finally
[6] & [7] ⇒
#105 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-16 19:06:02
#106 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-16 07:38:37
#107 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-16 01:04:37
#108 Re: Help Me ! » More Probability Help » 2016-02-15 23:20:38
Only #1 is correct.
#109 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-15 18:45:11
#110 Re: Help Me ! » More Probability Help » 2016-02-15 06:01:29
I will give you a hint for #1 and #2 (you already have a hint for #3). Given a batch of 1000 parts, 700 of them will be from Supplier A and 300 will be from Supplier B. Of the 700 from Supplier A, 14 will be defective, and of the 300 from Supplier B, 15 will be defective. So there will be 29 defective parts altogether. So...
#1. What's the probability of picking one of the 29 defective parts in a batch of 1000?
#2. Of the 29 defective parts, 14 are from Supplier A and 15 are from Supplier B. What is the probability of picking one of the 14 Supplier A parts from the defective bunch?
#111 Re: Help Me ! » Summing » 2016-02-14 23:17:05
How about the old division-by-zero trick?
#113 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-14 17:02:43
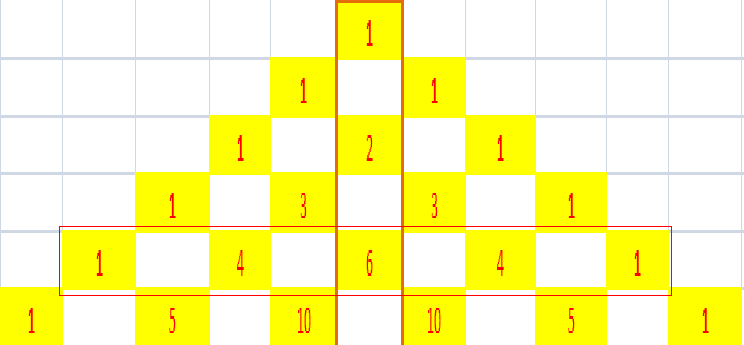
#114 Re: Help Me ! » A Pascal's Triangle Hidden Inside the Pascal's Triangle » 2016-02-13 23:11:50
On the subject of palindromic numbers, note the following:
[list=*]
[*]
[/list]
These are successive powers of n+1, where n is our base; they're palindromic up to some point depending on n. For base 10 (n=10) the palindromicity breaks down at the fifth power, when carrying-over starts to take over:
[list=*]
[*]
[/list]
To continue the palindromic sequence, all you need to do is choose a higher base (n>10). For example, consider the powers of 17 in hexadecimal:
[list=*]
[*]
[/list]
Ta da! Whereas (10+1)⁵ fails to be palindromic in base 10, (16+1)⁵ is palindromic in base 16. Choose n > 20 and (n+1)⁶ will be palindromic in base n too.
#115 Re: Help Me ! » A Pascal's Triangle Hidden Inside the Pascal's Triangle » 2016-02-13 22:41:58
I disagree with this statement from the website:
The same phenomenon appears where the row that bears the numbers 1-4-6-4-1 is the last palindromic sequence.
No, it is not! It is only the last because we are using base 10. If we use higher bases, the palindromic sequence will continue; e.g. in hexadecimal base, the next line would be 1-5-A-A-5-1; and in a still higher base (> 20) the next line would be 1-6-F-K-F-6-1. As you can see, any line in Pascal's triangle can be palindromic, if you choose a high-enough base.
As for the number 1001, it is of the form n³+1 = (n+1)(n²−n+1), where n is the base; hence it is composite regardless of the base chosen. If a number is composite, I'd say it has a good chance of appearing in Pascal's triangle.
Please help me make sense of my discovery because I`m not an expert mathematician as you. Thank you and warm regards.
All you need to know is that mathematics is always a very curious and interesting subject.
#116 Re: Help Me ! » Complex Number Problem » 2016-02-13 18:02:12
I have given you a big enough hint already!
Are you familiar with the fact that a complex number ζ is real if and only if it is equal to its complex conjugate, i.e.
[list=*]
[*]
[/list]?
#117 Re: Help Me ! » Skippy the kangaroo » 2016-02-12 20:38:31
The calculations in detail.
[list=*]
[*]
[/list]
Here f(n) is the number of ways Skippy can skip a distance of exactly n metres without moving backwards. If his initial skip is 1 metre, he has n−1 metres left to skip; if his starts by skipping 2 metres, he has n−2 metres left to do.
For backwardness:
[list=*]
[*]
[/list]
g(m) is the number of ways to get to the bowl from 7 metres away, skipping back a metre at the m-metre mark from the starting point. The kangaroo can skip the first m metres in f(m) ways; after the backward skip, he will be 8−m metres from his bowl, and can get there in f(8−m) ways.
Hence the total number of ways to skip to his bowl from 7 metres away (assuming he has the option to decline skipping backwards) is
[list=*]
[*]
[/list]
#118 Re: Help Me ! » Skippy the kangaroo » 2016-02-12 20:05:46
Why did you change your mind? I also got 167.
167 was for if Skippy could make 0 or 1 backward move. However, if Skippy has to make exactly 1 backward move, then 146. I wasn't sure what the wording of the puzzle meant.
I like Nehushtan's logic, but he left something out in both answers and included something in the first that gave the correct answer there.
What did I leave out? My logic is as follows.
First consider what happens when Skippy didn't make a backward move. To do 7 metres, he can skip 1 metre and then do 6 metres, or skip 2 metres and then do 5 metres. To do 6 metres, he can skip 1 metre and then do 5 metres, or skip 2 metres and then do 4 metres. And so on. So to compute how many ways to do 7 metres without moving backwards, I first compute the number of ways to do 1 and 2 metres 2, then 3 metres, then 4 metres, and so on, up to 7 metres. It turns out to be a case Fibonacci adding: if f(n) is the number of ways to do n metres, then:
[list=*]
[*]
[/list]
with f(1) = 1 and f(2) = 2.
Now for when Skippy can move backwards. He can do this when he's 1m, 2m, 3m, 4m, 5m or 6m from the starting point. Suppose he skips backwards at m metres from the starting point. He can do the first m metres in f(m) ways; after the backward skip, he has (8−m) metres left to do. Hence, if g(m) is the number of ways to get to the bowl skipping backwards at the m-metre mark, then
[list=*]
[*]
[/list]
where m = 1, 2, 3, 4, 5 or 6.
Hence the answer to the puzzle is
[list=*]
[*]
[/list]
This is assuming Skippy can choose not to skip backwards; if he has to make exactly one backward skip, then the answer is
[list=*]
[*]
[/list]
#119 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-12 19:33:14
#120 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-12 04:55:32
#121 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-12 04:48:04
#122 Re: Puzzles and Games » Arrange Mathematical Operation Using 0-9 to Match the Post Number » 2016-02-11 23:05:51
#123 Re: Help Me ! » Skippy the kangaroo » 2016-02-11 21:35:24
Sorry, change of mind.