Math Is Fun Forum

Hi bobbym,

I use the interval [-2,2] for both x and y, not for r and t.

Hi bobbym,

Thanks for your kind reply!

Below is an example function
f(r,t) = sin(mr)*cos(nt - pi) - (3/4)*cos(kt - pi/2) - r³ + 3r - 3/4.

The plotter I use to experiment is Graph 4.3. It transforms the coordinates and then
plots implicit rectangular equations. The plotter works fine if n, k are integers or
rational numbers with small denominators.

The plotting speed is very slow if n, k are irrational numbers or rational numbers
with large denominators (e.g. k = 3/128). And this is why I am looking for a plotter
which can plot implicit polar equations directly and quickly.

m=8, n=6, k=5: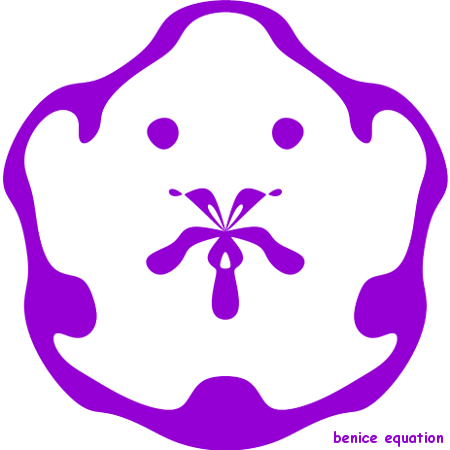

m=8, n=6, k=6:

Hi gAr,

Yes, those are all my posts. Thank you for giving this subject your attention.

        (Three different cross sections of the surface)

Hint:
Consider the intersection of a horizontal plane with the surface.

The intersection consists of a family of funny curves.
(An example curve is shown below. It has nothing to do with the answer.)

Cut off the upper surface above the horizontal plane
to get a funny 3D image.

(This curve is obtained from another surface.)

It's the graph of the following inequality:

[(x-1)^2 + y^2 - 4] [(x+1)^2 + y^2 - 4] [x^2 + (y - sqrt(3))^2 - 4] < c

c = 1, 12, 6