Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#101 Re: Help Me ! » Polygons and Review » 2013-09-16 05:39:30
Oh so it's 7/2 = 3.5, then
7 x 0.5 x 7 x 3.5/tan(25.71)
If this is correct, how would I solve it from here?
#102 Re: Help Me ! » Polygons and Review » 2013-09-16 02:17:54
5. A regular heptagon with a side of 7 inches.
A 178.06 sq in
B 294.16 sq in
C 169.21 sq in
D 358.91 sq in
E 157.36 sq in
F 277.91 sq in
360/7 = 51.42 => 25.71
3/tan(25.71)
7 x 0.5 x 7 x 3/tan(25.71)
Am I going the correct way with this? If so, how would I solve here? This is as far as I went:
24.5 x 3/tan(25.71)
---
19. What is the area of this rectangle?
Use Pythagoras to work out the height of the rectangle.
A 17.06 sq units
B 60 sq units
C 21.6 sq units
D 53 sq units
E 28.9 sq units
F 51 sq units z
H^2 = 13^2 - 12^2
H^2 = 169 - 144
H^2 = 25
H = 5
So now I know that Height = 5 and Base = 12, SO 5 x 12 = 60 sq units which is answer B.
#103 Re: Help Me ! » Polygons and Review » 2013-09-15 10:41:58
5. A regular heptagon with a side of 7 inches.
A 178.06 sq in
B 294.16 sq in
C 169.21 sq in
D 358.91 sq in
E 157.36 sq in
F 277.91 sq in
I'm having a hard time understanding how to solve this and #17. Do you think you could create a similar math problem and then show me how to solve it step by step? For example maybe you can do the same as #5, except with a side of 5 instead of 7 inches.
---
17. What is the area of a regular octagon with a side of 6 cm?
A 178.06 sq cm
B 122.5 sq cm
C 216 sq cm
D 23 cm^2
E 173.82 cm^2
F 510 cm^2
Same as #5.
---
19. What is the area of this rectangle?
Use Pythagoras to work out the height of the rectangle.
A 17.06 sq units
B 60 sq units
C 21.6 sq units
D 53 sq units
E 28.9 sq units
F 51 sq units z
H^2 = 13^2 - 12^2
H^2 = 169 - 144
H^2 = 25
H = 5
Not too sure what I did wrong here.
20. What is the area of this polygon?
My picture below shows how you can split this shape into a rectangle and a triangle. You will also need to use Pythag. to get the length of the red line.
A 178 sq units
B 129 sq units
C 230 sq units
D 240 sq units
E 219 sq units
F 206 sq units
Ok so the rectangle area is 152 and the triangle area is 54. Add them together to get 206 which will be the answer: F - 206 sq units.
#104 Re: Help Me ! » Polygons and Review » 2013-09-14 22:12:18
Thank you for your reply Bob and yes, your assumption is correct, we are looking for the area here. I will begin with 5:
5. A regular heptagon with a side of 7 inches. ***need help understanding how to solve***
A 178.06 sq in
B 294.16 sq in
C 169.21 sq in
D 358.91 sq in
E 157.36 sq in
F 277.91 sq in
360/7 = 51.42 (central angle)
51.42/2 = 25.71 | 25.71tan = 0.48
51.42 x 0.48 = 24.6768 x 7 = 172.7712
I'm not understanding what went wrong here.
---
16. What is the area of a parallelogram with height 26 cm, base 16 cm, and side length 28 cm?
A 178.06 sq cm
B 122.5 sq cm
C 216 sq cm
D 416 cm^2
E 28.9 cm
F 510 cm^2
Makes sense! Answer is D - 416 cm^2
17. What is the area of a regular octagon with a side of 6 cm? ***need help understanding how to solve***
A 178.06 sq cm
B 122.5 sq cm
C 216 sq cm
D 23 cm^2
E 173.82 cm^2
F 510 cm^2
360/8 = 45
half it so 45/2 = 22.5
Am I right so far? If so, would the next step be 22.5tan?
18. What is the area of this polygon?***need help understanding how to solve***
You can split this polygon onto three rectangles. (see picture below) You will have to use the information to work out the length and width of each part and then add up the areas.
ls_XF = 53 mm ls_XV = 72 mm ls_VR = 16 mm
ls_FB = 31 mm ls_BT = 31 mm ls_EU = 47 mm
ls_UL = 31 mm ls_TL = 88 mm ls_DE = 16 mm
ls_RM = 70 mm ls_MC = 21 mm ls_DC = 70 mm
A 8014 mm2
B7030 mm2
C6027 mm2
D5478 mm2
E 1782 mm2
F 1225 mm2
Takes a little while but got the answer: A - 8014 mm2
19. What is the area of this rectangle?***need help understanding how to solve***
Use Pythagoras to work out the height of the rectangle.
A 17.06 sq units
B60 sq units
C21.6 sq units
D53 sq units
E 28.9 sq units
F 51 sq units
So this is the equation I started with: H^2 = 13^2 - 12^2
Am I starting right?
20. What is the area of this polygon?***need help understanding how to solve***
My picture below shows how you can split this shape into a rectangle and a triangle. You will also need to use Pythag. to get the length of the red line.
A 178 sq units
B129 sq units
C230 sq units
D240 sq units
E 219 sq units
F 206 sq units
Not exactly sure where to start on this.
#105 Help Me ! » Polygons and Review » 2013-09-14 13:37:02
- demha
- Replies: 35
Just need some help understanding some of these math problems and checking the ones I already did (if right/wrong). Thank you for your time:
1. An equilateral triangle with a side of 1 inch - Answer: A
A 0.43 sq in
B 0.56 sq in
C 0.89 sq in
D 0.23 sq in
E 0.19 sq in
F 0.54 sq in
2. A square with a side of 2 feet - Answer: B
A 9 sq ft
B 4 sq ft
C 2 sq ft
D 7 sq ft
E 3 sq ft
F 8 sq ft
3. A regular pentagon with a side of 3 centimeters - Answer: F
A 23.01 sq cm
B 12.34 sq cm
C 39.17 sq cm
D 9.46 sq cm
E 34.21 sq cm
F 15.48 sq cm
4. A regular hexagon with a side of 10 cm - Answer: D
A 641.25 sq cm
B 194.45 sq cm
C 361.25 sq cm
D 259.81 sq cm
E 105.22 sq cm
F 453.01 sq cm
5. A regular heptagon with a side of 7 inches. ***need help understanding how to solve***
A 178.06 sq in
B 294.16 sq in
C 169.21 sq in
D 358.91 sq in
E 157.36 sq in
F 277.91 sq in
6. A trapezoid where the height is 18 cm, base 1 = 16 cm and b2 = 8 cm. - Answer: C
A 178.06 sq cm
B 122.5 sq cm
C 216 sq cm
D 230 sq cm
E 280.9 sq cm
F 510 sq cm
7. A trapezoid where the height = 7 mm, base 1 = 26 mm and base 2 = 9 mm. - Answer: B
A 178.06 sq mm
B 122.5 sq mm
C 216 sq mm
D 230 sq mm
E 28.9 mm
F 510 mm
Fill in the missing information for the following trapezoids:
8.
height = 19.8 cm
b1 = ________
b2 = 14.4 cm
area = 401.94 cm2 - Answer: A
A 26.2 cm
B 12.5 cm
C 216 cm
D 23 cm
E 28.9 cm
F 51 cm
9.
height = 23 mm
b1 = 23 mm
b2 = ________
area = 529 mm2 - Answer: D
A 78.06 sq mm
B 22.5 sq mm
C 21.6 mm
D 23 mm
E 28.9 mm
F 30 mm^2
10.
height = ________
b1 = 20 cm
b2 = 21 cm
area = 205 cm2 - Answer: D
A 17.06 cm
B 12.5 sq cm
C 26 cm
D 10 cm
E 28.9 cm
F 50 cm^2
11.
height = 28.9 m
b1 = 26.9 m
b2 = ________
area = 806.31 m^2 - Answer: E
A 17.06 sq m
B 15 m
C 46 m
D 23 m
E 28.9 m
F 51 m
12. If the area of a parallelogram is 690.84 m^2 and the height is 20.2 m, what is the length of the base? - Answer: D
A 78.06 m
B 22.5 m
C 216 m
D 34.2 m
E 28.9 m
F 51 m
13. If the base of a rectangle is 28 cm and the area is 588 cm^2, what is the height of the rectangle? - Answer: E
A 17.06 cm
B 122.5 sq cm
C 216 sq cm
D 23 cm
E 21 cm
F 51 cm^2
14. If the height of a rectangle is 26.1 m and the base is 17.3 m, what is the area of the rectangle? - Answer: A
A 451.53 m^2
B 122.5 m^2
C 216 m^2
D 430 m^2
E 289 m^2
F 510 m^2
15. If the height of a parallelogram is 34 cm and the base is 15 cm, what is the area of the parallelogram? - Answer: F
A 178.06 cm^2
B 122.5 cm^2
C 216 cm^2
D 230 cm^2
E 289 cm^2
F 510 cm^2
16. What is the area of a parallelogram with height 26 cm, base 16 cm, and side length 28 cm?***need help understanding how to solve***
A 178.06 sq cm
B 122.5 sq cm
C 216 sq cm
D 416 cm^2
E 28.9 cm
F 510 cm^2
17. What is the area of a regular octagon with a side of 6 cm? ***need help understanding how to solve***
A 178.06 sq cm
B 122.5 sq cm
C 216 sq cm
D 23 cm^2
E 173.82 cm^2
F 510 cm^2
18. What is the area of this polygon?***need help understanding how to solve***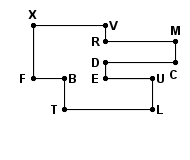
ls_XF = 53 mm ls_XV = 72 mm ls_VR = 16 mm
ls_FB = 31 mm ls_BT = 31 mm ls_EU = 47 mm
ls_UL = 31 mm ls_TL = 88 mm ls_DE = 16 mm
ls_RM = 70 mm ls_MC = 21 mm ls_DC = 70 mm
A 8014 mm2
B7030 mm2
C6027 mm2
D5478 mm2
E 1782 mm2
F 1225 mm2
19. What is the area of this rectangle?***need help understanding how to solve***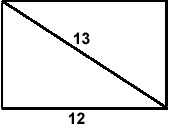
A 17.06 sq units
B60 sq units
C21.6 sq units
D53 sq units
E 28.9 sq units
F 51 sq units
20. What is the area of this polygon?***need help understanding how to solve***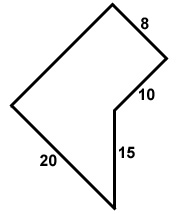
A 178 sq units
B129 sq units
C230 sq units
D240 sq units
E 219 sq units
F 206 sq units
#106 Re: Help Me ! » Math Review » 2013-09-13 02:59:48
Finished with this lesson! Thank you very much Bobbym for your help. Much appreciated!!
#107 Re: Help Me ! » Math Review » 2013-09-12 07:32:13
So I'm guessing I went wrong some where, but where?
#108 Re: Help Me ! » Math Review » 2013-09-12 05:13:38
Ok here is the "redo" for #7 - #10:
7. When the rope goes around the barn, what is the new radius? How much of a circle can it make without hitting the barn or overlapping area you've already found? What is that area?
Answer: The new radius is 30. It can make up to ¼. So the area would be:
1/4 x 30^2 x PI
1/4 x 900 x PI
225 (PI) = 706.858
8. When the rope goes around the barn the other way, what is the new radius? How much of a circle can it make without hitting the barn or overlapping area you've already found? What is that area?
Answer: The radius is 30. It can make up to ¼. So the area would be:
1/4 x 30^2 x PI
1/4 x 900 x PI
225 (PI) = 706.858
9. The areas you found in 7 and 8 overlap each other. How much do they overlap? What *approximate* shape do they make? What is that area?
Answer: I would say that the area is 75. It looks like it almost makes a square shape.
10. What is the total grazing area the goat can reach?
Answer: To get this answer, I added up the ansers of #6, #7 and #8 then subtracted the answer from #9:
1875(PI) + 225(PI) + 225(PI) 75
2325(PI) 75
7304.202 75
7229.202 is the final answer.
#109 Re: Help Me ! » Math Review » 2013-09-12 02:52:47
Ok, so redoing #7 - #9:
7. When the rope goes around the barn, what is the new radius? How much of a circle can it make without hitting the barn or overlapping area you've already found? What is that area?
Answer:
1/4 x 30^2 x PI
1/4 x 900 x PI
225 (PI)
8. When the rope goes around the barn the other way, what is the new radius? How much of a circle can it make without hitting the barn or overlapping area you've already found? What is that area?
Answer: (this would be the same as #7)
1/4 x 30^2 x PI
1/4 x 900 x PI
225 (PI)
9. The areas you found in 7 and 8 overlap each other. How much do they overlap? What *approximate* shape do they make? What is that area?
Answer:
3/4 x 10^2 x PI
3/4 x 100 x PI
75 (PI)
---
If these are right, shall we move on to #10?
#110 Re: Help Me ! » Math Review » 2013-09-12 00:28:00
Cool! So it would be:
3/4 x 10^2 x PI
3/4 x 100 x PI
75 (PI) is the final answer or 235.619
And #7 and #8 are literally asking for the same thing. So the equation for them both would be:
1/4 x 30^2 x PI
1/4 x 900 x PI
225 (PI) is the final answer or 706.858 - is this correct?
#111 Re: Help Me ! » Math Review » 2013-09-11 14:15:39
3/4 x 10^2 x PI
This would be the equation for #9?
#112 Re: Help Me ! » Math Review » 2013-09-11 11:35:17
Yes I understand that. The E-circle represents the entire range, the F-circle and G-circle represent the both ways the goat can go, and the H-circle (green) represents where they overlap. So would this just be considered as one area, as in just 10? Making the equation:
1/4 x 10^2 x PI
Am I following the right path here?
#113 Re: Help Me ! » Math Review » 2013-09-11 09:01:55
To me it looks as if each side is over lapping by 3 blocks, each side overlapping by a green and two reds. Would that mean they are overlapping by 30? (3 blocks, each block = 10, 3 x 10 = 30)
#114 Re: Help Me ! » Math Review » 2013-09-11 05:08:35
Yes I keep getting mixed up so sorry! The rope goes around the barn 3/4. But I have been thinking that #7 and #8 will be the same equation:
3/4 x 30^2 x PI
I know there is 10 left but that is what we can use for #9? It asks "The areas you found in 7 and 8 overlap each other. How much do they overlap? What *approximate* shape do they make? What is that area?" So I came to believe that the equation for THIS number will be:
1/4 x 10^2 x PI
Am I right on this?
#115 Re: Help Me ! » Math Review » 2013-09-11 04:54:35
So I would do the equation with 10? As in:
1/4 x 10^2 x PI
#116 Re: Help Me ! » Math Review » 2013-09-11 04:50:11
Can we use the image for #6 to #10?

#117 Re: Help Me ! » Math Review » 2013-09-11 04:41:56
I'm really confused here right now >_<
#118 Re: Help Me ! » Math Review » 2013-09-11 04:24:21
Yes, and then there will be 10 feet left just enough to get around another corner.
#119 Re: Help Me ! » Math Review » 2013-09-11 04:18:17
#7:
When the rope goes around the barn, what is the new radius? How much of a circle can it make without hitting the barn or overlapping area you've already found? What is that area?
I believe they are asking for the first turn because in #8 they say " When the rope goes around the barn the other way",
#120 Re: Help Me ! » Math Review » 2013-09-11 04:11:31
So I add them together to get 40 THEN do the equation?
#121 Re: Help Me ! » Math Review » 2013-09-11 04:07:41
#7
How would i do this one?
#122 Re: Help Me ! » Math Review » 2013-09-11 03:39:59
That's great to hear! What about 7 & 8?
#123 Re: Help Me ! » Math Review » 2013-09-11 03:08:28
Yes they all are.
#124 Re: Help Me ! » Math Review » 2013-09-11 02:52:33
Somewhat, I kind of drew one on paper and based it on that. #9 and #10 i am finding a little difficult to find the answer.
#125 Re: Help Me ! » Math Review » 2013-09-11 02:23:13
And thank you Bobbym for your help on Post #1!