Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
#51 Re: Help Me ! » Finding numbers if LCM is given. » 2015-04-04 03:08:40
What about 15,15 or 30,30?
#52 Re: Help Me ! » Linear Differential Equations » 2015-04-04 02:27:36
Do you know why we have to choose e^(something) for these, why no other solutions are possible
and also why the general solution is c1.(a particular solution) + c2.(another particular solution)?
#53 Re: Maths Is Fun - Suggestions and Comments » Happy Easter!!! » 2015-04-04 00:33:20
Happy Easter, everyone!
#54 Re: Help Me ! » Linear Differential Equations » 2015-04-03 04:27:09
Let
[list=*]
[*]
[/list]
and suppose
[list=*]
[*]
[/list]
for some v ≠ 0. Then
[list=*]
[*]
[/list]
Since the LHS is zero for some x, y not both zero, the determinant of the matrix on the LHS must be 0.
Note that eigenvalues can be complex.
#56 Re: Puzzles and Games » Mathemagic » 2015-03-31 22:06:00
The most general theorem of all:
(NB: If N contains one or more 0, we allow Nʹ to start with a 0. For example, if N = 1024, Nʹ can be 0241; in this case N is a 4-digit number whereas Nʹ = 241 is a 3-digit one.)
Proof of the most general theorem of all:
We know that a positive integer is congruent modulo 9 to the sum of its digits. For example, 12345 ≡ 1+2+3+4+5 = 15 ≡ 1+5 = 6 (mod 9) (i.e. it leaves a remainder 6 when divided by 9).
This is based on the fact that is divisible by 9 for all non-negative integers k (these are numbers of the form 0, 9, 99, 999, 9999, etc). Therefore if N is a k-digit number with digits , we have[list=*]
[*]
[/list]
and adding up the i gives
So N is congruent to the sum of its digits mod 9. Similarly Nʹ is congruent to the sum of its digits mod 9. But the sum of the digits of N and the sum of the digits of Nʹ are the same since the digits of one are those of the other rearranged. This means
[list=*]
[*]
[/list]
and so their difference is divisible by 9. QED.
#57 Re: Help Me ! » Floor functions » 2015-03-31 20:06:19
Why did you guys remove {x}
Sorry, it was a typo. I've put it back in post #9.
#58 Re: Help Me ! » Floor functions » 2015-03-31 03:43:42
Strictly, as you have one thing ≥ x and another ≥ 0, when you add them you get (one thing + another) ≥ x
No, I have the first thing > x and the other ≥ 0.
#59 Re: Help Me ! » Floor functions » 2015-03-31 00:03:58
Okay, this should work. For all x,
[list=*]
[*]
[/list] because .
Also, for all x,
[list=*]
[*]
[/list]
(Fractional parts cannot be neagative.)
for all x.Is this better, Bob? ![]()
#60 Re: Help Me ! » Floor functions » 2015-03-30 23:42:20
Oops, I did it wrong. ![]()
Back to the drawing board.
#61 Re: Help Me ! » Floor functions » 2015-03-30 21:24:01
Here's an algebraic proof. For all x,
[list=*]
[*]
[/list]
#62 Re: Help Me ! » Floor functions » 2015-03-30 20:39:36
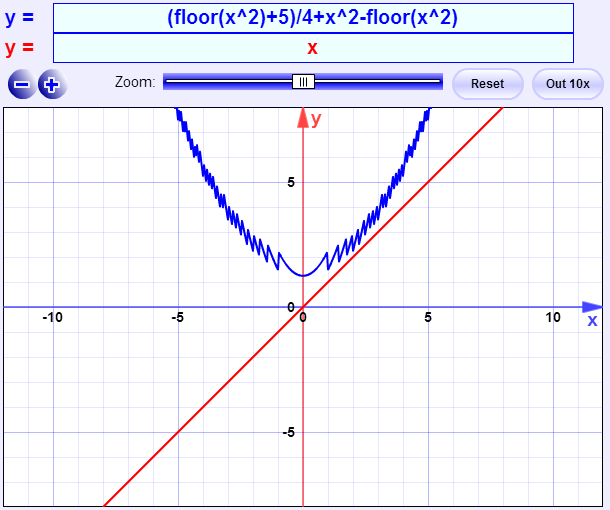
No solution.
#63 Re: Jokes » Some more clean jokes! » 2015-03-29 19:13:07
"So, Peter, you've finally come to believe in the existence of the fourth dimension of reality."
"Yes, Paul, it's about time."
#64 Re: Maths Teaching Resources » Brilliant Mathematics and Science Wikis » 2015-03-29 00:31:57
Is there a section on group theory or abstract algebra? Or algebraic topology?
#65 Re: Jokes » One Liners » 2015-03-28 08:01:52
San Andreas should be blamed for all the earthquake activity in California because it's his fault.
#68 Re: Help Me ! » conics » 2015-03-25 22:57:17
Oh! Thank you Bob, I forgot about the tan formula. ![]()
#69 Re: Help Me ! » conics » 2015-03-25 21:26:41
[list=*]
[*]
[/list]
Implicit differentiation gives
[list=*]
[*]
[/list] at P.
Hence the angle between the two tangents is
[list=*]
[*]
[/list]
PS: It's actually
[list=*]
[*]
[/list]
since the gradient to the curve will always be steeper than the gradient to the circle.
#71 Re: Puzzles and Games » Mate in three? » 2015-03-23 04:45:51
This is a much more interesting puzzle than I thought. If indeed all variations end with mate in three, it must have taken a super genius brain to work them out, given there were no computers in the 19th century. I can see why it won first prize. ![]()
#72 Re: Puzzles and Games » Janes cryptic crossword clues » 2015-03-23 00:56:36
#26. Having a will of one's own? (7)
#73 Re: Puzzles and Games » Mate in three? » 2015-03-23 00:53:18
Oh, I didn't see that. Thanks, SteveB.
#74 Puzzles and Games » Mate in three? » 2015-03-22 22:34:34
- Olinguito
- Replies: 19
This is a chess problem from The Illustrated London News, a 19th-century publication. According to the author it is possible for white to mate in three moves but I can't find a solution. ![]()
[list=*]
[*] [/*]
[/*]
[/list]
The best I can do is I analysed the problem at http://www.chesslab.com/PositionSearch.html but it couldn't find a mate-in-three either; however it did find an
Can anyone find a mate in three, if there is one? Phrontister? ![]()
#75 Re: Puzzles and Games » Janes cryptic crossword clues » 2015-03-16 21:50:23
I think the last one should be
#23. Legal heir will cut up ginger. (4,9)
#24. Stick insect and mammal. (7, 3)
#25. Seriousness is what can pull you down. (7)